Что такое выборочное распределение?

Представьте себе, что существует популяция из 10 000 дельфинов, и средний вес дельфина в этой популяции составляет 300 фунтов.

Если мы возьмем простую случайную выборку из 50 дельфинов из этой популяции, мы можем обнаружить, что средний вес дельфинов в этой выборке составляет 305 фунтов.

Затем, если мы возьмем еще одну простую случайную выборку из 50 дельфинов, мы можем обнаружить, что средний вес дельфинов в этой выборке составляет 295 фунтов.

Всякий раз, когда мы берем простую случайную выборку из 50 дельфинов, вполне вероятно, что средний вес дельфинов в выборке близок к среднему по популяции 300 фунтам, но не точно 300 фунтам.

Давайте представим, что мы берем 200 простых случайных выборок по 50 дельфинов из этой популяции и создаем гистограмму среднего веса каждой выборки:

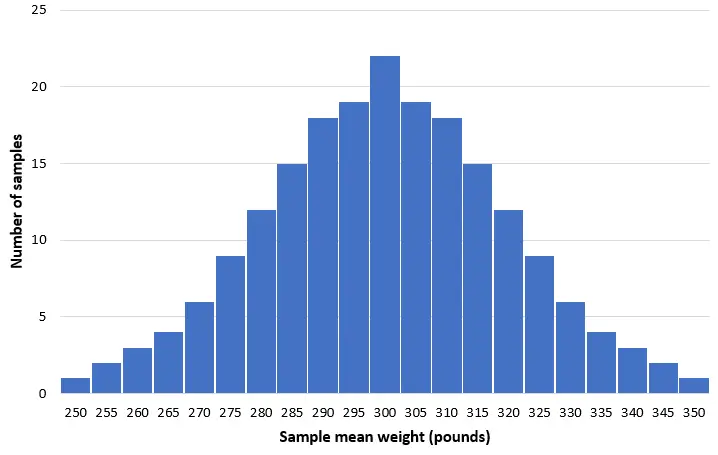
В большинстве образцов средний вес будет близок к 300 фунтам. В редких случаях мы можем взять в выборку маленьких дельфинов, средний вес которых составляет всего 250 фунтов. Или мы могли бы взять образец, полный дельфинов-афалин, средний вес которых составляет 350 фунтов. В целом распределение выборочных средних будет примерно нормальным, с центром распределения, расположенным в истинном центре генеральной совокупности.

Такое распределение выборочных средних известно как выборочное распределение среднего и имеет следующие свойства:

_хх = ц

где μ _x — выборочное среднее, а μ — среднее по генеральной совокупности.

_σx = σ/√n

где σ _x — стандартное отклонение выборки, σ — стандартное отклонение генеральной совокупности, а n — размер выборки.

Например, мы знаем, что в этой популяции дельфинов средний вес равен ц = 300. Таким образом, среднее значение выборочного распределения составляет ц _х = 300 .

Предположим, мы также знаем, что стандартное отклонение населения составляет 18 фунтов. Таким образом, стандартное отклонение выборки составляет σ _x = 18/ √50 = 2,546 .

Выборочное распределение доли

Рассмотрим ту же популяцию из 10 000 дельфинов. Предположим, 10% дельфинов черные, а остальные серые. Предположим, мы возьмем простую случайную выборку из 50 дельфинов и обнаружим, что 14% дельфинов в этой выборке черные. Затем мы берем еще одну простую случайную выборку из 50 дельфинов и обнаруживаем, что 8% дельфинов в этой выборке черные.

Представьте, что мы берем 200 простых случайных выборок по 50 дельфинов из этой популяции и создаем гистограмму доли черных дельфинов в каждой выборке:

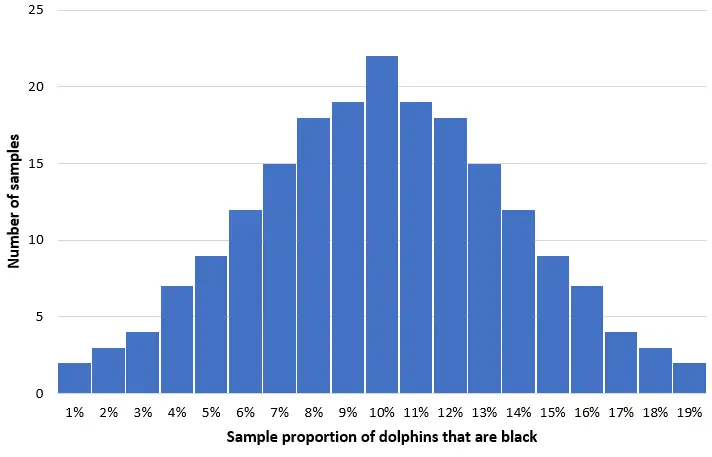
В большинстве выборок доля черных дельфинов будет близка к фактической популяции в 10%. Распределение выборочной доли черных дельфинов будет примерно нормальным, с центром распределения, расположенным в истинном центре популяции.

Такое распределение выборочных долей известно как выборочное распределение долей и обладает следующими свойствами:

_µp = P

где p — доля выборки, а P — доля населения.

σ _p = √ (P)(1-P)/n

где P — доля населения, а n — размер выборки.

Например, мы знаем, что в этой популяции дельфинов истинная доля черных дельфинов составляет 10% = 0,1. Таким образом, среднее значение выборочного распределения пропорциональности составляет µ _p = 0,1 .

Предположим, мы также знаем, что стандартное отклонение населения составляет 18 фунтов. Таким образом, стандартное отклонение выборки составляет σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Установить нормальность

Чтобы использовать приведенные выше формулы, распределение выборки должно быть нормальным.

Согласно центральной предельной теореме , выборочное распределение выборочного среднего является приблизительно нормальным, если размер выборки достаточно велик, даже если распределение совокупности не является нормальным . В большинстве случаев мы считаем размер выборки в 30 и более достаточно большим.

Выборочное распределение доли выборки является примерно нормальным, если ожидаемое количество успешных и неудачных попыток не менее 10.

Примеры

Мы можем использовать выборочные распределения для расчета вероятностей.

Пример 1: Определенная машина создает файлы cookie. Распределение веса этих файлов cookie смещено вправо со средним значением 10 унций и стандартным отклонением 2 унции. Если мы возьмем простую случайную выборку из 100 штук печенья, произведенных этой машиной, какова вероятность того, что средний вес печенья в этой выборке составит менее 9,8 унций?

Шаг 1: Установите нормальную жизнь.

Нам необходимо убедиться, что распределение выборочных средних является нормальным. Поскольку размер нашей выборки больше или равен 30, в соответствии с центральной предельной теоремой мы можем предположить, что выборочное распределение выборочных средних является нормальным.

Шаг 2: Найдите среднее и стандартное отклонение выборочного распределения.

_хх = ц

_σx = σ/√n

мкм _х = 10 унций

σ _x = 2/ √100 = 2/10 = 0,2 унции

Шаг 3. Используйте калькулятор площади Z-показателя , чтобы определить вероятность того, что средний вес печенья в этом образце составит менее 9,8 унций.

Введите следующие числа в калькулятор площади Z-оценки. Вы можете оставить поле «Необработанный балл 2» пустым, поскольку в этом примере мы находим только одно число.

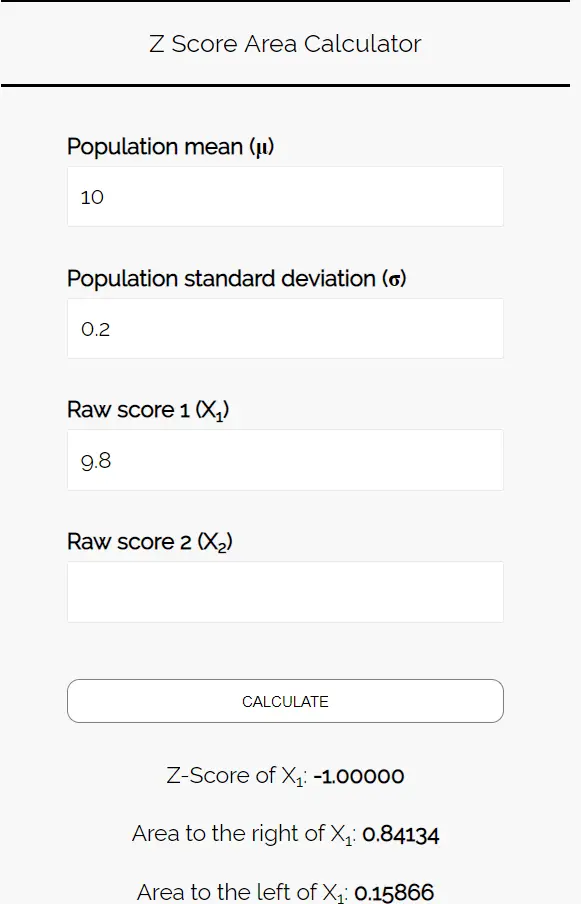
Поскольку мы хотим узнать вероятность того, что средний вес печенья в этом образце будет меньше 9,8 унций, нас интересует область слева от 9,8. Калькулятор сообщает нам, что эта вероятность равна 0,15866 .

Пример 2: Согласно общешкольному исследованию, 87% учеников конкретной школы предпочитают пиццу мороженому. Предположим, мы возьмем простую случайную выборку из 200 студентов. Какова вероятность того, что доля студентов, предпочитающих пиццу, составит менее 85%?

Шаг 1: Установите нормальную жизнь.

Напомним, что выборочное распределение доли выборки является примерно нормальным, если ожидаемое количество «успехов» и «неуспехов» не менее 10.

В этом случае ожидаемое количество студентов, которые предпочтут пиццу, составит 87% * 200 студентов = 174 студента. Ожидаемое количество студентов, которые не предпочтут пиццу, составляет 13% * 200 студентов = 26 студентов. Поскольку оба этих числа не меньше 10, можно предположить, что выборочное распределение доли студентов, которые предпочтут пиццу, примерно нормальное.

Шаг 2: Найдите среднее и стандартное отклонение выборочного распределения.

_µp = P

σ _p = √ (P)(1-P)/n

_цп = 0,87

σ _р = √ (0,87)(1-0,87)/200 = 0,024

Шаг 3. Используйте калькулятор площади Z-показателя , чтобы определить вероятность того, что доля учащихся, предпочитающих пиццу, составляет менее 85%.

Введите следующие числа в калькулятор площади Z-оценки. Вы можете оставить поле «Необработанный балл 2» пустым, поскольку в этом примере мы находим только одно число.

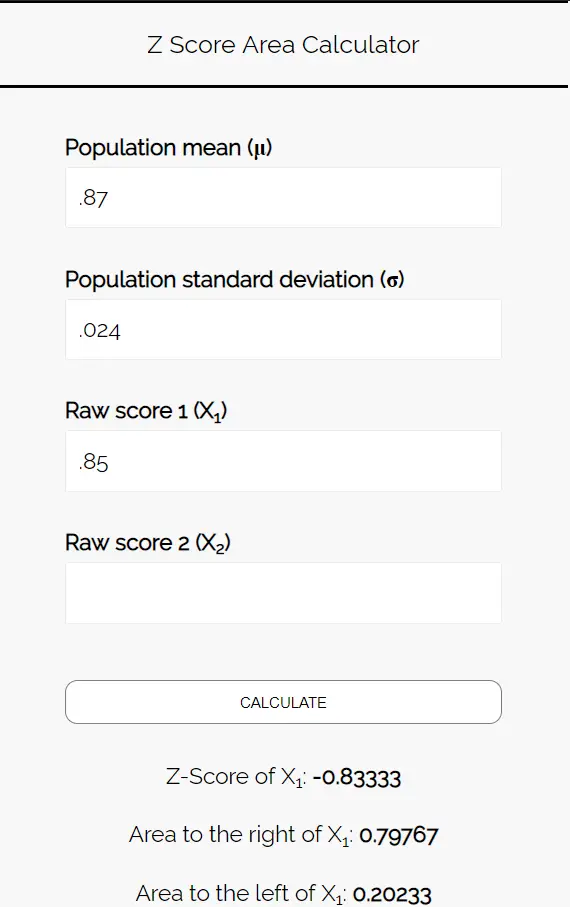
Поскольку мы хотим знать вероятность того, что доля студентов, предпочитающих пиццу, составляет менее 85%, нас интересует область слева от 0,85. Калькулятор сообщает нам, что эта вероятность равна 0,20233 .