Выборочное распределение разницы средних

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое выборочное распределение разницы между двумя средними значениями в статистике. Вы также найдете формулу выборочного распределения разницы средних и, кроме того, пошаговое решение упражнения.

Каково выборочное распределение разницы средних?

Выборочное распределение разницы средних значений — это распределение, которое получается в результате расчета различий между средними значениями всех возможных выборок из двух разных популяций.

То есть, чтобы получить выборочное распределение разницы средних значений, необходимо выбрать все возможные выборки из двух исследуемых популяций, затем рассчитать среднее значение каждой выбранной выборки и, наконец, разницу между всеми средними значениями, рассчитанными из двух популяций. Таким образом, набор значений, полученных после применения всех этих операций, образует выборочное распределение разницы средних.

Разница распределения выборки средних значений используется для расчета вероятности того, что разница между двумя средними значениями случайно выбранных выборок из двух разных популяций близка к разнице средних значений генеральной совокупности.

➤ См.: Выборочное распределение среднего значения.

Формула выборочного распределения разницы средних значений

Если размер выборки достаточно велик (n ₁ ≥30 и n ₂ ≥30), выборочное распределение разницы средних значений соответствует нормальному распределению. Точнее, параметры указанного распределения рассчитываются следующим образом:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Примечание. Если обе совокупности имеют нормальное распределение , то выборочное распределение разницы средних значений следует нормальному распределению независимо от размеров выборки.

Следовательно, поскольку выборочное распределение разницы средних значений определяется нормальным распределением, формула для расчета статистики выборочного распределения разницы средних значений имеет вид:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Золото:

$\overline{x_i}$

является средним значением выборки i.
$\mu_i$

является средним значением численности населения i.
$\sigma_i$

— стандартное отклонение генеральной совокупности i.
$n_i$

размер выборки i.
$Z$

— переменная, определяемая стандартным нормальным распределением N(0,1).

Обратите внимание, что выборки из разных групп населения могут иметь разные размеры выборки.

Конкретный пример выборочного распределения разницы средних

Как только мы увидим определение разницы среднего выборочного распределения и ее формулу, мы увидим пошаговый пример, чтобы завершить понимание концепции разницы среднего выборочного распределения.

В статистическом исследовании мы хотим проанализировать разницу между ростом мальчиков и девочек определенного возраста. Мы знаем, что распределение, определяющее популяцию мальчиков этого возраста, имеет среднее значение 157 см и стандартное отклонение 9 см, а с другой стороны, распределение, определяющее популяцию девочек этого возраста, имеет среднее значение 148. см и стандартное отклонение 7 см. Если выбрана выборка из 30 мальчиков этого возраста и выборка из 35 девочек этого возраста, какова вероятность того, что средний рост выборки мальчиков на 12 см больше, чем средний рост выборки девочек?

Чтобы решить эту проблему, первое, что нужно сделать, это вычислить статистику разницы средних выборочных распределений. Поэтому мы применяем формулу, показанную выше:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48$

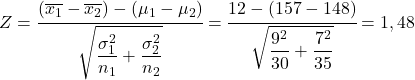
Следовательно, вероятность того, что средний рост мальчиков в выборке на 12 см превышает средний рост девочек, эквивалентна вероятности того, что переменная Z больше 1,48.

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]» title=»Rendered by QuickLaTeX.com» height=»19″ width=»253″ style=»vertical-align: -5px;»></p> </p> <p> Поэтому мы ищем вероятность Z>1,48 в <a href=$ таблице Z :

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=»Rendered by QuickLaTeX.com» height=»19″ width=»331″ style=»vertical-align: -5px;»></p> </p> <p> Короче говоря, вероятность того, что средний рост мальчиков в выборке на 12 см больше, чем средний рост девочек, составляет 6,94%.</p> </div>  <div class=$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Каково выборочное распределение разницы средних?

Формула выборочного распределения разницы средних значений

Конкретный пример выборочного распределения разницы средних

Об авторе

бенджамин андерсон

Добавить комментарий