Введение в геометрическое распределение
Геометрическое распределение описывает вероятность испытать определенное количество неудач до первого успеха в серии испытаний Бернулли.
Испытание Бернулли — это эксперимент только с двумя возможными исходами — «успех» или «неудача» — и вероятность успеха одинакова каждый раз, когда проводится эксперимент.
Примером эссе Бернулли является подбрасывание монеты. Монета может упасть только на два орла (мы могли бы назвать орла «попаданием», а решку — «провалом»), и вероятность успеха при каждом подбрасывании равна 0,5, если предположить, что монета честная.
Если случайная величина X подчиняется геометрическому распределению, то вероятность возникновения k неудач до первого успеха можно найти по следующей формуле:
P(X=k) = (1-p) kp
Золото:
- k: количество неудач до первого успеха
- p: вероятность успеха в каждом испытании
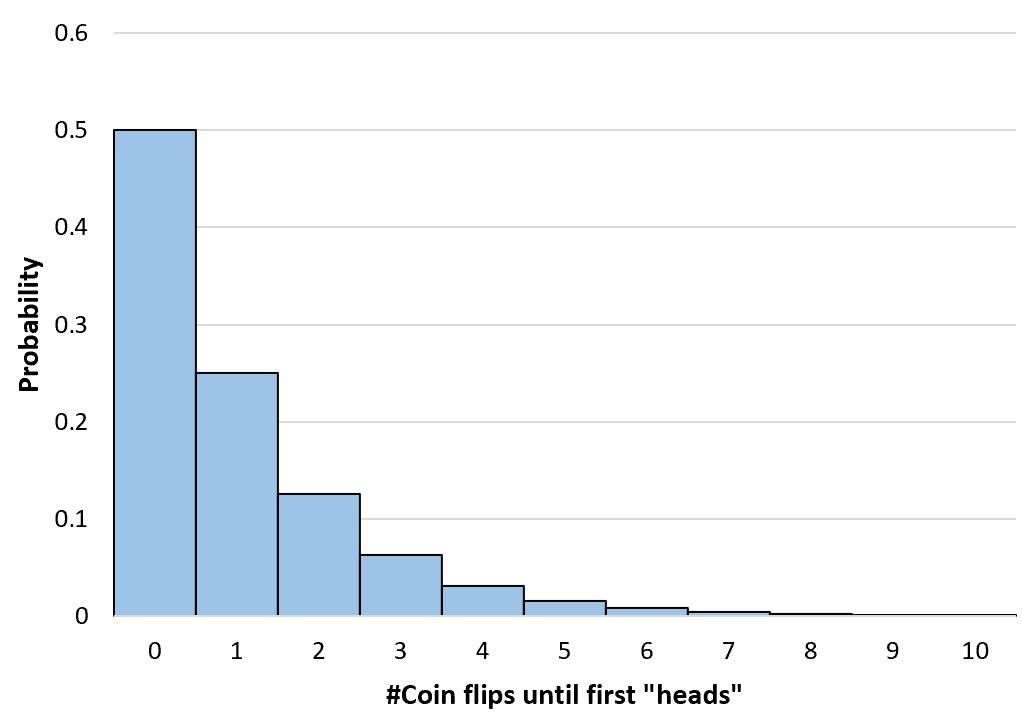
Например, предположим, что мы хотим знать, сколько раз нам придется подбросить честную монету, пока не выпадет орел. Мы можем использовать приведенную выше формулу, чтобы определить вероятность возникновения 0, 1, 2, 3 сбоев и т. д. прежде чем монета упадет на решку:
Примечание: монета может испытать 0 «провалов», если при первом броске выпадет орел.
P(X=0) = (1-.5) 0 (.5) = 0.5
P(X=1) = (1-.5) 1 (.5) = 0.25
P(X=2) = (1-.5) 2 (.5) = 0.125
Р(Х=3) = (1-0,5) 3 (0,5) = 0,0625
Мы можем вычислить вероятность любого количества бросков монеты до бесконечности. Затем мы создаем простую гистограмму для визуализации этого распределения вероятностей:
Расчет совокупных геометрических вероятностей
Совокупную вероятность того, что мы испытаем k или меньше неудач до первого успеха, можно найти по следующей формуле:
P(X≤k) = 1 – (1-p) k+1
Золото:
- k: количество неудач до первого успеха
- p: вероятность успеха в каждом испытании
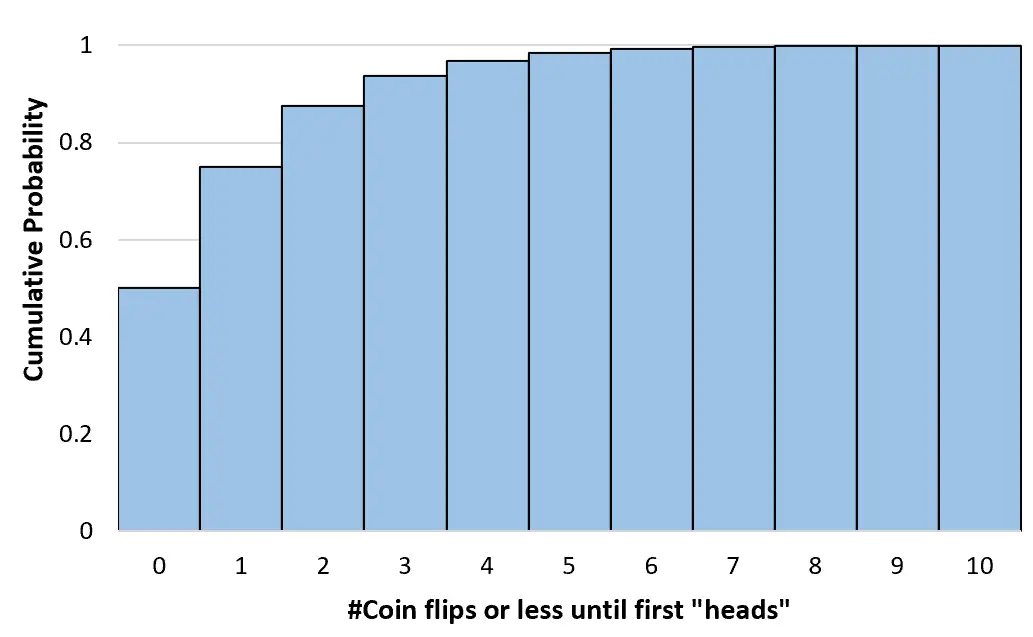
Например, предположим, что мы хотим узнать вероятность того, что потребуется три или меньше «промахов», прежде чем монета наконец упадет орлом. Для расчета этой вероятности мы будем использовать следующую формулу:
P(X≤3) = 1 – (1-0,5) 3+1 = 0,9375
Мы можем вычислить каждую кумулятивную вероятность, используя аналогичную формулу:
P(X≤0) = 1 – (1-.5) 0+1 = 0.5
P(X≤1) = 1 – (1-0,5) 1+1 = 0,75
P(X≤2) = 1 – (1-0,5) 2+1 = 0,875
Мы можем вычислить эти совокупные вероятности для любого количества бросков монеты, вплоть до бесконечности. Затем мы можем создать гистограмму для визуализации этого кумулятивного распределения вероятностей:
Свойства геометрического распределения
Геометрическое распределение обладает следующими свойствами:
Среднее значение распределения равно (1-p)/p .
Дисперсия распределения равна (1-p)/p 2 .
Например:
Среднее количество раз, когда мы ожидаем, что монета упадет орел до того, как упадет решка, будет (1-p) / p = (1-.5) / .5 = 1 .
Дисперсия количества бросков до выпадения орла будет равна (1-p)/ p2 = (1-.5)/. 52 = 2 .
Практические задачи геометрического распределения
Используйте следующие практические задачи, чтобы проверить свои знания о геометрическом распределении.
Примечание. Для расчета ответов на эти вопросы мы воспользуемся калькулятором геометрического распределения .
Проблема 1
Вопрос: Исследователь ждет возле библиотеки, чтобы спросить людей, поддерживают ли они определенный закон. Вероятность того, что данный человек поддерживает закон, равна p = 0,2. Какова вероятность того, что четвертый человек, с которым беседует исследователь, первым поддержит закон?
Ответ: Число «неуспехов» до первого успеха – то есть количество людей, которые не поддерживают закон до тех пор, пока его не поддержит первый человек – равно 3. Итак, при использовании калькулятора геометрического распределения с p = 0,2 и x = 3 отказа, мы находим, что P(X=3) = 0,10240 .
Проблема 2
Вопрос: Исследователь ждет возле библиотеки, чтобы спросить людей, поддерживают ли они определенный закон. Вероятность того, что данный человек поддерживает закон, равна p = 0,2. Какова вероятность того, что исследователю придется поговорить более чем с четырьмя людьми, чтобы найти кого-то, кто поддерживает закон?
Ответ: Используя калькулятор геометрического распределения при p =0,2 и x = 4 отказах, находим, что P(X>4) = 0,32768 .
Проблема 3
Вопрос: Исследователь ждет возле библиотеки, чтобы спросить людей, поддерживают ли они определенный закон. Вероятность того, что данный человек поддерживает закон, равна p = 0,2. С каким ожидаемым количеством людей придется поговорить исследователю, пока он не найдет человека, поддерживающего закон?
Ответ: Напомним, что среднее геометрическое распределение равно (1-p)/p . В этой ситуации среднее значение будет (1-.2)/.2 = 4 .