Дискретное равномерное распределение

К бенджамин андерсон 3 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое дискретное равномерное распределение и какова его характеристическая формула. Аналогичным образом вы сможете увидеть графическое представление дискретного равномерного распределения и его свойства.

Что такое дискретное равномерное распределение?

Дискретное равномерное распределение — это дискретное распределение вероятностей, в котором все значения равновероятны, то есть в дискретном равномерном распределении все значения имеют одинаковую вероятность появления.

Например, бросок игральной кости можно определить с помощью дискретного равномерного распределения, поскольку все возможные исходы (1, 2, 3, 4, 5 или 6) имеют одинаковую вероятность выпадения.

В общем, дискретное равномерное распределение имеет два характерных параметра a и b , которые определяют диапазон возможных значений, которые может принимать распределение. Таким образом, когда переменная определяется дискретным равномерным распределением, она пишется Uniform(a,b) .

Дискретное равномерное распределение можно использовать для описания случайных экспериментов, поскольку, если все результаты имеют одинаковую вероятность, это означает, что эксперимент является случайным.

Формула дискретного равномерного распределения

Теперь, когда мы знаем определение дискретного равномерного распределения, мы увидим, какая формула позволяет рассчитать вероятность появления значений распределения этого типа.

Функция вероятности дискретного равномерного распределения постоянна и ее значение равно единице по общему числу возможных исходов. Таким образом, формула дискретного равномерного распределения имеет следующий вид:

$P[X=x]=\cfrac{1}{n}=\cfrac{1}{b-a+1}$

С другой стороны, формула кумулятивной функции вероятности дискретного равномерного распределения выглядит следующим образом:

$P[X\leq x]=\cfrac{\lfloor x \rfloor -a + 1}{b-a+1}$

Золото

$a$

$b$

– характерные параметры дискретного равномерного распределения.

Дискретная диаграмма равномерного распределения

Поскольку дискретное равномерное распределение может принимать только определенные значения в интервале, его графическое представление состоит из точек. Более того, все вероятности равны, поэтому все точки дискретного равномерного распределения имеют одну и ту же вертикальную координату.

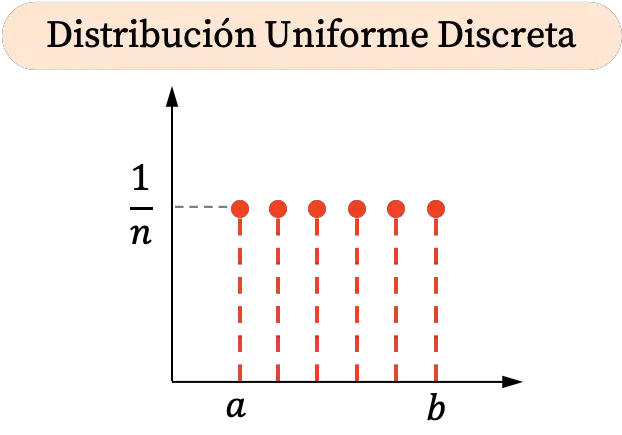
С другой стороны, график кумулятивной вероятности дискретного равномерного распределения выглядит следующим образом:

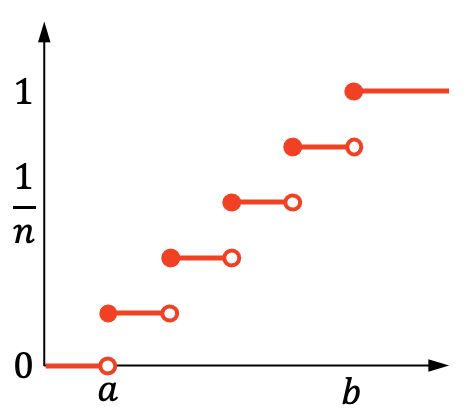
кумулятивная вероятность дискретного равномерного распределения

Характеристики дискретного равномерного распределения

Дискретное равномерное распределение имеет следующие характеристики:

Дискретное равномерное распределение определяется двумя целочисленными параметрами a и b , которые определяют диапазон возможных значений распределения.

$\begin{array}{c} X\sim \text{Uniforme}(a,b)\\[2ex]b\geq a\\[2ex]n=b-a+1\end{array}$

Среднее значение дискретного равномерного распределения равно сумме двух его характеристических параметров, разделенной на два.

$E[X]=\cfrac{a+b}{2}$

Медиана дискретного равномерного распределения эквивалентна его среднему значению, поэтому рассчитывается с помощью того же выражения:

$Me=\cfrac{a+b}{2}$

Дисперсия дискретного равномерного распределения равна квадрату общего количества исходов минус один, разделенному на двенадцать.

$Var(X)=\cfrac{n^2-1}{12}$

Дискретное равномерное распределение симметрично относительно своего среднего значения, поэтому коэффициент асимметрии этого распределения вероятностей равен нулю.

$A=0$

Эксцесс дискретного равномерного распределения можно рассчитать с помощью следующего выражения:

$C=-\cfrac{6\cdot (n^2+1)}{5\cdot (n^2+1)}$

Дискретное равномерное распределение и непрерывное равномерное распределение

Наконец, мы увидим, в чем разница между дискретным равномерным распределением и непрерывным равномерным распределением, поскольку это два похожих типа распределения вероятностей, но с существенной разницей.

Разница между дискретным равномерным распределением и непрерывным равномерным распределением заключается в их возможных значениях. Дискретное равномерное распределение может принимать только определенные значения в интервале, тогда как непрерывное равномерное распределение может принимать любое значение в интервале, в котором оно определено.

В общем, дискретные равномерные распределения могут принимать только целые значения, тогда как непрерывные равномерные распределения также могут принимать десятичные значения.

➤ См.: Непрерывное равномерное распределение.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше