Дисперсия

К бенджамин андерсон 5 августа, 2023 Статистика 0 комментариев

В этой статье мы объясним, что такое дисперсия, также называемая дисперсией, и как она рассчитывается. Вы найдете формулу дисперсии, конкретный пример расчета дисперсии, а также сможете посчитать дисперсию любого набора данных с помощью онлайн-калькулятора.

Мы также покажем вам, как найти дисперсию сгруппированных данных, поскольку это делается другим способом. Наконец, мы научим вас разнице между генеральной дисперсией и выборочной дисперсией, разнице между дисперсией и стандартным отклонением, а также свойствам этой статистической меры.

Что такое дисперсия?

В статистике дисперсия — это мера дисперсии, которая указывает на изменчивость случайной величины. Дисперсия равна сумме квадратов остатков, деленной на общее количество наблюдений.

Имейте в виду, что под остатком понимается разница между значением точки статистических данных и средним значением набора данных.

В теории вероятностей символом дисперсии является греческая буква сигма в квадрате (σ ² ). Хотя его также обычно представляют как Var(X) , где X является случайной величиной, по которой рассчитывается дисперсия.

В общем, интерпретировать значение дисперсии случайной величины просто. Чем больше значение дисперсии, тем более разбросаны данные. И наоборот, чем меньше значение дисперсии, тем меньше будет дисперсия в ряду данных. Однако при интерпретации дисперсии следует быть осторожным с выбросами , поскольку они могут исказить значение дисперсии.

дисперсия, другими мерами, которые считаются помимо дисперсии, являются диапазон, стандартное отклонение, среднее отклонение и коэффициент вариации.

Как рассчитать зазор

Для расчета дисперсии необходимо выполнить следующие действия:

Найдите среднее арифметическое набора данных.
Рассчитайте остатки, определяемые как разница между значениями и средним значением набора данных.
Возведите каждый остаток в квадрат.
Добавьте все результаты, рассчитанные на предыдущем шаге.
Разделите на общее количество данных. Полученный результат представляет собой дисперсию ряда данных.

В заключение формула для расчета дисперсии набора данных:

Золото:

$X$

— случайная величина, для которой вы хотите вычислить дисперсию.
$x_i$

значение данных

$i$

.
$n$

общее количество наблюдений.
$\overline{X}$

среднее значение случайной величины

$X$

.

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать дисперсию любого набора данных.

Следовательно, чтобы извлечь дисперсию из ряда данных, важно знать, как рассчитывается среднее арифметическое. Если вы не помните, как это сделать, вы можете проверить это в статье, указанной выше.

Пример отклонения

Теперь, когда мы знаем определение дисперсии, мы шаг за шагом решим упражнение, чтобы вы могли увидеть, как получается дисперсия ряда данных.

От транснациональной компании известен экономический результат, который она имела за последние пять лет, в большинстве своем она получила прибыль, но за один год принесла значительные убытки: 11,5, 2, -9, 7 миллионов евро. Рассчитайте дисперсию этого набора данных.

Как мы видели в объяснении выше, первое, что нам нужно сделать, чтобы найти дисперсию ряда данных, — это вычислить его среднее арифметическое:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

И как только мы узнаем среднее значение данных, мы можем использовать формулу дисперсии:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

Подставляем данные, предоставленные оператором исполнения, в формулу:

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

Наконец, остается только решить операции по вычислению дисперсии:

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

Обратите внимание, что единицы дисперсии — это те же самые единицы статистических данных, но в квадрате, поэтому дисперсия этой группы данных составляет 45,76 миллиона евро ² .

Калькулятор разрыва

Введите набор статистических данных в следующий калькулятор, чтобы рассчитать его дисперсию. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Отклонение для сгруппированных данных

Для расчета дисперсии данных, сгруппированных по интервалам , необходимо выполнить следующие шаги:

Найдите среднее значение сгруппированных данных.
Вычислите остатки сгруппированных данных.
Возведите каждый остаток в квадрат.
Умножьте каждый предыдущий результат на частоту его интервала.
Сложите сумму всех значений, полученных на предыдущем шаге.
Разделите на общее количество наблюдений. Полученное число представляет собой дисперсию сгруппированных данных.

Другими словами, формула расчета дисперсии данных, сгруппированных по интервалам, выглядит следующим образом:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

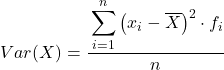
Хотя обычно используется приведенная выше формула, можно также использовать приведенное ниже алгебраическое выражение, поскольку оно эквивалентно:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

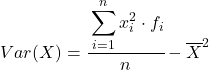
В качестве примера мы найдем дисперсию следующего сгруппированного ряда данных:

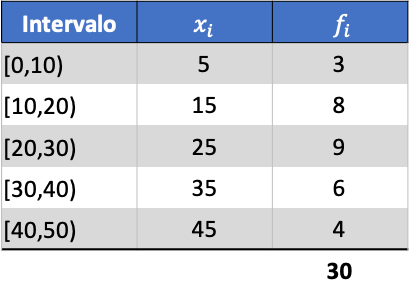
Во-первых, нам нужно определить среднее значение сгруппированных данных. Для этого добавим в таблицу частот столбец с произведением марки класса и частоты:

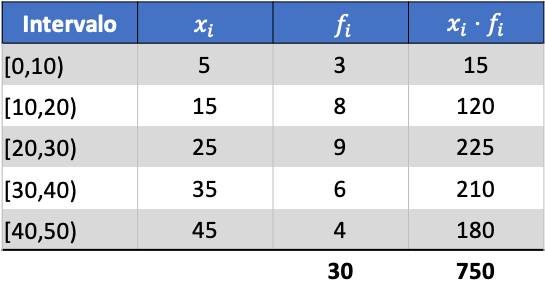
данные сгруппированы по среднему значению

Теперь мы вычисляем среднее значение сгруппированных данных, разделив сумму добавленного столбца на общее количество данных:

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

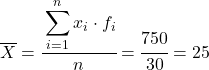
И к среднему значению рассчитанных данных мы можем добавить следующие три столбца:

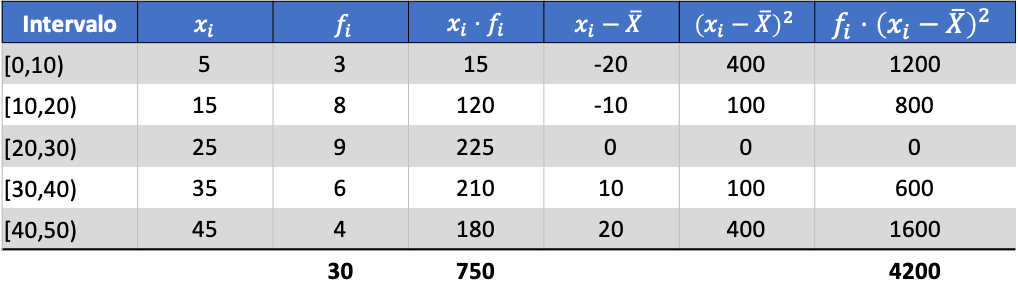
Таким образом, дисперсия объединенного набора данных представляет собой сумму последнего столбца, разделенную на общее количество наблюдаемых данных:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

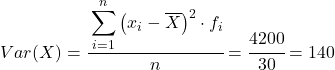
Дисперсия и стандартное отклонение

Дисперсия и стандартное отклонение (или стандартное отклонение) являются двумя мерами дисперсии и, следовательно, обе указывают степень дисперсии набора данных. Однако разница между дисперсией и стандартным отклонением заключается в том, что обычно дисперсия имеет большие значения, поскольку она представляет собой квадрат стандартного отклонения.

Стандартное отклонение обычно обозначается греческой буквой «сигма» (σ), и по этой причине дисперсия обозначается буквой «сигма в квадрате» (σ ² ), поскольку между этими двумя показателями дисперсии существует математическая связь.

$Var(X)=\sigma^2$

Итак, после того, как вы вычислили значение дисперсии набора данных, вы можете легко найти значение стандартного отклонения того же набора, просто извлекая квадратный корень из дисперсии.

$\sigma=\sqrt{\sigma^2}$

Дисперсия генеральной совокупности и выборочная дисперсия

Логично, что дисперсия совокупности относится к расчету дисперсии статистической совокупности, а вместо этого дисперсия выборки применяется к расчету дисперсии выборки. Однако это две разные концепции, поскольку формула генеральной дисперсии отличается от формулы выборочной дисперсии.

Обычно в упражнениях на дисперсию, если нам не говорят иначе, чтобы найти дисперсию предоставленного набора данных, мы должны использовать формулу дисперсии совокупности , которую мы объяснили в начале статьи:

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

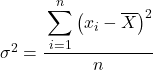
Но, возможно, в некоторых задачах вас просят рассматривать статистические данные как выборку, и в этом случае нам нужно использовать формулу выборочной дисперсии :

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

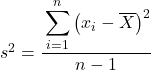
Обратите внимание: чтобы указать, что рассчитывается дисперсия генеральной совокупности, она обозначается греческой буквой σ, но когда рассчитывается выборочная дисперсия, используется буква s.

Как видите, единственная разница между двумя формулами заключается в том, что дисперсию выборки нам нужно разделить на общее количество наблюдений минус 1, например, если всего элементов данных 30, мы разделим на 29. Но вычисление числителя производится точно так же.

Свойства отклонения

Дисперсия обладает следующими свойствами:

Дисперсия любой случайной величины всегда будет больше или равна нулю. Аналогично, если дисперсия равна нулю, это означает, что все статистические данные одинаковы.

$Var(x)\ge 0$

Очевидно, что дисперсия одного значения равна нулю.

$Var(a)=0\qquad a\in \mathbb{R}$

Дисперсия произведения скаляра на переменную эквивалентна квадрату скаляра, умноженному на дисперсию переменной.

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

Дисперсия суммы двух зависимых переменных эквивалентна сумме дисперсии каждой переменной в отдельности плюс удвоенная ковариация между двумя переменными.

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

Следовательно, если две переменные независимы, для определения дисперсии их суммы достаточно сложить их дисперсии:

$Var(X+Y)=Var(X)+Var(Y)$

Отклонение также можно определить с помощью математического ожидания по следующей формуле:

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше