Что такое дихотомические переменные? (определение & #038; пример)

Дихотомическая переменная — это тип переменной, которая принимает только два возможных значения.

Вот несколько примеров дихотомических переменных:

• Пол: мужской или женский
• Подбрасывание монеты: орел или решка
• Тип недвижимости: Жилая или Коммерческая
• Статус спортсмена: профессионал или любитель.
• Результаты экзамена: сдать или не сдать

На практике переменные такого типа возникают постоянно. Например, рассмотрим следующий набор данных, который содержит 10 наблюдений и 4 переменные:

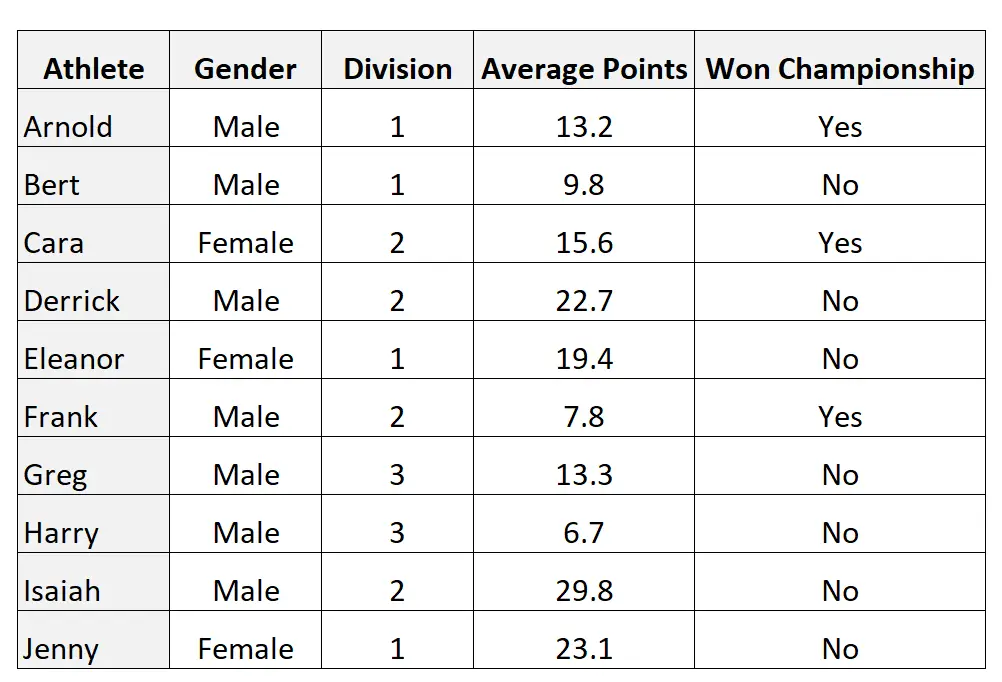
Переменные «пол» и «Выигранный чемпионат» являются дихотомическими, поскольку каждая из них может принимать только два возможных значения:

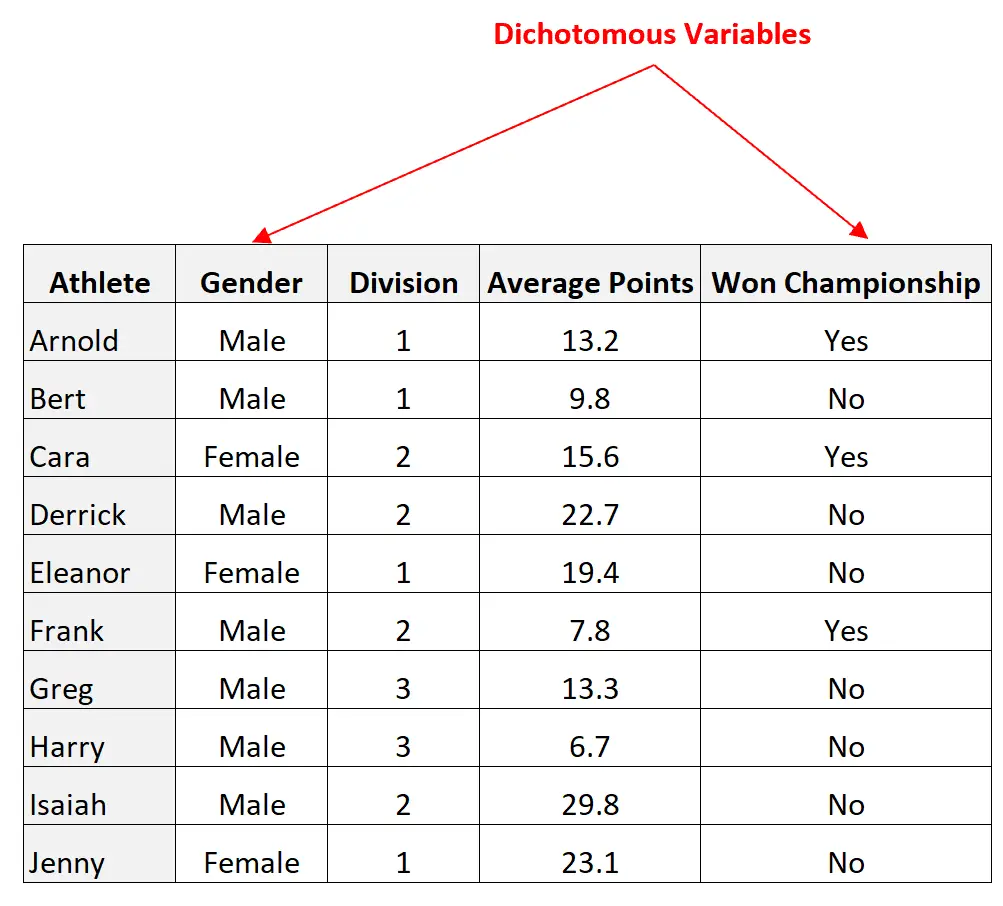
Однако переменные Division и Average Points не являются дихотомическими, поскольку они могут принимать несколько значений.

Бонусный совет:

Вы можете помнить, что дихотомические переменные могут принимать только два значения, помня, что префикс «ди» — это греческое слово, означающее «два», «дважды» или «двойной».

Как создавать дихотомические переменные

Следует отметить, что мы можем создать дихотомическую переменную из непрерывной переменной, просто разделив значения на основе определенного порога.

Например, в предыдущем наборе данных мы могли бы преобразовать переменную «Среднее количество очков» в дихотомическую переменную, классифицируя игроков со средним баллом выше 15 как «хороших бомбардиров», а игроков со средним баллом ниже 15 — как «плохих бомбардиров»:

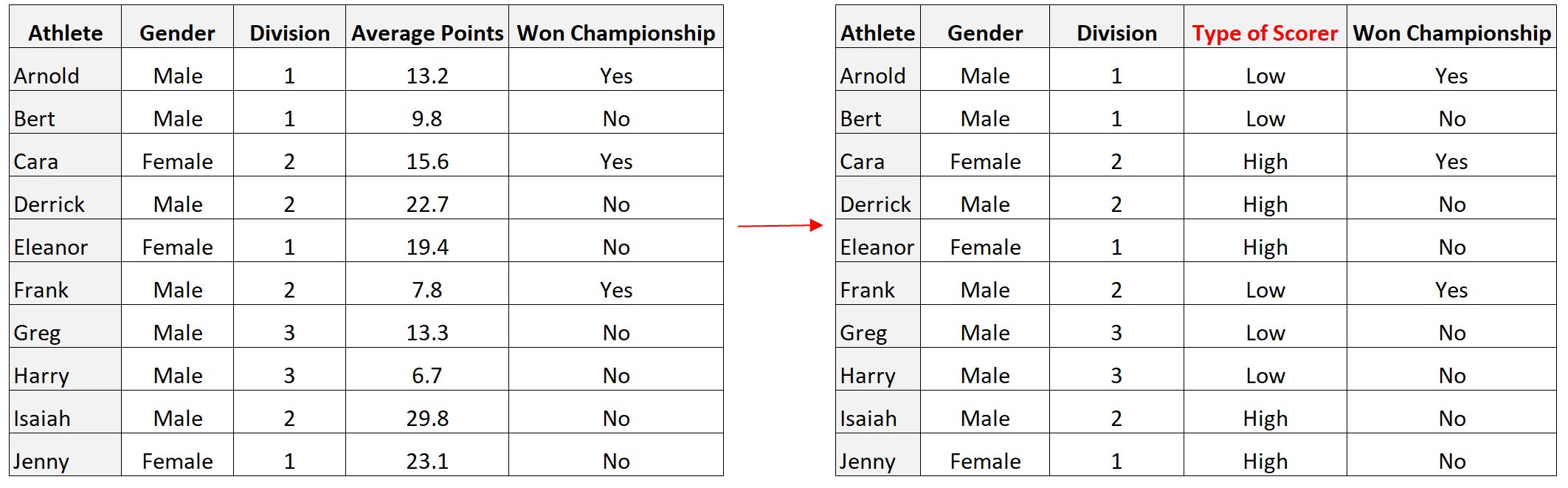
Как визуализировать дихотомические переменные

Обычно мы визуализируем дихотомические переменные, используя простую гистограмму, чтобы представить частоты каждого значения, которое они могут принимать.

Например, на следующей гистограмме показаны частоты каждого пола в предыдущем наборе данных:

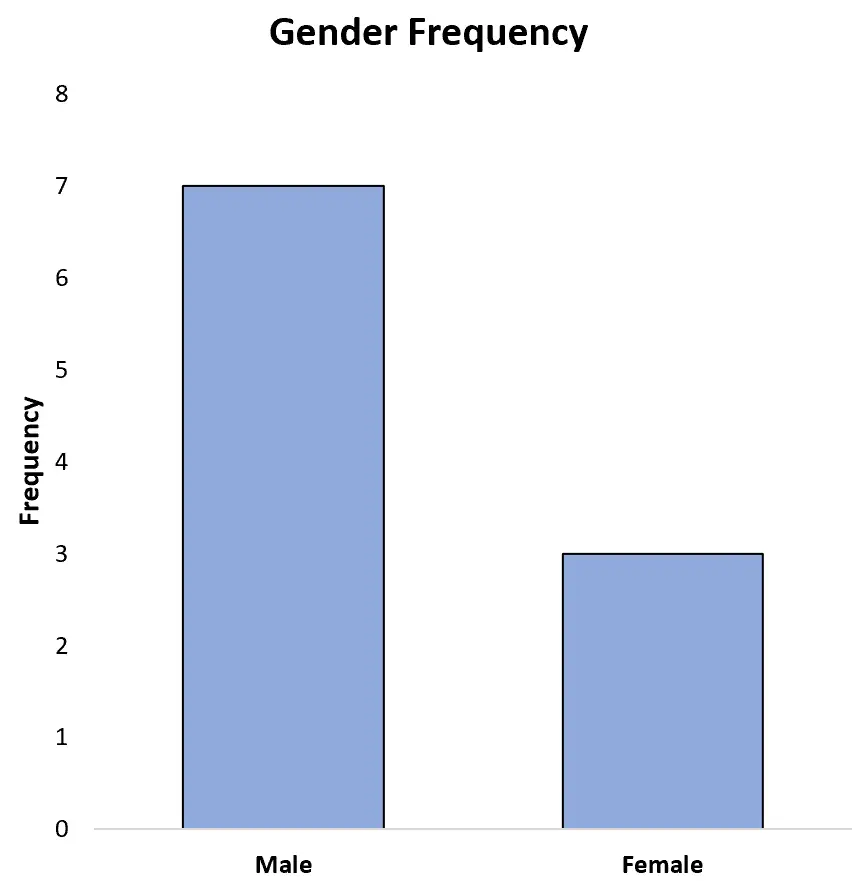
Мы также могли бы отображать частоты в процентах по оси Y:

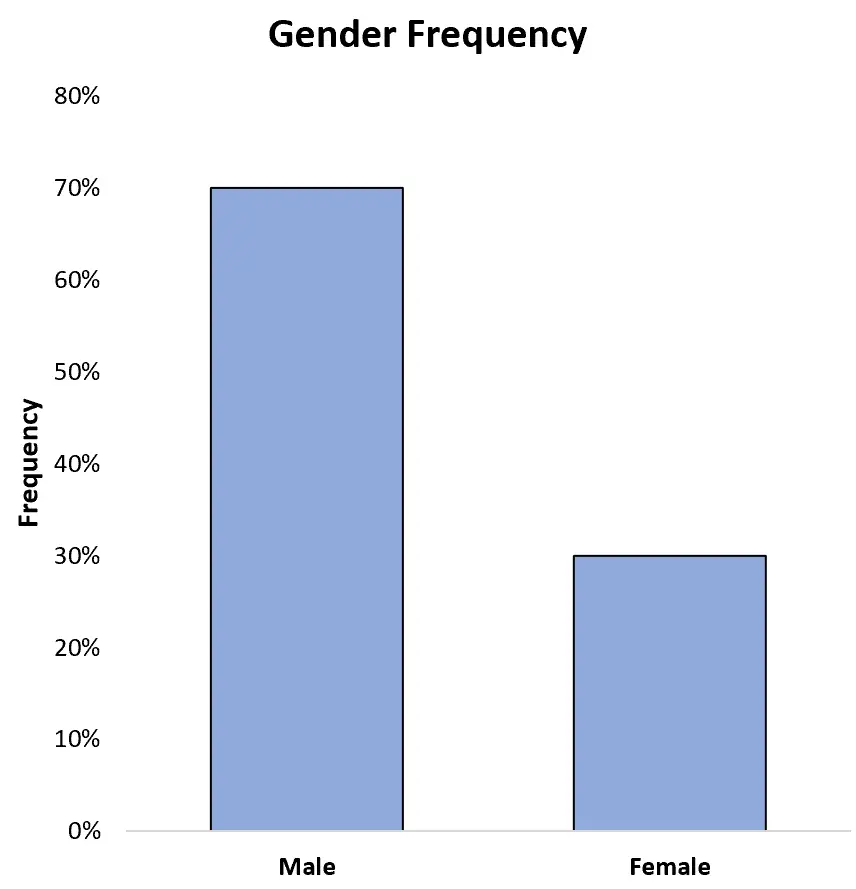
Это позволяет нам легко увидеть, что 70% от общего числа спортсменов в наборе данных — мужчины, а 30% — женщины.

Как анализировать дихотомические переменные

Существует несколько способов анализа дихотомических переменных. К двум наиболее распространенным методам относятся:

1. Однопропорциональный z-критерий

Z-тест для одной пропорции определяет, равна ли наблюдаемая пропорция теоретической пропорции.

Например, мы могли бы использовать этот тест, чтобы определить, равна ли истинная доля спортсменов-мужчин в данной популяции 50%.

2. Точечно-бисериальная корреляция

Точечно-бисериальная корреляция используется для измерения взаимосвязи между дихотомической переменной и непрерывной переменной.

Этот тип корреляции принимает значение от -1 до 1, где:

• -1 указывает на совершенно отрицательную корреляцию между двумя переменными.
• 0 указывает на отсутствие корреляции между двумя переменными.
• 1 указывает на совершенно положительную корреляцию между двумя переменными.

Например, мы могли бы рассчитать корреляцию между полом и средним количеством очков за игру, чтобы понять, насколько тесно связаны эти две переменные.