Доверительный интервал для разницы средних
В этой статье объясняется, что такое доверительный интервал для разницы средних в статистике и для чего он используется. Итак, вы узнаете, как рассчитать доверительный интервал для разницы двух средних и пошагово решить упражнение.
Каков доверительный интервал для разницы средних?
Доверительный интервал для разницы средних значений — это интервал, который обеспечивает максимальное значение и минимальное значение, между которыми с определенным уровнем достоверности лежит значение разницы средних двух популяций.
Например, если доверительный интервал для разницы средних значений двух совокупностей с уровнем достоверности 95% равен (3,5), это означает, что разница между средними значениями двух совокупностей будет между 3 и 5 с вероятностью 95. %.
Поэтому в статистике доверительный интервал разницы средних значений используется для оценки двух значений, между которыми находится разница между двумя средними значениями совокупности. Таким образом, используя данные двух выборок, можно аппроксимировать разницу между средними значениями генеральной совокупности.
Формула доверительного интервала для разницы средних значений
Формула доверительного интервала для разницы средних зависит от того, известны или нет дисперсии совокупности, а если нет, то можно ли считать дисперсии совокупности равными. . Затем мы увидим, как рассчитывается доверительный интервал для разницы средних значений в каждом случае.
известные отклонения
Формула для расчета доверительного интервала для разницы средних значений, когда дисперсии двух совокупностей известны с уровнем достоверности 1-α, выглядит следующим образом:
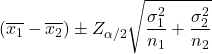
Золото:
-

является средним значением выборки i.
-

— стандартное отклонение генеральной совокупности i.
-

— значение стандартного нормального распределения с вероятностью α/2.
-

размер выборки i.
Этот случай является наименее распространенным, поскольку значение дисперсии генеральной совокупности обычно неизвестно.
неизвестные и равные дисперсии
Когда дисперсии двух совокупностей неизвестны, но могут быть оценены как равные, формула для расчета доверительного интервала для разницы средних значений с уровнем достоверности 1-α выглядит следующим образом:
![]()
Золото:
-

является средним значением выборки i.
-

— объединенное стандартное отклонение.
-

— значение t-распределения Стьюдента n 1 + n 2 -2 степеней свободы с вероятностью α/2.
-

размер выборки i.
Поскольку в этом случае предполагается, что дисперсии генеральной совокупности эквивалентны, для расчета доверительного интервала используется комбинированное стандартное отклонение, которое рассчитывается по следующей формуле:

Золото
![]()
— стандартное отклонение выборки i.
Неизвестные и разные вариации
Когда дисперсии двух совокупностей неизвестны и не могут считаться равными, формула для расчета доверительного интервала для разницы средних значений с уровнем достоверности 1-α выглядит следующим образом:
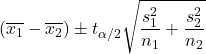
Золото:
-

является средним значением выборки i.
-
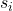
— стандартное отклонение выборки i.
-

— значение распределения Стьюдента с вероятностью α/2.
-

размер выборки i.
В этом случае степени свободы t-распределения Стьюдента рассчитываются по следующей формуле:

Золото
![]()
— стандартное отклонение выборки i.
Конкретный пример доверительного интервала для разницы средних значений
После ознакомления с определением доверительного интервала для разницы средних значений и того, что представляют собой различные формулы, мы теперь рассмотрим конкретный пример, чтобы закончить понимание того, как рассчитывается доверительный интервал для разницы двух средних значений.
- Мы хотим изучить влияние табака на вес детей при рождении. Для этого сравниваются две выборки: первая выборка состоит из детей, матери которых не курили, и вторая выборка из детей, матери которых курили (параметры выборки указаны ниже). Рассчитайте доверительный интервал для разницы средних значений с уровнем достоверности 95%.
- Некурящие матери:
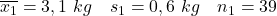
- Курящие матери:
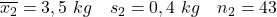
- Некурящие матери:
В этом случае мы не знаем значения популяционных дисперсий, однако можем предположить, что популяционные дисперсии эквивалентны, поскольку мы имеем дело с двумя популяциями с очень похожими характеристиками. Следовательно, формула доверительного интервала для разницы средних, которую нам следует использовать, выглядит следующим образом:
![]()
Таким образом, мы вычисляем комбинированное стандартное отклонение из стандартных отклонений двух выборок:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
Аналогично мы должны найти значение t-распределения Стьюдента 80 степеней свободы с вероятностью 2,5% в таблице распределения вероятностей t-распределения Стьюдента :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Наконец, подставляем данные в формулу доверительного интервала для разницы средних и выполняем расчеты:
![]()
![]()
![]()
Таким образом, доверительный интервал для разницы средних значений задачи выглядит следующим образом:
![]()