Меры центральной тенденции: определение и примеры
Мера центральной тенденции — это одно значение, которое представляет собой центральную точку набора данных. Это значение также можно назвать «центральным расположением» набора данных.
В статистике есть три распространенных показателя центральной тенденции:
- Среднее
- Медиана
- Мода
Каждая из этих мер находит центральное расположение набора данных, используя разные методы. В зависимости от типа данных, которые вы анализируете, возможно, лучше использовать один из этих трех показателей, а не два других.
В этой статье мы рассмотрим, как рассчитать каждую из трех мер центральной тенденции, а также как определить, какую меру лучше всего использовать на основе ваших данных.
Почему полезны измерения центральной тенденции?
Прежде чем мы рассмотрим, как рассчитать среднее значение, медиану и моду, полезно понять , почему эти измерения вообще полезны.
Рассмотрим следующий сценарий:
Молодая пара пытается решить, где купить свой первый дом в новом городе, и максимум, что они могут потратить, это 150 000 долларов. В некоторых районах города есть дорогие дома, в некоторых — дешевые, а в некоторых — дома средней ценовой категории. Они хотят легко сузить поиск до конкретных районов, соответствующих их бюджету.
Если бы пара просто посмотрела на цены домов на одну семью в каждом районе, у них могли бы возникнуть трудности с определением того, какой район лучше всего соответствует их бюджету, потому что они могли бы увидеть что-то вроде этого:
Цены на дома в районе А : 140 000 долларов, 190 000 долларов, 265 000 долларов, 115 000 долларов, 270 000 долларов, 240 000 долларов, 250 000 долларов, 180 000 долларов, 160 000 долларов, 200 000 долларов, 240 000 долларов, 280 000 долларов,…
Цены на дома в районе B : 140 000 долларов, 290 000 долларов, 155 000 долларов, 165 000 долларов, 280 000 долларов, 220 000 долларов, 155 000 долларов, 185 000 долларов, 160 000 долларов, 200 000 долларов, 190 000 долларов, 140 000 долларов, 145,0 долларов США. 0 0,…
Цены на дом в районе C : 140 000, 130 000, 165 000, 115 000, 170 000, 100 000, 150 000, 180 000, 190 000, 120 000, 110 000, 130 000, 120,0 $. 0 0,…
Однако если бы они знали среднюю цену (например, показатель центральной тенденции) домов в каждом районе, то они могли бы уточнить свой поиск гораздо быстрее, поскольку им было бы легче определить, в каком районе цены на жилье соответствуют их бюджету:
Средняя цена дома в районе А: 220 000 долларов.
Средняя цена дома в районе Б : 190 000 долларов.
Средняя цена дома в районе C : 140 000 долларов.
Зная среднюю цену дома в каждом районе, они могут быстро увидеть, что в районе C , вероятно, будет больше всего домов, доступных в рамках их бюджета.
В этом преимущество использования меры центральной тенденции: она помогает вам понять центральное значение набора данных, которое имеет тенденцию описывать, где обычно лежат значения данных. В данном конкретном примере это помогает молодой паре понять типичную цену дома в каждом районе.
Вывод: Измерение центральной тенденции полезно, поскольку оно дает нам единственное значение, которое описывает «центр» набора данных. Это помогает нам понять набор данных гораздо быстрее, чем просто просматривать все отдельные значения в наборе данных.
Иметь в виду
Наиболее часто используемой мерой центральной тенденции является среднее значение . Чтобы вычислить среднее значение набора данных, просто сложите все отдельные значения и разделите на общее количество значений.
Среднее = (сумма всех значений) / (общее количество значений)
Например, предположим, что у нас есть следующий набор данных, который показывает количество хоумранов, совершенных 10 бейсболистами одной команды в течение сезона:
| Игрок | №1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоумраны | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Среднее количество хоумранов на одного игрока можно рассчитать следующим образом:
Среднее = (8+15+22+21+12+9+11+27+14+13)/10 = 15,2 круга .
медиана
Медиана — это среднее значение набора данных. Медиану можно найти, упорядочив все отдельные значения в наборе данных от наименьшего к наибольшему и найдя медианное значение. Если имеется нечетное количество значений, медианой является среднее значение. Если имеется четное количество значений, медиана представляет собой среднее значение двух средних значений.
Например, чтобы найти среднее количество хоумранов, совершенных 10 бейсболистами из предыдущего примера, мы можем ранжировать игроков в порядке убывания количества хоумранов:
| Игрок | №1 | #6 | #7 | #5 | #десять | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоумраны | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Поскольку у нас четное количество значений, медиана — это просто среднее двух средних значений: 13,5 .
Вместо этого предположим, что у нас было девять игроков:
| Игрок | №1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Хоумраны | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
В этом случае, поскольку у нас нечетное количество значений, медиана — это просто среднее значение: 14 .
Мода
Режим — это значение, которое чаще всего появляется в наборе данных. Набор данных может не иметь режимов (если значения не повторяются), иметь один режим или несколько режимов.
Например, следующий набор данных не имеет режима:
| Игрок | №1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоумраны | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Следующий набор данных имеет режим: 15 . Это значение, которое встречается чаще всего.
| Игрок | №1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоумраны | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
Следующий набор данных имеет три режима: 8, 15, 19 . Это значения, которые встречаются чаще всего.
| Игрок | №1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоумраны | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Мода может быть особенно полезной мерой центральной тенденции при работе с категориальными данными, поскольку она сообщает нам, какая категория появляется чаще всего. Например, рассмотрим следующую гистограмму, на которой показаны результаты опроса о любимом цвете людей:
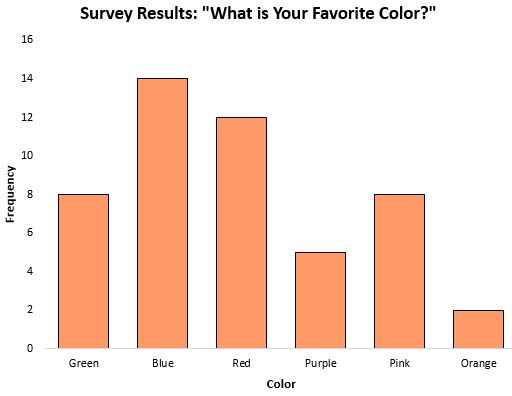
Режим или ответ, который возникал чаще всего, был синим.
В сценариях, где данные являются категориальными (как показано выше), невозможно даже вычислить медиану или среднее значение, поэтому мода является единственной мерой центральной тенденции, которую мы можем использовать.
Этот режим также можно использовать для числовых данных, как мы видели в приведенном выше примере с бейсболистами. Однако режим, как правило, менее полезен для ответа на вопрос «Каково типичное значение для этого набора данных?» »
Например, предположим, что мы хотим узнать типичное количество хоумранов, совершенных бейсболистом этой команды:
| Игрок | №1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоумраны | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Режим для этого набора данных — 8, 15 и 19, поскольку это наиболее часто встречающиеся значения. Однако они не очень помогают понять типичное количество хоумранов, совершаемых игроком команды. Лучшим показателем центральной тенденции в этом случае будет медиана (15) или среднее значение (также 15).
Мода также является плохой мерой центральной тенденции, если ее число далеко от остальных значений. Например, режим следующего набора данных равен 30, но на самом деле он не отражает «типичное» количество хоумранов на одного игрока в команде:
| Игрок | №1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоумраны | 5 | 6 | 7 | десять | 11 | 12 | 13 | 15 | 30 | 30 |
Опять же, среднее значение или медиана лучше описывают центральное расположение этого набора данных.
Когда использовать среднее значение, медиану и моду
Мы видели, что среднее значение, медиана и мода измеряют центральное местоположение или «типичное значение» набора данных разными способами:
Среднее: находит среднее значение в наборе данных.
Медиана: находит медианное значение в наборе данных.
Режим: находит наиболее часто встречающееся значение в наборе данных.
Вот сценарии, в которых одни меры центральной тенденции лучше использовать, чем другие:
Когда использовать среднее значение
Лучше всего использовать среднее значение, когда распределение данных достаточно симметрично и нет выбросов.
Например, предположим, что у нас есть следующее распределение, которое показывает зарплаты людей в определенном городе:

Поскольку это распределение довольно симметрично (т. е. если разделить его пополам, каждая половина будет выглядеть примерно одинаковой) и в нем нет выбросов (т. е. (скажем, нет чрезвычайно высоких зарплат), среднее значение хорошо опишет этот набор данных.
В среднем получается 63 000 долларов, что примерно в центре распределения:

Когда использовать медиану
Медиану лучше всего использовать, когда распределение данных искажено или имеются выбросы.
Смещенные данные:
Когда распределение искажено, медиане все равно удается уловить центральное положение. Например, рассмотрим следующее распределение зарплат физических лиц в определенном городе:

Медианное значение лучше отражает «типичную» зарплату человека, чем среднее значение. Это связано с тем, что большие значения в хвосте распределения имеют тенденцию смещать среднее значение от центра к длинному хвосту.
В этом конкретном примере среднее значение говорит нам, что типичный человек зарабатывает около 47 000 долларов в год в этом городе, в то время как медиана говорит нам, что типичный человек зарабатывает только около 32 000 долларов в год, что гораздо более репрезентативно для типичного человека.
Выбросы:
Медиана также помогает лучше определить центральное расположение распределения, когда в данных есть выбросы. Например, рассмотрим следующий график, показывающий площадь домов на определенной улице:

На среднее значение сильно влияют несколько чрезвычайно больших домов, а на медиану — нет. Таким образом, медианное значение лучше отражает «типичную» площадь дома на этой улице, чем среднее значение.
Когда использовать режим
Этот режим лучше всего использовать, когда вы работаете с категориальными данными и хотите знать, какая категория появляется чаще всего. Вот некоторые примеры:
- Вы проводите опрос о любимых цветах людей и хотите узнать, какой цвет чаще всего встречается в ответах.
- Вы проводите опрос предпочтений людей среди трех вариантов дизайна веб-сайта и хотите узнать, какой дизайн люди предпочитают больше всего.
Как упоминалось ранее, если вы работаете с категориальными данными, невозможно даже вычислить медиану или среднее значение, в результате чего мода остается единственной мерой центральной тенденции.
В общем, если вы работаете с числовыми данными, такими как квадратные метры домов, количество хоумранов на игрока, зарплата на человека и т. д., обычно лучше использовать медианное или среднее значение для описания значения «типичное» в набор данных.
Примечание. Важно отметить, что если набор данных имеет совершенно нормальное распределение, то среднее значение, медиана и мода имеют одинаковое значение.