Как читать коробчатую диаграмму с выбросами (с примером)
Ящичковая диаграмма — это тип графика, на котором отображается пятизначная сводка набора данных, которая включает в себя:
- Минимальное значение
- Первый квартиль (25-й процентиль)
- Медианное значение
- Третий квартиль (75-й процентиль)
- Максимальное значение
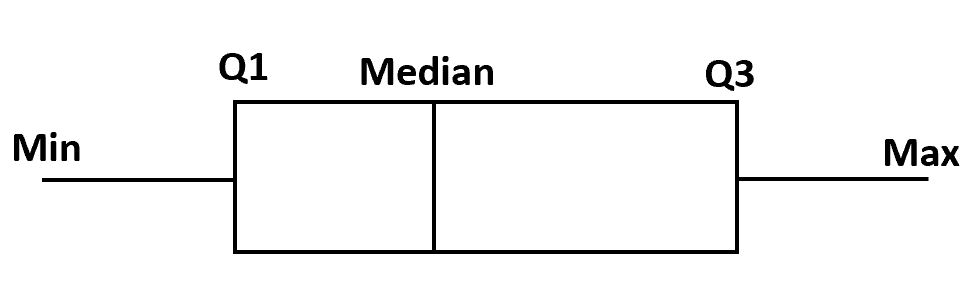
Чтобы построить коробчатую диаграмму, мы сначала рисуем прямоугольник от первого до третьего квартиля.
Далее проводим вертикальную линию посередине.
Наконец, рисуем «усы» квартилей до минимального и максимального значения.
В большинстве статистических программ наблюдение определяется как выброс, если оно соответствует одному из следующих двух требований:
- Наблюдение в 1,5 раза превышает межквартильный размах ниже первого квартиля (Q1).
- Наблюдение в 1,5 раза превышает межквартильный размах выше третьего квартиля (Q3).
Если в наборе данных существует выброс, он обычно помечается маленькой точкой за пределами диапазона «усов» на прямоугольной диаграмме:

Когда это происходит, «минимальному» и «максимальному» значениям на диаграмме просто присваиваются значения Q1 – 1,5*IQR и Q3 + 1,5*IQR соответственно.
В следующем примере показано, как интерпретировать коробчатые диаграммы с выбросами и без них.
Пример. Интерпретация коробчатой диаграммы с выбросами
Предположим, мы создаем следующие две коробчатые диаграммы, чтобы визуализировать распределение очков, набранных баскетболистами из двух разных команд:
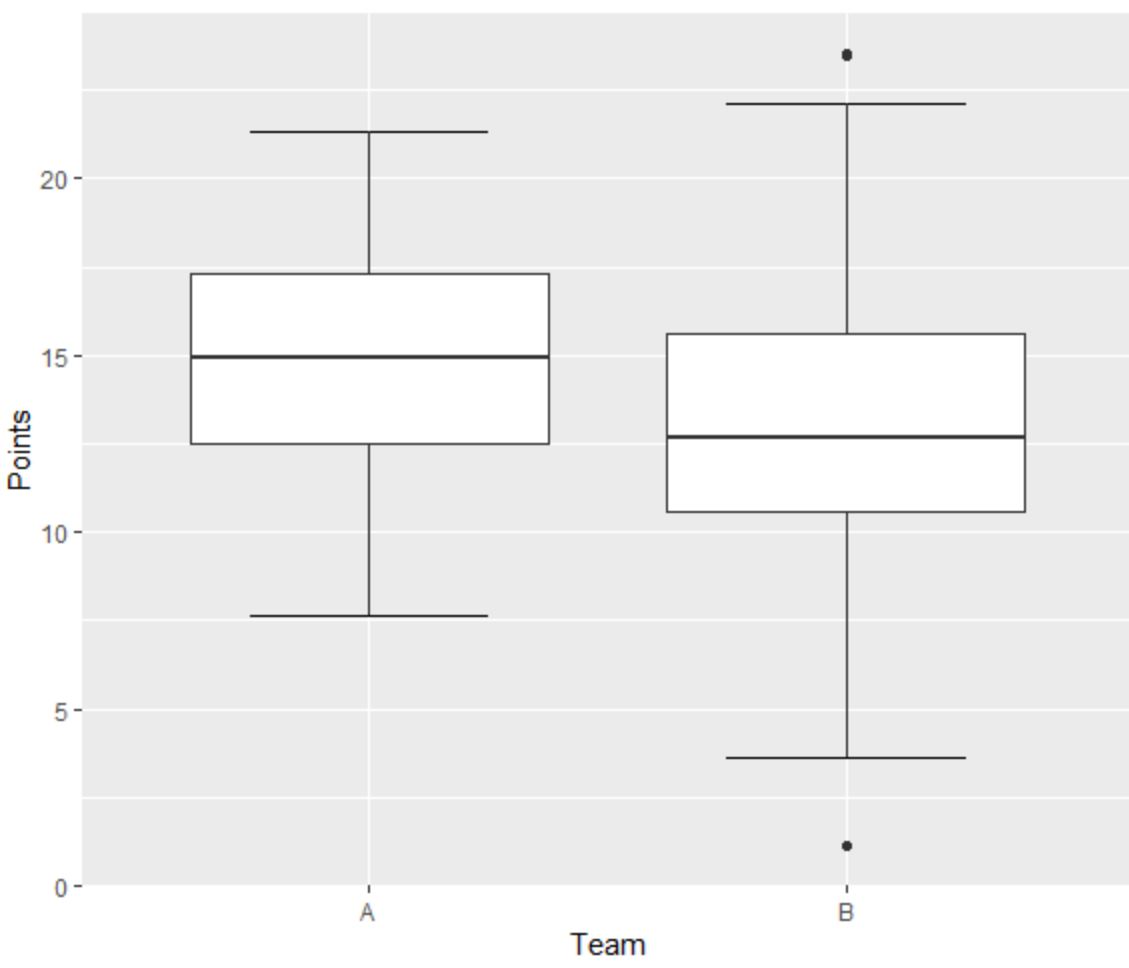
Левая диаграмма для команды А не имеет выбросов, поскольку нет маленьких точек, расположенных за пределами минимального или максимального уса.
Однако правый коробчатый график для команды B имеет один выброс выше «максимального» значения и один выброс ниже «минимального» значения.
Вот текущая пятизначная сводка распределения переменной «Очки» для Команды Б:
- Минимальное значение: 1,1
- Первый квартиль: 10,5
- Медиана: 12,7
- Третий квартиль: 15,6
- Максимальное значение: 23,5
Вот как можно рассчитать пределы потенциальных выбросов:
Межквартильная шкала : Третий квартиль – Первый квартиль = 15,6 – 10,5 = 5,1.
Нижний предел : Q1 – 1,5*IQR = 10,5 – 1,5*5,1 = 2,85
Верхний предел : Q3 + 1,5*IQR = 15,6 + 1,5*5,1 = 23,25.
Усы для минимального и максимального значений на диаграмме расположены на 2,85 и 23,25 .
Таким образом, наблюдения со значениями 1,1 и 23,5 квалифицируются как выбросы на коробчатой диаграмме, поскольку они выходят за пределы нижней и верхней границ.
Бонус : вот точный код, который мы использовали для создания этих двух коробчатых диаграмм на языке программирования R:
library (ggplot2) #make this example reproducible set. seeds (2) #create data frame df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), Points = c(rnorm(200, mean = 15, sd = 3), rnorm(200, mean = 12, sd = 4))) #create box plots ggplot(df, aes(x = Team, y = Points)) + stat_boxplot(geom = " errorbar ", width = 0.5) + geom_boxplot() #calculate summary statistics for each team tapply(df$Points, df$Team, summary)
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о коробчатых диаграммах:
Как сравнивать коробчатые диаграммы
Как определить асимметрию в коробчатых диаграммах
Как найти межквартильный размах коробчатой диаграммы