Как читать таблицу биномиального распределения

Таблица биномиального распределения   представляет собой таблицу, показывающую вероятности, связанные с биномиальным распределением . Чтобы использовать таблицу биномиального распределения, вам нужны всего три значения:

• n: количество попыток
• r: количество «успехов» за n попыток.
• p: вероятность успеха данного испытания.

Используя эти три числа, вы можете использовать таблицу биномиального распределения, чтобы найти вероятность получения ровно r успехов в ходе n испытаний, когда вероятность успеха в каждом испытании равна p .

Следующие примеры иллюстрируют, как читать таблицу биномиального распределения.

Пример 1

Вопрос: Джессика выполняет 60% штрафных бросков. Если она выполнит 6 штрафных бросков, какова вероятность того, что она выполнит ровно 4?

Чтобы ответить на этот вопрос, мы можем найти в таблице биномиального распределения значение, соответствующее n = 6, r = 4 и p = 0,60:

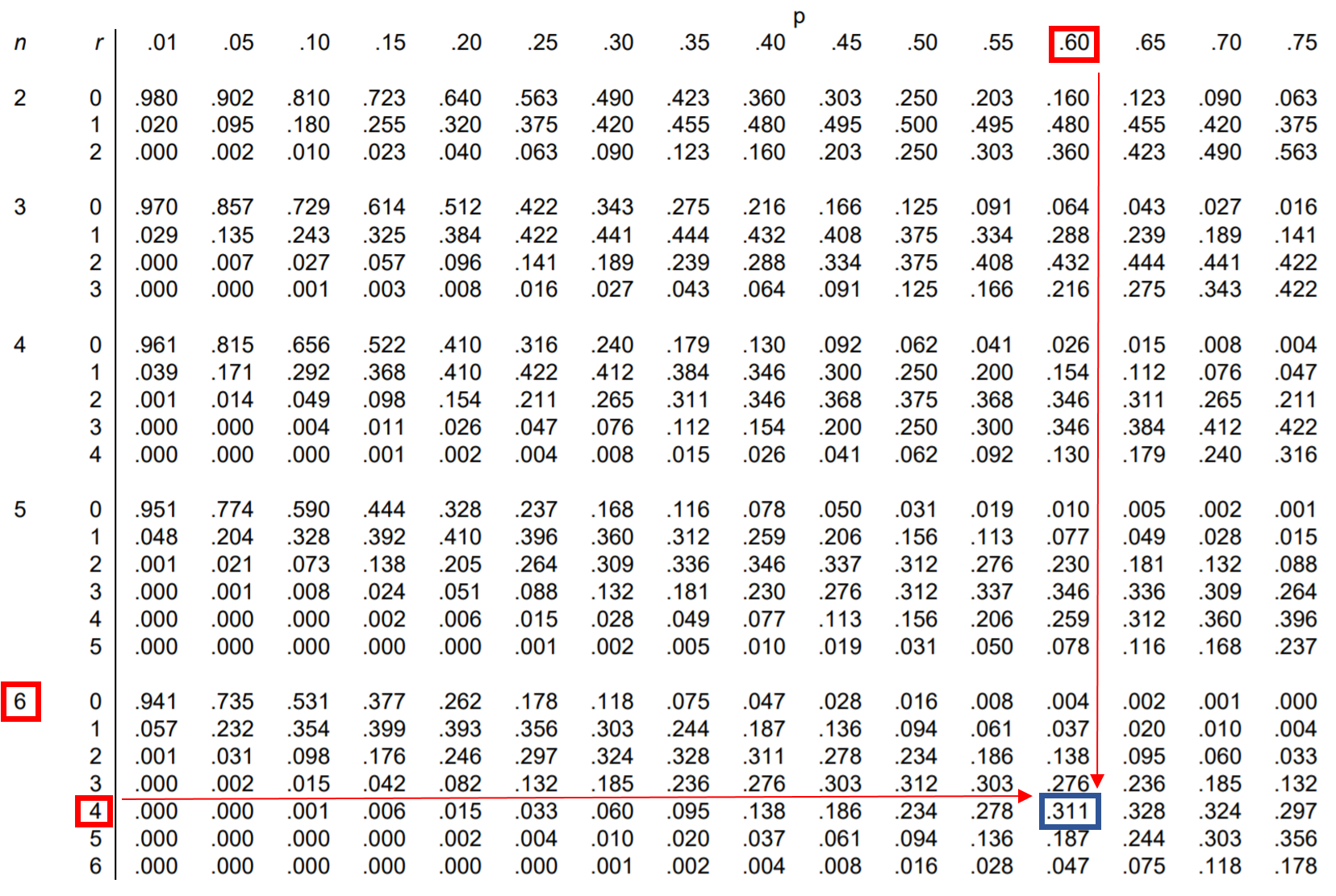
Вероятность того, что Джессика выполнит ровно 4 штрафных броска из 6, равна 0,311 .

Пример 2

Вопрос: Джессика выполняет 60% штрафных бросков. Если она выполнит 6 штрафных бросков, какова вероятность того, что она выполнит меньше 4?

Чтобы найти эту вероятность, вам фактически нужно сложить следующие вероятности:

P(даёт меньше 4) = P(даёт 0) + P(даёт 1) + P(даёт 2) + P(даёт 3)

Итак, мы можем найти каждую из этих четырех вероятностей в таблице биномиального распределения и сложить их вместе:

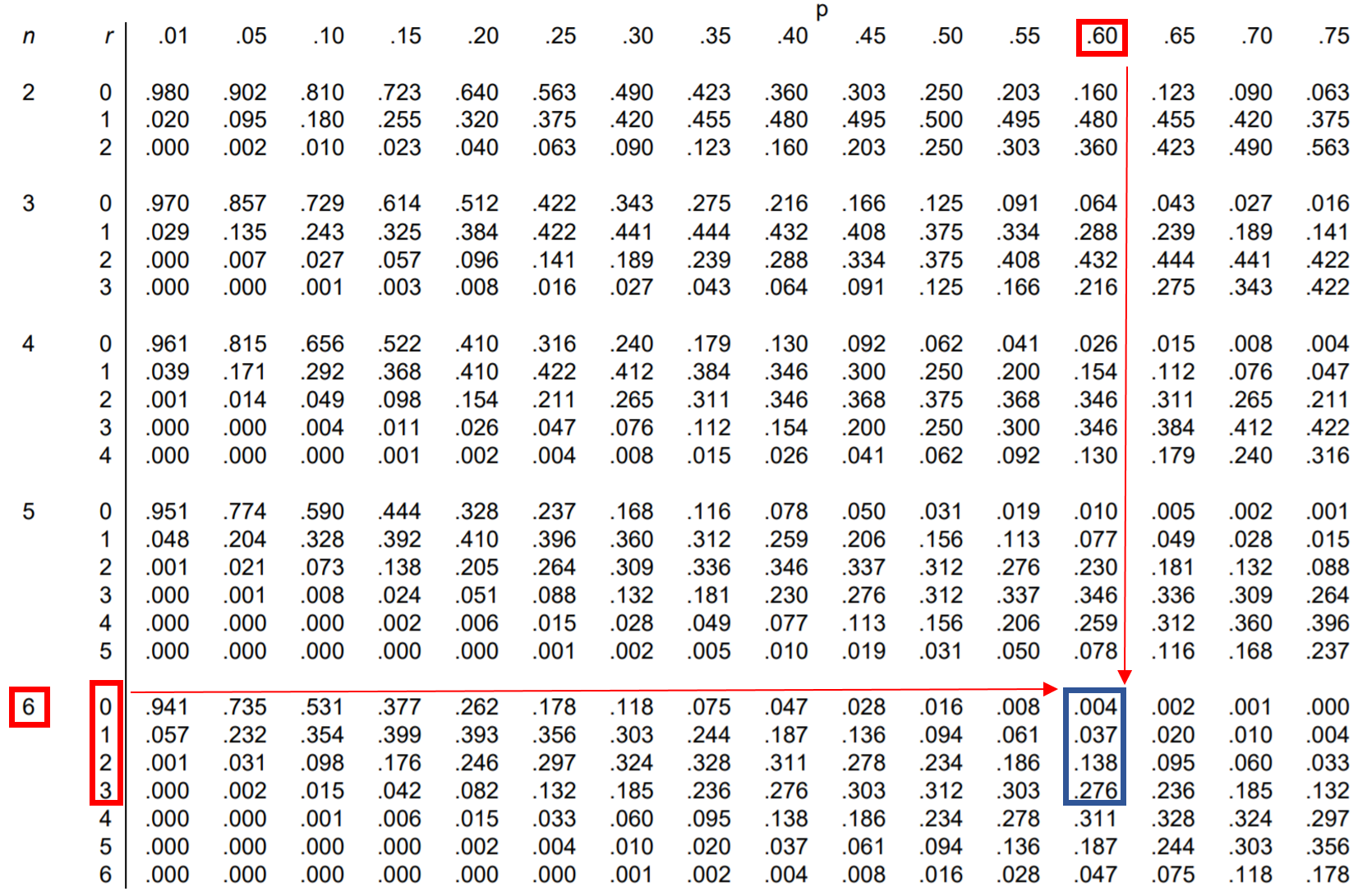
Согласно таблице P(меньше 4) = 0,004 + 0,037 + 0,138 + 0,276 = 0,455 .

Вероятность того, что Джессика выполнит менее 4 штрафных бросков, равна 0,455 .

Пример 3

Вопрос: Джессика выполняет 60% штрафных бросков. Если она выполнит 6 штрафных бросков, какова вероятность того, что она выполнит 4 или более?

Чтобы найти эту вероятность, необходимо сложить следующие вероятности:

P(делает 4 или больше) = P(делает 4) + P(делает 5) + P(делает 6)

Итак, мы можем найти каждую из этих трех вероятностей в таблице биномиального распределения и сложить их вместе:

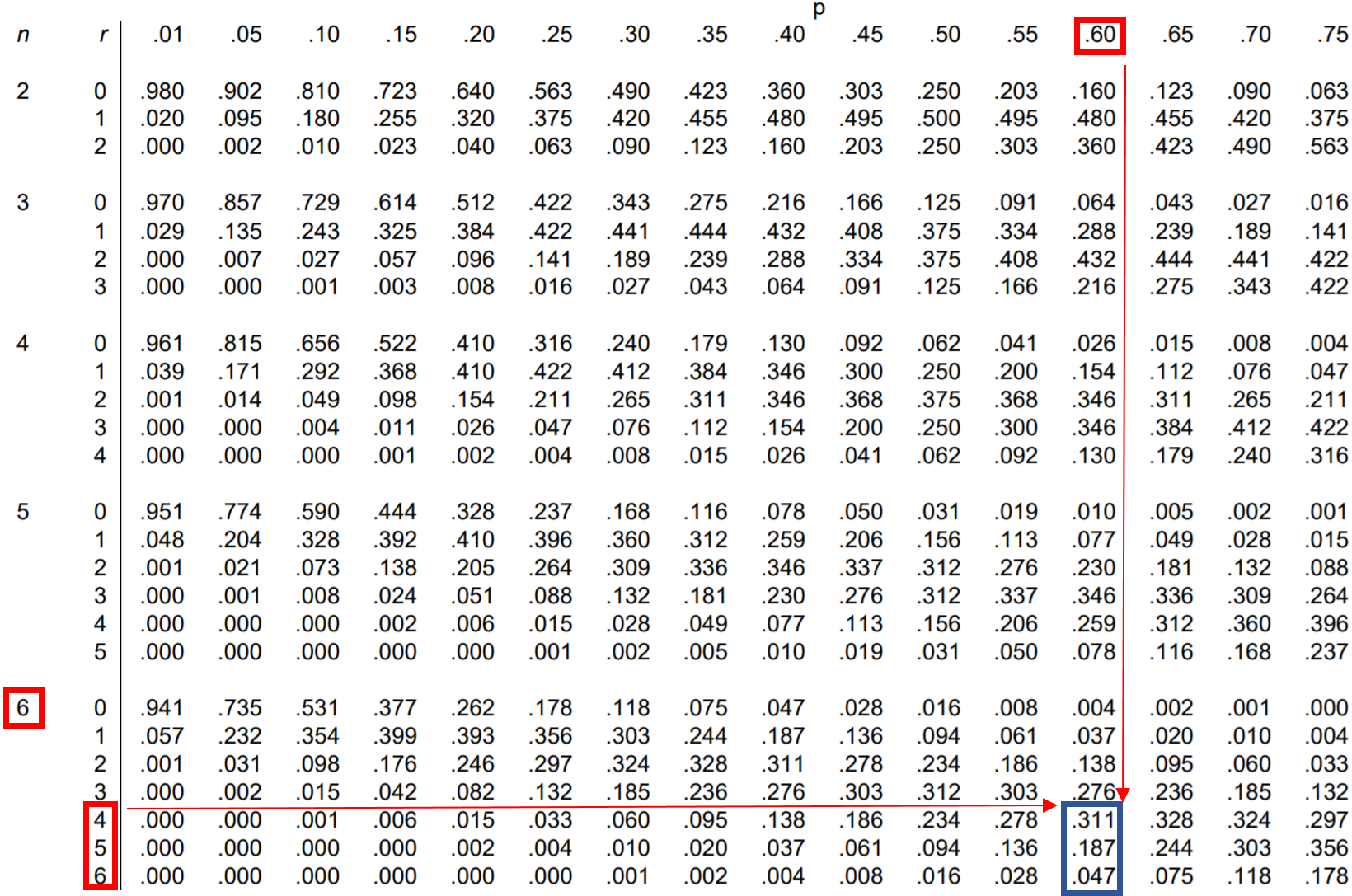
Согласно таблице P (составляет 4 или более) = 0,311 + 0,187 + 0,047 = 0,545 .

Вероятность того, что Джессика выполнит 4 или более штрафных броска, равна 0,545 .