Квазивариантность

В этой статье объясняется, что такое квазивариантность в статистике. Таким образом, вы узнаете, как рассчитать квазивариацию, решить упражнение и в чем разница между квазивариантностью и дисперсией. Кроме того, вы можете рассчитать квазивариацию любого набора данных с помощью онлайн-калькулятора.

Что такое квазивариантность?

В статистике квазивариантность — это мера дисперсии, которая указывает на изменчивость выборки. Точнее, квазивариантность равна сумме квадратов отклонений, деленной на общее количество наблюдений минус один.

Символ квазивариантности:

или

. иногда Хотя этот символ также используется

для представления квазивариантности.

Квазивариация используется для определения дисперсии выборки, избегая при этом систематической ошибки, поэтому ее часто называют несмещенной дисперсией. Таким образом, квазивариантность является хорошей оценкой генеральной дисперсии. Фактически, при расчете выборочной дисперсии вместо формулы дисперсии часто используется формула квазидисперсии. Ниже мы подробно остановимся на разнице между этими двумя статистическими показателями.

Формула квазивариации

Чтобы вычислить квазивариацию, нужно найти сумму квадратов разностей между значениями и средним значением набора данных, а затем разделить ее на общее количество данных минус один.

Итак, формула для расчета квазивариации выглядит следующим образом:

Золото:

• 

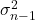
  является квазивариантностью.

• 

  значение данных

  

  .

• 

  общее количество данных.

• 

  является средним значением набора данных.

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать квазивариацию любого набора данных.

Вам может быть интересно, почему оно делится на n-1, а не на n? Ну, речь идет об устранении смещения, таким образом мы получаем несмещенную оценку. Именно поэтому квазивариантность является хорошей оценкой генеральной дисперсии.

Пример расчета квазивариации

Теперь, когда мы знаем определение квазивариантности, мы решим простой пример, чтобы вы могли увидеть, как рассчитывается квазивариантность ряда данных.

• От транснациональной компании мы знаем экономический результат, который она добилась за последние пять лет, в большинстве случаев она получила прибыль, но за один год она принесла значительные убытки: 11,5, 2, -9, 7 миллионов евро. Вычислите квазивариантность этого набора данных.

Первое, что нам нужно сделать, чтобы получить квазивариантность набора данных, — это вычислить его среднее арифметическое:

И как только мы узнаем среднее значение данных, мы применим формулу квазивариации:

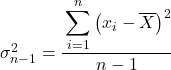
Итак, подставляем данные, предусмотренные инструкцией по упражнению, в формулу:

Наконец, достаточно решить операции по вычислению квазивариации:

Обратите внимание, что единицы квазивариации — это те же единицы, что и единицы статистических данных, но возведенные в квадрат, поэтому квазивариация этого набора данных равна 57,2 миллиона ² .

Калькулятор квазивариации

Введите набор статистических данных в следующий калькулятор, чтобы рассчитать его квазивариантность. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Дисперсия и квазивариантность

Наконец, мы увидим разницу между квазивариантностью и дисперсией, поскольку, несмотря на схожесть названия, они также рассчитываются очень похоже.

Разность между квазивариацией и дисперсией является знаменателем формулы. Чтобы вычислить квазивариантность, необходимо разделить на n-1, однако дисперсия рассчитывается путем деления на n.

Таким образом, квазивариантность и дисперсия математически связаны, поскольку квазивариантность эквивалентна дисперсии, умноженной на n (общее количество точек данных) и разделенной на n-1.

Следовательно, для одного и того же набора данных значение квазивариации всегда будет больше значения дисперсии.