Квартили

В этой статье мы объясним, что такое квартили. Вы найдете определение каждого квартиля, способы его расчета и несколько конкретных примеров. Мы также покажем вам, как рассчитать квартили для сгруппированных данных. Кроме того, вы сможете рассчитать квартили любого набора данных с помощью онлайн-калькулятора.

Что такое квартили?

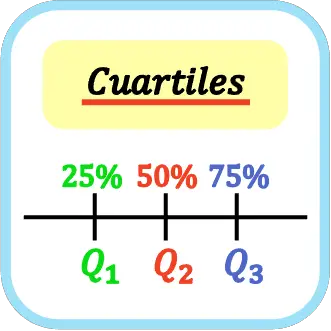
В статистике квартили — это три значения, которые делят набор упорядоченных данных на четыре равные части. Таким образом, первый, второй и третий квартили представляют соответственно 25%, 50% и 75% всех статистических данных.

Квартили обозначаются заглавной буквой Q и индексом квартиля, поэтому первый квартиль — это Q ₁ , второй квартиль — Q ₂ и третий квартиль — Q ₃ .

👉 Вы можете использовать калькулятор ниже для расчета квартилей любого набора данных.

Следует отметить, что квартили являются мерой нецентрального положения так же, как квинтили, децили и процентили. Вы можете проверить, что представляет собой каждый из этих типов квантилей, на этой веб-странице.

первый квартиль

Первый квартиль , также называемый квартилем 1, представляет собой значение, превышающее 25 % статистических данных в выборке. Другими словами, первый квартиль представляет более 25% наблюдаемых данных.

Первый квартиль обозначается символом Q ₁ и используется для обозначения наименьших значений данных в выборке.

второй квартиль

Второй квартиль , также называемый квартилем 2, представляет собой значение, превышающее 50 % статистических данных в выборке. Таким образом, второй квартиль разделяет набор данных на две половины и совпадает с медианой и пятым децилем.

Символ второго квартиля — _Q2 .

третий квартиль

Третий квартиль , также называемый 3-м квартилем, — это значение, которое превышает 75% статистических данных в выборке. Другими словами, третий квартиль представляет более 75% собранных данных.

Третий квартиль обозначается символом Q ₃ и представляет собой самые большие значения в выборке.

Как посчитать квартили

Чтобы вычислить положение квартилей набора статистических данных, необходимо умножить количество квартилей на сумму общего количества данных плюс один и разделить результат на четыре.

Таким образом, формула для квартилей выглядит следующим образом:

Обратите внимание: эта формула сообщает нам положение квартиля, а не его значение. Квартилем будут данные, расположенные в позиции, полученной по формуле.

Однако иногда результат этой формулы даст нам десятичное число. Поэтому мы должны различать два случая в зависимости от того, является ли результат десятичным числом или нет:

• Если результатом формулы является число без десятичной части , квартилем являются данные, находящиеся в позиции, указанной в формуле выше.
• Если результатом формулы является число с десятичной частью , значение квартиля рассчитывается по следующей формуле:

Где x _i и x _i+1 – номера позиций, между которыми находится число, полученное по первой формуле, а d – десятичная часть числа, полученного по первой формуле.

Возможно, вычисление квартилей для вас очень сложное, потому что нужно учитывать множество вещей. Но с помощью двух примеров в следующем разделе вы увидите, насколько это на самом деле довольно просто.

Примечание . В научном сообществе нет единого мнения о том, как вычислять квартили, поэтому вы можете найти книгу по статистике, объясняющую это немного по-другому.

Примеры расчета квартилей

Чтобы полностью понять, как рассчитываются квартили, ниже вы найдете два решенных упражнения. В первом случае квартилями являются целые числа, а во втором — десятичные числа, поэтому вы можете увидеть, какие два случая вы можете найти.

Пример 1

• Рассчитайте три квартиля следующего набора данных:

Как мы видели выше, формула определения квартилей такова:

В этом случае n общее количество наблюдений равно 15, поэтому мы должны заменить n на 15 и k на 1, чтобы найти первый квартиль:

Следовательно, первый квартиль — это число на четвертой позиции упорядоченного списка значений, которое в данном случае равно 39.

Аналогично вычисляем второй квартиль, заменив коэффициент k на 2:

Таким образом, квартиль 2 — это восьмое число в отсортированном списке, что соответствует значению 48.

Наконец, мы применяем формулу в последний раз с k = 3 для расчета третьего квартиля:

Квартиль 3 соответствует данным на двенадцатой позиции, т.е. 60.

Пример 2

• Найдите три квартиля следующего ряда данных:

Во втором примере у нас 24 наблюдения, поэтому числа, полученные по формуле квартиля, будут десятичными.

Сначала вычислим положение первого квартиля, подставив k вместо 1 в общую формулу:

Но у нас получилось десятичное число 6,25, поэтому первый квартиль лежит между шестым и седьмым данными, которые равны 22 и 25 соответственно. Следовательно, для расчета точного квартиля нам необходимо применить следующую формулу:

В данном случае x _i равно 22, x _i+1 25 и d представляет собой десятичную часть полученного числа, т.е. 0,25. Еще:

Теперь проделаем ту же процедуру, чтобы найти второй квартиль:

Снова получаем десятичное число по формуле, в данном случае это 12,5. Поэтому мы должны использовать ту же формулу с двенадцатым и тринадцатым числами в таблице данных, что соответствует 49 и 50:

Наконец, мы повторяем тот же процесс, чтобы получить третий квартиль:

А вот число 18,75 находится между числами 18 и 19, поэтому третий квартиль будет между значениями этих позиций (71 и 73). Точнее, это будет значение, которое мы получим из следующего выражения:

калькулятор квартилей

Подключите набор статистических данных к калькулятору ниже, чтобы рассчитать квартили. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Квартили в сгруппированных данных

Чтобы вычислить квартиль, когда данные сгруппированы в интервалы, нам сначала нужно найти интервал или интервал, в который попадает квартиль, используя следующую формулу:

Таким образом, квартиль будет находиться в интервале, абсолютная совокупная частота которого сразу больше числа, полученного с помощью предыдущего выражения.

И как только мы узнаем интервал, к которому принадлежит квартиль, мы должны применить следующую формулу, чтобы найти точное значение квартиля:

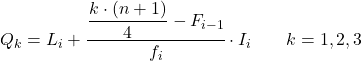
Золото:

• _Li — нижняя граница интервала, в котором лежит квартиль.
• n — общее количество наблюдений.
• F _i-1 представляет собой совокупную абсолютную частоту предыдущего интервала.
• f _i — абсолютная частота интервала, в котором лежит квартиль.
• I _i – ширина квартильного интервала.

В качестве примера приведем упражнение по вычислению квартилей в ряду сгруппированных данных:

Чтобы вычислить первый квартиль, необходимо сначала определить интервал, в который он попадает. Для этого применим следующую формулу:

Таким образом, первый квартиль будет находиться в интервале, чья совокупная абсолютная частота сразу превышает 7,75, в данном случае это интервал [50,60), чья совокупная абсолютная частота равна 15. И как только мы узнаем интервал квартиля, мы используем вторую формулу процесса :

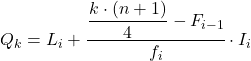
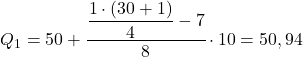
Мы применим ту же процедуру еще раз, чтобы получить второй квартиль. Сначала определяем интервал, в котором лежит квартиль:

Интервал, кумулятивная абсолютная частота которого сразу превышает 15,5, равен [60,70) с кумулятивной абсолютной частотой 26. Таким образом, второй квартиль равен:

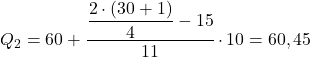
И, наконец, мы повторяем процесс, чтобы найти третий квартиль. Сначала вычислим интервал, содержащий квартиль:

Совокупная абсолютная частота непосредственно выше 23,25 равна 26, поэтому диапазон третьего квартиля равен [60,70). Поэтому мы применяем формулу для расчета квартиля с этим интервалом:

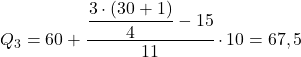
Для чего используются квартили?

Квартили — это мера положения, поэтому они используются для определения того, как позиционируются данные. Другими словами, значения трех квартилей позволяют нам узнать, является ли случайный элемент данных в выборке очень большим, очень маленьким или это среднее значение.

Если мы случайным образом возьмем часть данных из выборки, мы сможем определить, является ли ее значение высоким или низким, сравнив его с квартилями. Если значение случайных данных меньше первого квартиля, это будет небольшое значение, но если его значение больше третьего квартиля, это будет большое значение. Аналогично, если значение указанных данных находится между первым и третьим квартилем, это промежуточное значение.

С другой стороны, квартили также используются для расчета других статистических показателей, таких как межквартильный размах (или межквартильный размах), а также для построения диаграмм, таких как ящичковая диаграмма и диаграмма с усами (или ящичная диаграмма).