Как выполнить кубическую регрессию в python

Кубическая регрессия — это тип регрессии, который мы можем использовать для количественной оценки связи между переменной-предиктором и переменной ответа, когда связь между переменными нелинейна.

В этом руководстве объясняется, как выполнить кубическую регрессию в Python.

Пример: кубическая регрессия в Python

Предположим, у нас есть следующий DataFrame pandas, который содержит две переменные (x и y):

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

Если мы построим простую диаграмму рассеяния этих данных, мы увидим, что связь между двумя переменными нелинейна:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

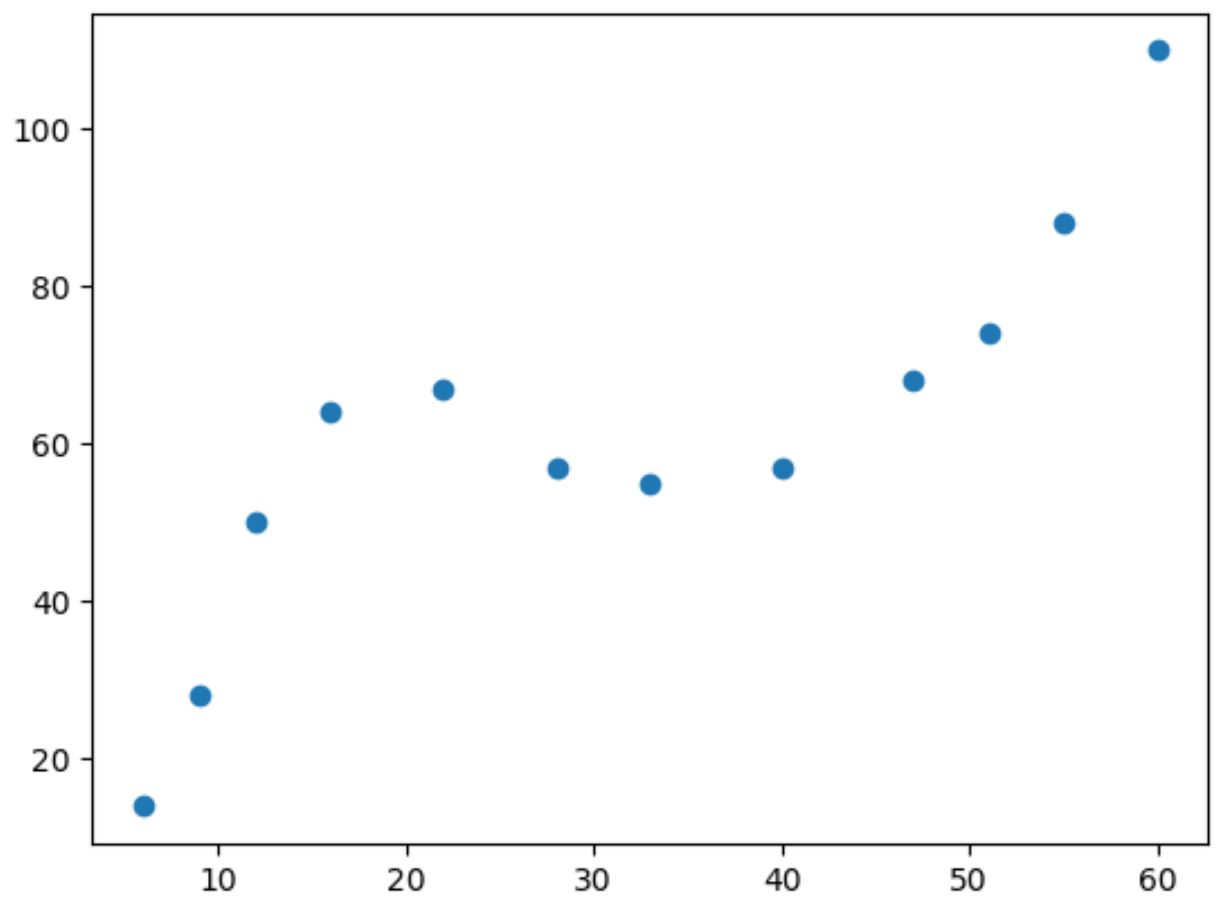
По мере увеличения значения x значение y увеличивается до определенной точки, затем уменьшается, а затем снова увеличивается.

Этот образец с двумя «кривыми» на графике указывает на кубическую зависимость между двумя переменными.

Это означает, что модель кубической регрессии является хорошим кандидатом для количественной оценки взаимосвязи между двумя переменными.

Чтобы выполнить кубическую регрессию, мы можем подогнать модель полиномиальной регрессии степени 3, используя функцию numpy.polyfit() :

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

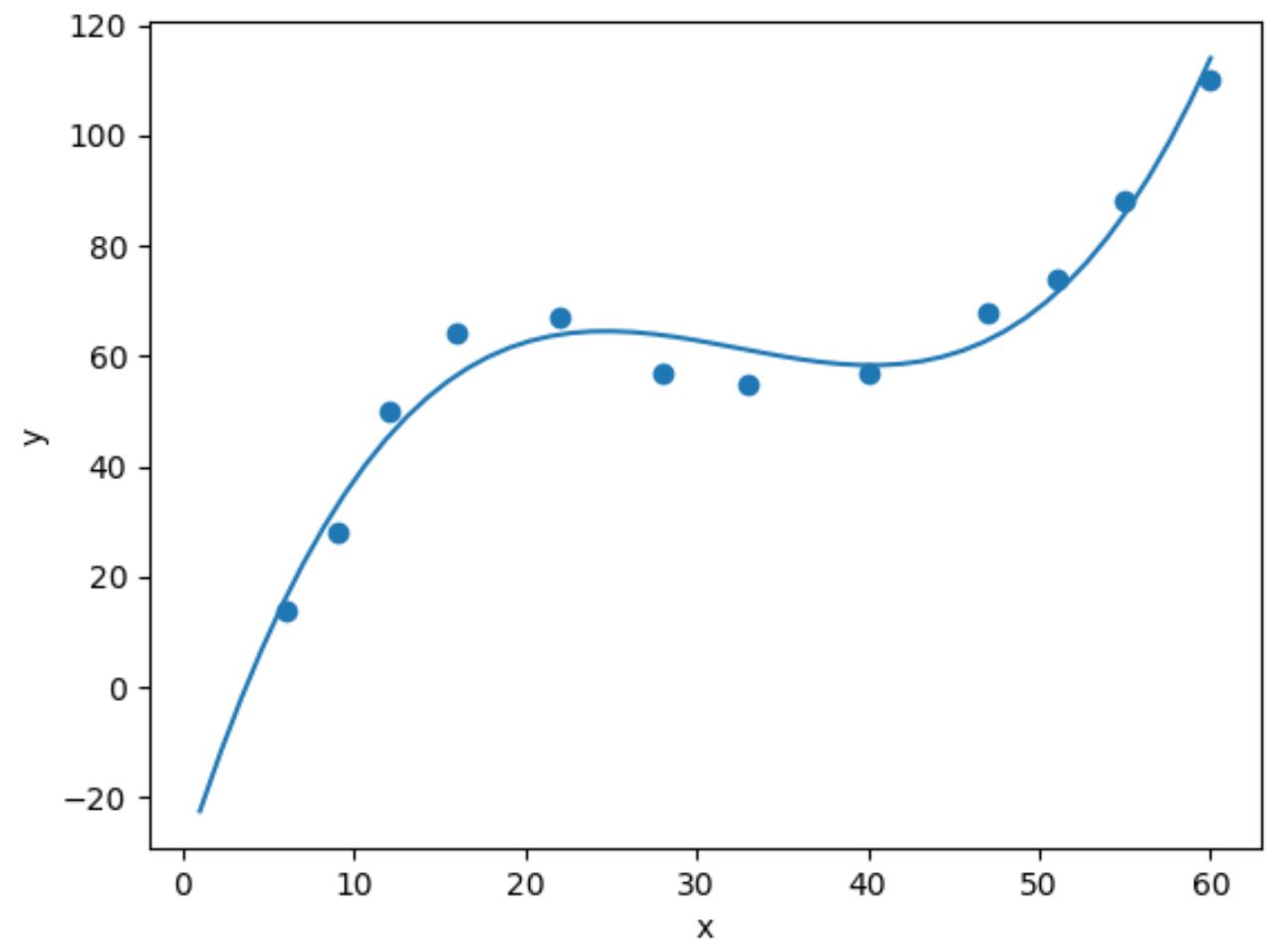
Мы можем получить подобранное уравнение кубической регрессии, распечатав коэффициенты модели:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

Подобранное уравнение кубической регрессии:

у = 0,003302(х) ³ – 0,3214(х) ² + 9,832х – 30,01

Мы можем использовать это уравнение для расчета ожидаемого значения y на основе значения x.

Например, если x равно 30, то ожидаемое значение y равно 64,844:

у = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

Мы также можем написать короткую функцию, чтобы получить R-квадрат модели, который представляет собой долю дисперсии переменной отклика, которую можно объяснить переменными-предикторами.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

В этом примере квадрат R модели равен 0,9632 .

Это означает, что 96,32% вариаций переменной отклика можно объяснить переменной-предиктором.

Поскольку это значение настолько велико, оно говорит нам о том, что модель кубической регрессии хорошо определяет количественно взаимосвязь между двумя переменными.

Связанный: Что такое хорошее значение R-квадрата?

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи на Python:

Как выполнить простую линейную регрессию в Python
Как выполнить квадратичную регрессию в Python
Как выполнить полиномиальную регрессию в Python