Введение в логистическую регрессию

Когда мы хотим понять взаимосвязь между одной или несколькими переменными-предикторами и переменной непрерывного отклика, мы часто используем линейную регрессию .

Однако, когда переменная ответа является категориальной, мы можем использовать логистическую регрессию .

Логистическая регрессия — это тип алгоритма классификации , поскольку он пытается «классифицировать» наблюдения в наборе данных по отдельным категориям.

Вот несколько примеров использования логистической регрессии:

• Мы хотим использовать кредитный рейтинг и банковский баланс , чтобы предсказать, не сможет ли данный клиент выплатить кредит. (Переменная ответа = «По умолчанию» или «Нет по умолчанию»)
• Мы хотим использовать среднее количество подборов за игру и среднее количество очков за игру , чтобы предсказать, будет ли данный баскетболист выбран в НБА (переменная ответа = «Драфт» или «Недрафт»).
• Мы хотим использовать квадратные метры и количество ванных комнат , чтобы предсказать, будет ли дом в определенном городе выставлен на продажу по цене 200 000 долларов или больше. (Переменная ответа = «Да» или «Нет»)

Обратите внимание, что переменная ответа в каждом из этих примеров может принимать только одно из двух значений. Сравните это с линейной регрессией, в которой переменная отклика принимает непрерывное значение.

Уравнение логистической регрессии

Логистическая регрессия использует метод, известный как оценка максимального правдоподобия (детали здесь не обсуждаются), чтобы найти уравнение следующей формы:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Золото:

• X _j : j- ^я прогнозируемая переменная
• β _j : оценка коэффициента для j ^-й прогнозируемой переменной

Формула в правой части уравнения предсказывает логарифмическую вероятность того, что переменная ответа примет значение 1.

Итак, когда мы подгоняем модель логистической регрессии, мы можем использовать следующее уравнение для расчета вероятности того, что данное наблюдение примет значение 1:

p(X) = e ^{β ₀ + β _{1 X 1 + β 2 X 2 + … + β p}}

Затем мы используем определенный порог вероятности, чтобы классифицировать наблюдение как 1 или 0.

Например, мы могли бы сказать, что наблюдения с вероятностью, большей или равной 0,5, будут классифицированы как «1», а все остальные наблюдения будут классифицированы как «0».

Как интерпретировать результат логистической регрессии

Предположим, мы используем модель логистической регрессии, чтобы предсказать, будет ли данный баскетболист выбран в НБА, на основе его среднего количества подборов за игру и среднего количества очков за игру.

Вот результат модели логистической регрессии:

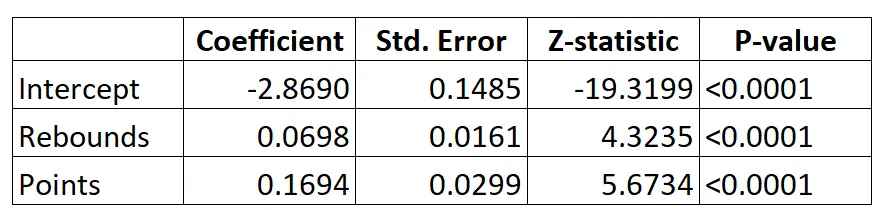
Используя коэффициенты, мы можем рассчитать вероятность того, что данный игрок будет выбран в НБА, исходя из его среднего количества подборов и очков за игру, используя следующую формулу:

P(Драфт) = e ^{-2,8690 + 0,0698*(ребы) + 0,1694*(очки)} / (1+e ^{-2,8690 + 0,0698*(ребы) + 0,1694*(очки) ) )}

Например, предположим, что данный игрок набирает в среднем 8 подборов за игру и 15 очков за игру. Согласно модели вероятность того, что этого игрока задрафтуют в НБА, равна 0,557 .

P(письменный) = e ^{-2,8690 + 0,0698*(8) + 0,1694*(15)} / (1+e ^{-2,8690 + 0,0698*(8) + 0,1694*(15)} ) = 0,557

Поскольку эта вероятность больше 0,5, мы прогнозируем, что этот игрок будет выбран на драфте.

Сравните это с игроком, который в среднем набирает всего 3 подбора и 7 очков за игру. Вероятность того, что этого игрока задрафтуют в НБА, равна 0,186 .

P(письменный) = e ^{-2,8690 + 0,0698*(3) + 0,1694*(7)} / (1+e ^{-2,8690 + 0,0698*(3) + 0,1694*(7 )} ) = 0,186

Поскольку эта вероятность меньше 0,5, мы прогнозируем, что этот игрок не будет выбран на драфте.

Предположения логистической регрессии

Логистическая регрессия использует следующие предположения:

1. Переменная ответа является двоичной. Предполагается, что переменная ответа может принимать только два возможных результата.

2. Наблюдения независимы. Предполагается, что наблюдения в наборе данных независимы друг от друга. То есть наблюдения не должны основываться на повторных измерениях одного и того же человека или каким-либо образом быть связаны друг с другом.

3. Между переменными-предикторами нет серьезной мультиколлинеарности . Предполагается, что ни одна из переменных-предикторов не сильно коррелирует друг с другом.

4. Никаких резких выбросов нет. Предполагается, что в наборе данных нет экстремальных выбросов или влиятельных наблюдений.

5. Существует линейная зависимость между переменными-предикторами и логитом переменной отклика . Эту гипотезу можно проверить с помощью теста Бокса-Тидвелла.

6. Размер выборки достаточно велик. Обычно для каждой объясняющей переменной должно быть минимум 10 случаев с наименее частым исходом. Например, если у вас есть 3 объясняющие переменные и ожидаемая вероятность наименее частого результата равна 0,20, то размер выборки должен быть не менее (10*3)/0,20 = 150.

Прочтите эту статью для подробного объяснения того, как проверить эти предположения.