Логистическая регрессия
В этой статье объясняется, что такое логистическая регрессия в статистике. Кроме того, вы найдете формулу логистической регрессии, различные типы логистической регрессии и, кроме того, решаемое упражнение логистической регрессии.
Что такое логистическая регрессия?
В статистике логистическая регрессия — это тип регрессионной модели, используемый для прогнозирования результата категориальной переменной . То есть логистическая регрессия используется для моделирования вероятности того, что категориальная переменная примет определенное значение на основе независимых переменных.
Наиболее распространенной моделью логистической регрессии является бинарная логистическая регрессия, в которой есть только два возможных результата: «неудача» или «успех» ( распределение Бернулли ). «Неудача» представлена значением 0, а «успех» — значением 1.
Например, вероятность сдачи студентом экзамена на основе часов, потраченных на обучение, можно изучить с помощью модели логистической регрессии. В этом случае неудача была бы результатом «неудачи» и, с другой стороны, успех был бы результатом «успеха».
Формула логистической регрессии
Уравнение модели логистической регрессии:
![]()
Поэтому в модели логистической регрессии вероятность получения «успешного» результата, то есть того, что зависимая переменная примет значение 1, рассчитывается по следующей формуле:
![]()
Золото:
-

— вероятность того, что зависимая переменная равна 1.
-

— константа модели логистической регрессии.
-

– коэффициент регрессии переменной i.
-

значение переменной i.
Пример модели логистической регрессии
Теперь, когда мы знаем определение логистической регрессии, давайте посмотрим на конкретный пример того, как создать модель этого типа регрессии.
- В следующей таблице собрана серия из 20 данных, которые касаются учебных часов каждого студента и того, сдали ли они статистический экзамен или не сдали его. Запустите модель логистической регрессии и рассчитайте вероятность того, что студент сдаст экзамен, если он проучился 4 часа.
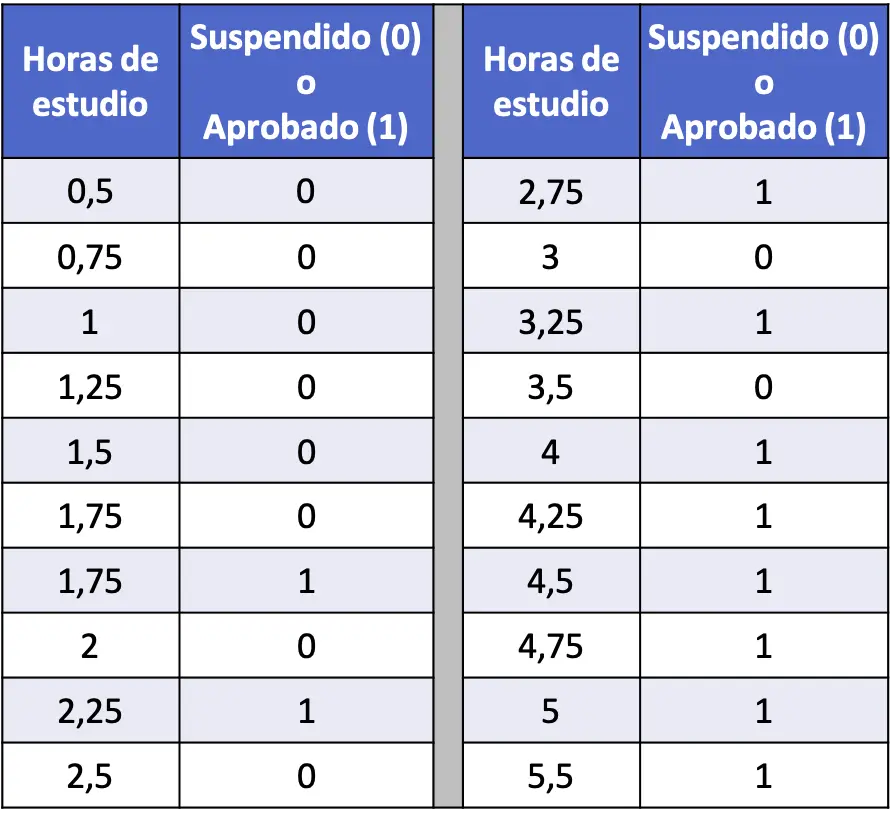
В этом случае объясняющая переменная — это количество часов обучения, а переменная ответа — провалил ли студент (0) или сдал экзамен (1). Поэтому в нашей модели мы будем иметь только коэффициент
![]()
и коэффициент
![]()
, поскольку существует только одна независимая переменная.
![]()
Ручное определение коэффициентов регрессии очень трудоемко, поэтому рекомендуется использовать компьютерное программное обеспечение, например Minitab. Таким образом, значения коэффициентов регрессии, рассчитанные с помощью Minitab, следующие:
![Rendered by QuickLaTeX.com \begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6ed66de602220c69aabb71a726fec9f8_l3.png)
Таким образом, модель логистической регрессии выглядит следующим образом:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0902ac67194bedf38d5f4ff06dc27a38_l3.png)
Ниже вы можете увидеть примеры данных и графическое уравнение модели логистической регрессии:
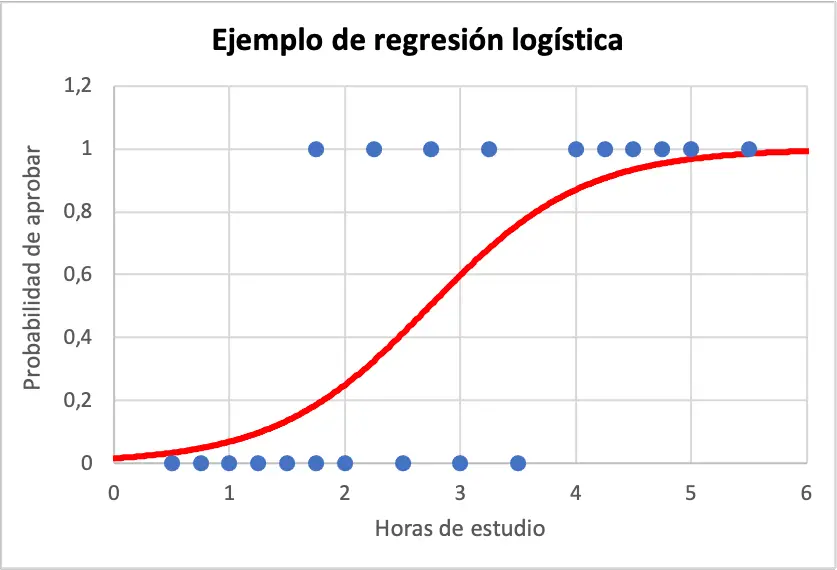
Таким образом, чтобы рассчитать вероятность того, что студент добьется успеха, если он проучился 4 часа, просто используйте уравнение, полученное из модели логистической регрессии:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-930691eafee62c04e59d9c4de8ef6a76_l3.png)
Короче говоря, если студент учится четыре часа, вероятность сдать экзамен у него будет 86,99%.
Типы логистической регрессии
Существует три типа логистической регрессии :
- Бинарная логистическая регрессия : зависимая переменная может иметь только два значения (0 и 1).
- Полиномиальная логистическая регрессия : зависимая переменная имеет более двух возможных значений.
- Порядковая логистическая регрессия : возможные результаты имеют естественный порядок.
Логистическая регрессия и линейная регрессия
Наконец, подводя итог, мы увидим, в чем разница между логистической регрессией и линейной регрессией, поскольку наиболее используемой моделью регрессии в статистике является линейная модель.
Линейная регрессия используется для моделирования числовых зависимых переменных. Кроме того, в линейной регрессии связь между объясняющими переменными и переменной ответа является линейной.
Следовательно, основное различие между логистической регрессией и линейной регрессией заключается в типе зависимой переменной. В логистической регрессии зависимая переменная является категориальной, тогда как зависимая переменная в линейной регрессии является числовой.
Таким образом, логистическая регрессия используется для прогнозирования результата между двумя возможными вариантами, а линейная регрессия помогает прогнозировать численный результат.