Межквартильный размах (или межквартильный размах)

В этой статье объясняется, что такое межквартильный размах, также известный как межквартильный размах. Вы также сможете увидеть, как рассчитывается межквартильный размах, на конкретном примере. Вы узнаете, что такое межквартильный размах и чем отличается интервал. Кроме того, вы можете рассчитать межквартильный размах любого набора данных с помощью онлайн-калькулятора.

Что такое интерквартильный (или интерквартильный) размах?

Межквартильный размах, также называемый межквартильным размахом, представляет собой меру статистической дисперсии, которая указывает на разницу между третьим и первым квартилем. Следовательно, чтобы вычислить межквартильный размах набора статистических данных, необходимо сначала найти третий и первый квартиль, а затем вычесть их.

Вкратце, межквартильный размах обозначается аббревиатурой IQR.

Одной из наиболее выгодных характеристик межквартильного размаха является то, что это устойчивая статистика, то есть она имеет высокую устойчивость к выбросам. Поскольку крайние значения не учитываются при расчете межквартильного размаха, его значение будет меняться очень незначительно в случае появления новых выбросов .

Очевидно, что помимо межквартильного размаха существуют и другие меры дисперсии. Наиболее известными показателями являются размах, дисперсия, стандартное (или стандартное) отклонение, среднее отклонение и коэффициент вариации.

Как рассчитать интерквартильный (или межквартильный) размах

В статистике, чтобы вычислить межквартильный размах (или межквартильный размах) набора данных, вы должны сначала найти первый и третий квартиль набора данных, а затем вычислить вычитание третьего квартиля минус первый квартиль.

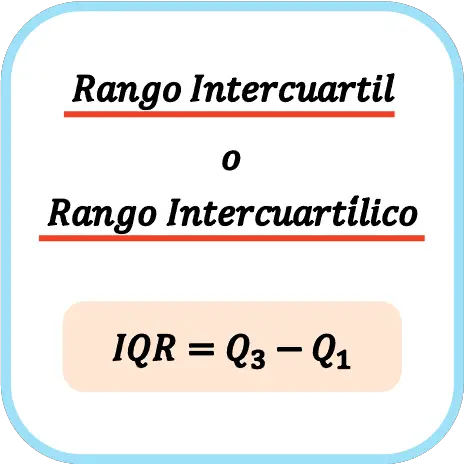
Следовательно, формула расчета интерквартильного размаха или межквартильного размаха такова:

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать межквартильный размах для любого набора данных.

Поэтому очень важно знать, как рассчитываются квартили статистической выборки. Вот почему я рекомендую вам, прежде чем продолжить, ознакомиться со следующей статьей, а затем продолжить объяснение.

Пример интерквартильного (или межквартильного) размаха

Учитывая определение и формулу межквартильного размаха (или межквартильного размаха), ниже приведено решенное упражнение, чтобы вы могли точно увидеть, как рассчитывается этот тип меры дисперсии.

• Мы хотим статистически проанализировать, стоит ли инвестировать в компанию. Для этого мы собрали данные о цене акций этой компании за последние 15 месяцев. В следующей таблице вы можете увидеть наблюдаемые данные, упорядоченные от наименьшего к наибольшему. Рассчитайте межквартильный диапазон для этого набора данных.

Как мы видели в предыдущем разделе, чтобы получить межквартильный размах (или межквартильный размах) выборки, мы должны сначала вычислить первый и третий квартиль.

Первый квартиль представляет собой медиану первой половины значений, что соответствует 8,95 евро/акция.

С другой стороны, третий квартиль представляет собой промежуточное значение второй половины значений, поэтому он составляет 9,83 евро/акция.

Итак, чтобы найти межквартильный размах, просто примените формулу и вычтите третий квартиль минус первый квартиль.

Калькулятор межквартильного (или межквартильного) диапазона

Введите набор статистических данных в следующий калькулятор, чтобы рассчитать его межквартильный размах или межквартильный размах. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Разница между межквартильным размахом и размахом

В статистике разницей между межквартильным размахом (или межквартильным размахом) и интервалом являются значения, которые принимаются для выполнения расчета. Межквартильный размах – это разница между третьим и первым квартилем, а размах – это разница между крайними значениями выборки.

Таким образом, межквартильный диапазон измеряет дисперсию выборки с использованием центральных данных, а интервал определяет количественную дисперсию выборки с использованием крайних данных.

Следовательно, на статистический диапазон гораздо больше влияют выбросы , поскольку они обычно представляют собой минимум или максимум набора данных. Таким образом, одним из преимуществ межквартильного размаха перед интервалом является его большая устойчивость.

Для чего используется интерквартильный (или межквартильный) размах?

В первую очередь межквартильный размах (или межквартильный размах) используется для измерения распределения набора данных . полностью Хотя анализ дисперсии выборки требует расчета большего числа статистических показателей, межквартильный размах дает представление о том, насколько дисперсна выборка, по крайней мере, по центральным значениям.

Таким образом, интерпретация межквартильного размаха относительно проста. Чем выше значение межквартильного размаха, тем более разбросаны средние данные в выборке, а чем меньше межквартильный размах, тем ближе друг к другу находятся средние данные.

Кроме того, межквартильный диапазон также полезен для создания диаграммы «коробка с усами» — широко используемой диаграммы для анализа поведения цен акций на фондовом рынке.