Пять предположений множественной линейной регрессии

Множественная линейная регрессия — это статистический метод, который мы можем использовать, чтобы понять взаимосвязь между несколькими переменными-предикторами и переменной отклика .

Однако прежде чем выполнять множественную линейную регрессию, мы должны сначала убедиться, что выполняются пять допущений:

1. Линейная связь. Между каждой переменной-предиктором и переменной отклика существует линейная связь.

2. Отсутствие мультиколлинеарности: ни одна из переменных-предсказателей не имеет высокой корреляции друг с другом.

3. Независимость: наблюдения независимы.

4. Гомоскедастичность: остатки имеют постоянную дисперсию в каждой точке линейной модели.

5. Многомерная нормальность: остатки модели имеют нормальное распределение.

Если одно или несколько из этих допущений не выполняются, результаты множественной линейной регрессии могут оказаться ненадежными.

В этой статье мы даем объяснение каждому предположению, как определить, выполняется ли предположение, и что делать, если предположение не выполняется.

Гипотеза 1: Линейная зависимость

Множественная линейная регрессия предполагает, что существует линейная связь между каждой переменной-предиктором и переменной ответа.

Как определить, выполняется ли это предположение

Самый простой способ определить, выполняется ли это предположение, — создать диаграмму рассеяния каждой переменной-предиктора и переменной отклика.

Это позволяет визуально увидеть, существует ли линейная связь между двумя переменными.

Если точки на диаграмме рассеяния лежат примерно вдоль прямой диагональной линии, вероятно, между переменными существует линейная связь.

Например, точки на графике ниже кажутся расположенными на прямой линии, что указывает на наличие линейной зависимости между этой конкретной переменной-предиктором (x) и переменной отклика (y):

Что делать, если это предположение не соблюдается

Если между одной или несколькими переменными-предикторами и переменной отклика нет линейной зависимости, то у нас есть несколько вариантов:

1. Примените нелинейное преобразование к переменной-предиктору, например, извлекая логарифмический или квадратный корень. Это часто может превратить отношения в более линейные.

2. Добавьте в модель еще одну переменную-предиктор. Например, если график зависимости x от y имеет параболическую форму, возможно, имеет смысл добавить X ² в качестве дополнительной переменной-предиктора в модели.

3. Удалите переменную-предиктор из модели. В самом крайнем случае, если между определенной переменной-предиктором и переменной отклика нет линейной зависимости, включение переменной-предиктора в модель может оказаться бесполезным.

Гипотеза 2: мультиколлинеарности нет.

Множественная линейная регрессия предполагает, что ни одна из переменных-предикторов не сильно коррелирует друг с другом.

Когда одна или несколько переменных-предикторов сильно коррелируют, регрессионная модель страдает от мультиколлинеарности , что делает оценки коэффициентов модели ненадежными.

Как определить, выполняется ли это предположение

Самый простой способ определить, выполняется ли это предположение, — вычислить значение VIF для каждой переменной-предиктора.

Значения VIF начинаются с 1 и не имеют верхнего предела. Как правило, значения VIF выше 5* указывают на потенциальную мультиколлинеарность.

В следующих руководствах показано, как рассчитать VIF в различных статистических программах:

• Как рассчитать VIF в R
• Как рассчитать VIF в Python
• Как рассчитать VIF в Excel

*Иногда исследователи вместо этого используют значение VIF, равное 10, в зависимости от области исследования.

Что делать, если это предположение не соблюдается

Если одна или несколько переменных-предикторов имеют значение VIF больше 5, самый простой способ решить эту проблему — просто удалить переменные-предикторы с высокими значениями VIF.

В качестве альтернативы, если вы хотите сохранить каждую переменную-предиктор в модели, вы можете использовать другой статистический метод, такой какрегрессия гребня , регрессия лассо или регрессия частичных наименьших квадратов , предназначенный для обработки сильно коррелированных переменных-предикторов.

Гипотеза 3: Независимость

Множественная линейная регрессия предполагает, что каждое наблюдение в наборе данных независимо.

Как определить, выполняется ли это предположение

Самый простой способ определить, выполняется ли это предположение, — выполнить тест Дурбина-Ватсона , который представляет собой формальный статистический тест, который сообщает нам, проявляют ли остатки (и, следовательно, наблюдения) автокорреляцию.

Что делать, если это предположение не соблюдается

В зависимости от того, насколько это предположение нарушается, у вас есть несколько вариантов:

• Для положительной серийной корреляции рассмотрите возможность добавления в модель лагов зависимой и/или независимой переменной.
• Для отрицательной последовательной корреляции убедитесь, что ни одна из ваших переменных не имеет чрезмерной задержки .
• Для сезонной корреляции рассмотрите возможность добавления в модель сезонных переменных .

Гипотеза 4: гомоскедастичность

Множественная линейная регрессия предполагает, что остатки имеют постоянную дисперсию в каждой точке линейной модели. Когда это не так, остатки страдают от гетероскедастичности .

Когда в регрессионном анализе присутствует гетероскедастичность, результаты регрессионной модели становятся ненадежными.

В частности, гетероскедастичность увеличивает дисперсию оценок коэффициента регрессии, но модель регрессии ее не учитывает. Это значительно повышает вероятность того, что регрессионная модель будет утверждать, что термин в модели является статистически значимым, хотя на самом деле это не так.

Как определить, выполняется ли это предположение

Самый простой способ определить, выполняется ли это предположение, — построить график сравнения стандартизированных остатков с прогнозируемыми значениями.

После того, как вы подгоните модель регрессии к набору данных, вы можете создать диаграмму рассеяния, которая отображает прогнозируемые значения переменной отклика по оси X и стандартизированные остатки модели по оси X. й.

Если точки на диаграмме рассеяния демонстрируют тенденцию, то присутствует гетероскедастичность.

На следующей диаграмме показан пример регрессионной модели, в которой гетероскедастичность не является проблемой:

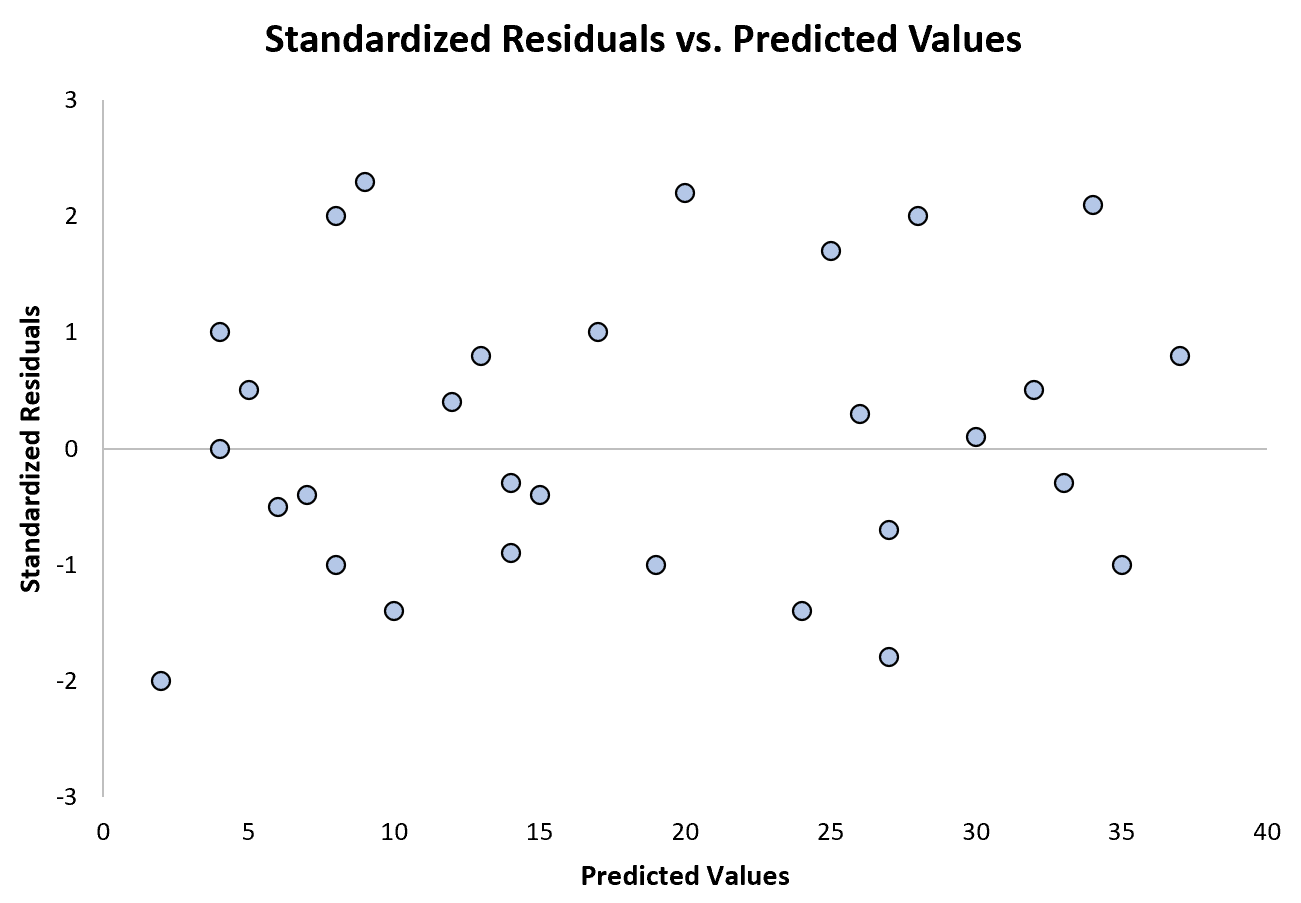
Обратите внимание, что стандартизованные остатки разбросаны вокруг нуля без четкой закономерности.

На следующей диаграмме показан пример регрессионной модели, в которой гетероскедастичность является проблемой:

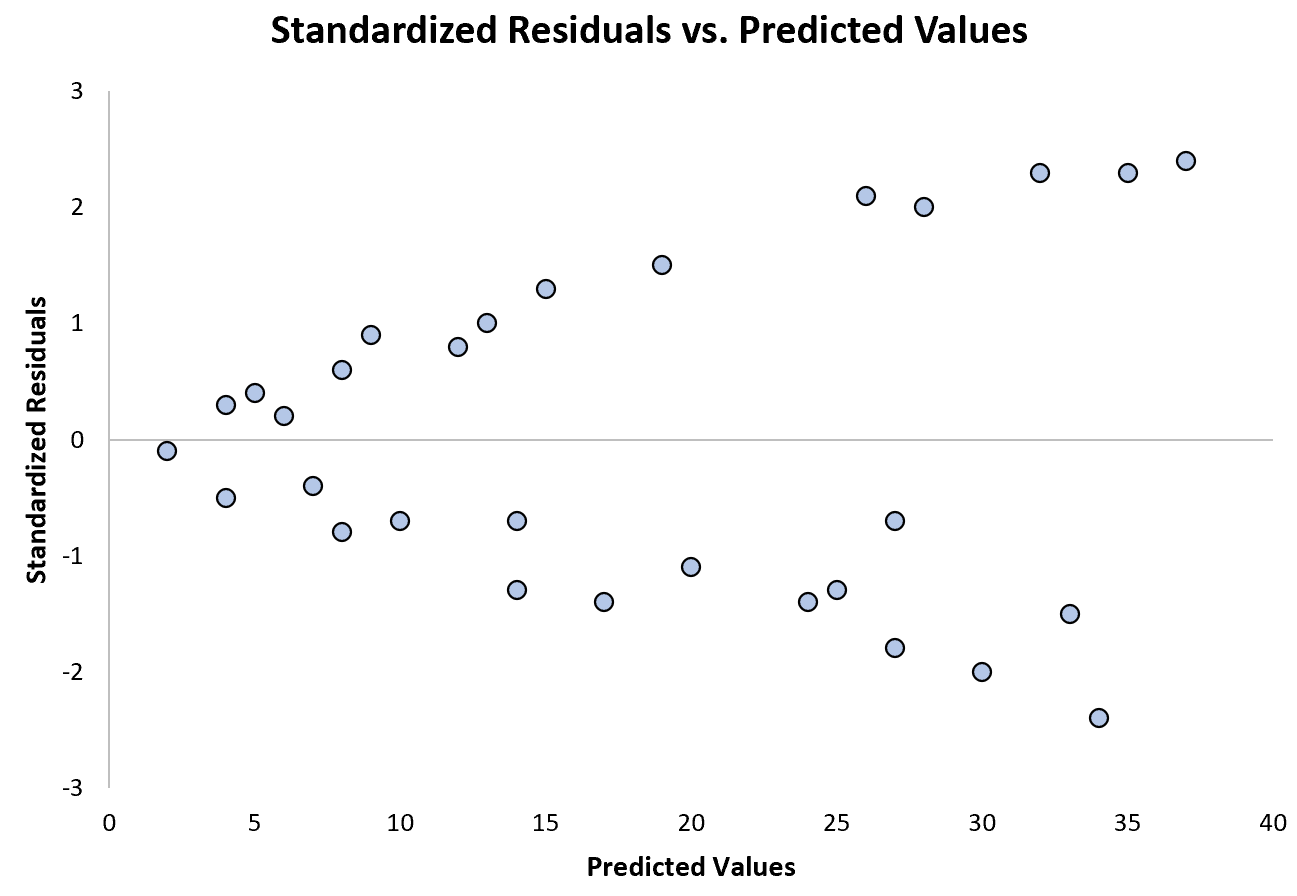
Обратите внимание, как стандартизированные остатки все больше и больше распределяются по мере увеличения прогнозируемых значений. Эта форма «конуса» является классическим признаком гетероскедастичности:

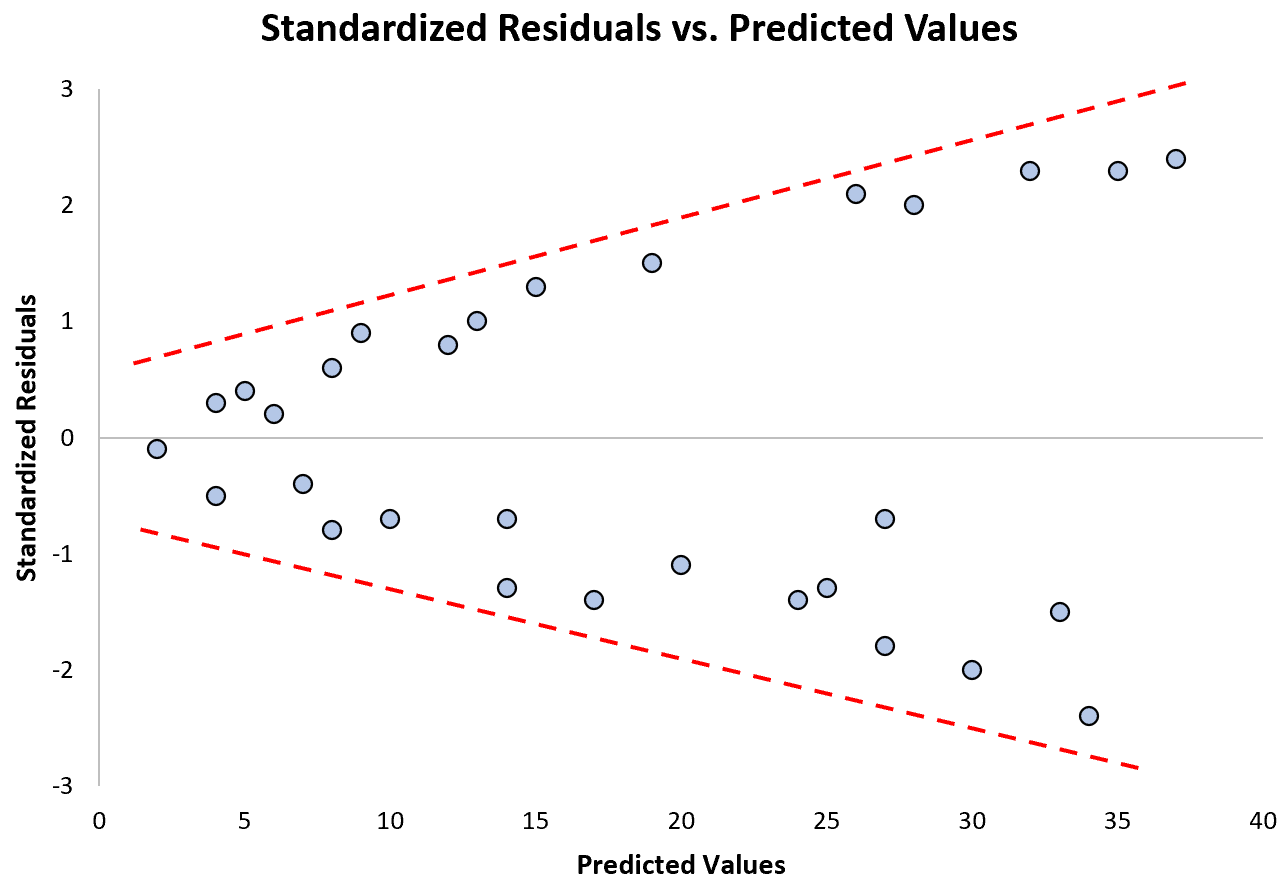
Что делать, если это предположение не соблюдается

Существует три распространенных способа коррекции гетероскедастичности:

1. Преобразуйте переменную ответа. Самый распространенный способ борьбы с гетероскедастичностью — преобразовать переменную отклика, взяв логарифмический, квадратный или кубический корень из всех значений переменной отклика. Зачастую это приводит к исчезновению гетероскедастичности.

2. Переопределите переменную ответа. Один из способов переопределить переменную ответа — использовать скорость , а не необработанное значение. Например, вместо того, чтобы использовать размер населения для прогнозирования количества флористов в городе, мы можем использовать размер населения для прогнозирования количества флористов на душу населения.

В большинстве случаев это уменьшает изменчивость, которая естественным образом возникает в больших популяциях, поскольку мы измеряем количество флористов на человека, а не количество флористов само по себе.

3. Используйте взвешенную регрессию. Другой способ исправить гетероскедастичность — использовать взвешенную регрессию, которая присваивает вес каждой точке данных на основе дисперсии ее подобранного значения.

По сути, это придает низкий вес точкам данных с более высокими дисперсиями, уменьшая их остаточные квадраты. Использование соответствующих весов может устранить проблему гетероскедастичности.

Связанный : Как выполнить взвешенную регрессию в R

Предположение 4: Многомерная нормальность

Множественная линейная регрессия предполагает, что остатки модели имеют нормальное распределение.

Как определить, выполняется ли это предположение

Есть два распространенных способа проверить, выполняется ли это предположение:

1. Визуально проверьте гипотезу, используя графики QQ .

График QQ, сокращение от графика квантиль-квантиль, — это тип графика, который мы можем использовать, чтобы определить, соответствуют ли остатки модели нормальному распределению. Если точки на графике примерно образуют прямую диагональную линию, то предположение о нормальности выполнено.

На следующем графике QQ показан пример остатков, который примерно соответствует нормальному распределению:

Однако график QQ ниже показывает пример случая, когда остатки явно отклоняются от прямой диагональной линии, что указывает на то, что они не соответствуют нормальному распределению:

2. Проверьте гипотезу, используя формальный статистический тест, такой как Шапиро-Уилк, Колмогоров-Смиронов, Жарк-Барре или Д’Агостино-Пирсон.

Имейте в виду, что эти тесты чувствительны к большим размерам выборки — то есть они часто приходят к выводу, что остатки не являются нормальными, когда размер вашей выборки чрезвычайно велик. Вот почему для проверки этой гипотезы зачастую проще использовать графические методы, такие как график QQ.

Что делать, если это предположение не соблюдается

Если предположение о нормальности не выполняется, у вас есть несколько вариантов:

1. Во-первых, убедитесь, что в данных нет экстремальных выбросов, которые приводят к нарушению предположения о нормальности.

2. Затем к переменной ответа можно применить нелинейное преобразование, например, извлекая квадратный, логарифмический или кубический корень из всех значений переменной ответа. Это часто приводит к более нормальному распределению остатков модели.

Дополнительные ресурсы

В следующих руководствах представлена дополнительная информация о множественной линейной регрессии и ее предположениях:

Введение в множественную линейную регрессию
Руководство по гетероскедастичности в регрессионном анализе
Руководство по мультиколлинеарности и VIF в регрессии

В следующих руководствах представлены пошаговые примеры выполнения множественной линейной регрессии с использованием различного статистического программного обеспечения:

Как выполнить множественную линейную регрессию в Excel
Как выполнить множественную линейную регрессию в R
Как выполнить множественную линейную регрессию в SPSS
Как выполнить множественную линейную регрессию в Stata