Как проверить мультиколлинеарность в spss
Мультиколлинеарность в регрессионном анализе возникает, когда две или более переменных-предикторов сильно коррелируют друг с другом, так что они не предоставляют уникальную или независимую информацию в модели регрессии. Если степень корреляции между переменными достаточно высока, это может вызвать проблемы при подборе и интерпретации регрессионной модели.
Один из способов обнаружить мультиколлинеарность — использовать метрику, известную как коэффициент инфляции дисперсии (VIF) , который измеряет корреляцию и силу корреляции между переменными-предикторами в регрессионной модели.
В этом руководстве объясняется, как использовать VIF для обнаружения мультиколлинеарности в регрессионном анализе в SPSS.
Пример: мультиколлинеарность в SPSS
Предположим, у нас есть следующий набор данных, который показывает экзаменационные баллы 10 студентов, а также количество часов, которые они потратили на обучение, количество сданных практических экзаменов и их текущую оценку по курсу:
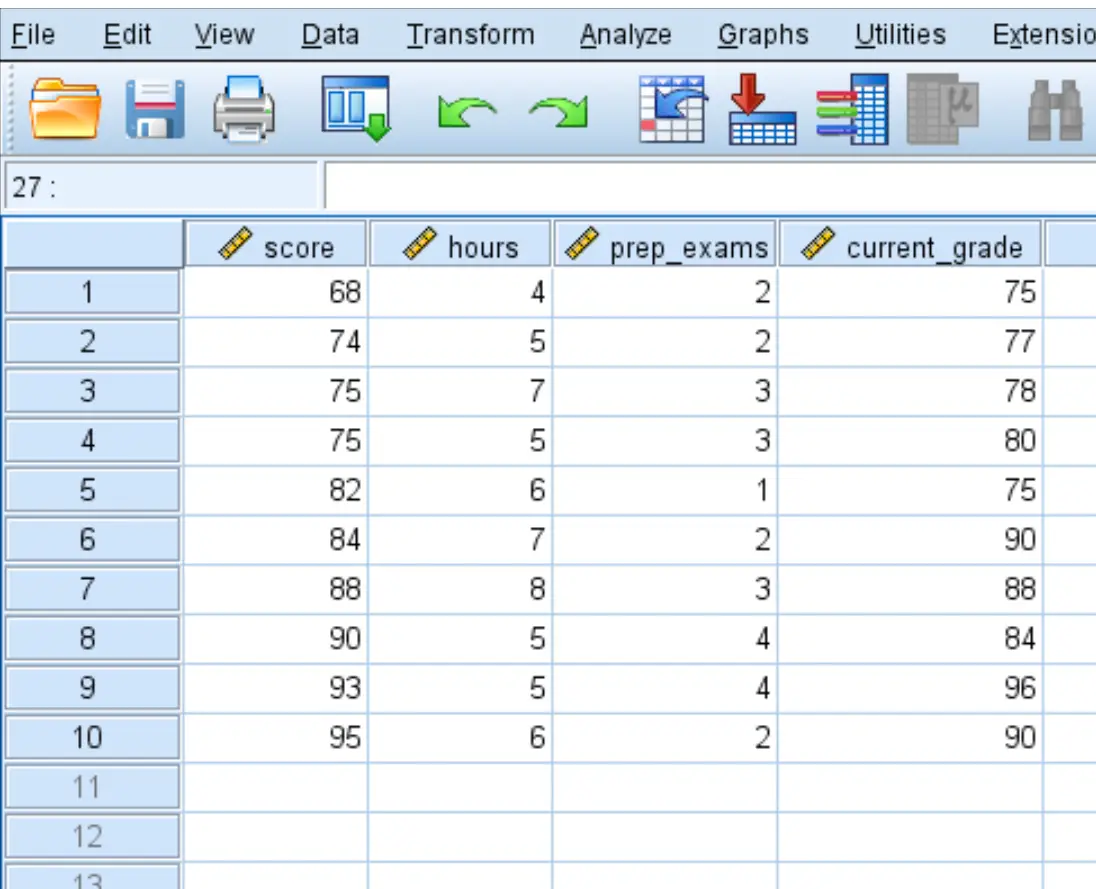
Мы хотели бы выполнить линейную регрессию, используя счет в качестве переменной ответа и часы , prep_exams и current_grade в качестве переменных-предикторов, но мы хотим убедиться, что три переменные-предиктора не сильно коррелируют.
Чтобы определить, является ли мультиколлинеарность проблемой, мы можем получить значения VIF для каждой из переменных-предикторов.
Для этого нажмите вкладку «Анализ» , затем «Регрессия» , затем «Линейный» :
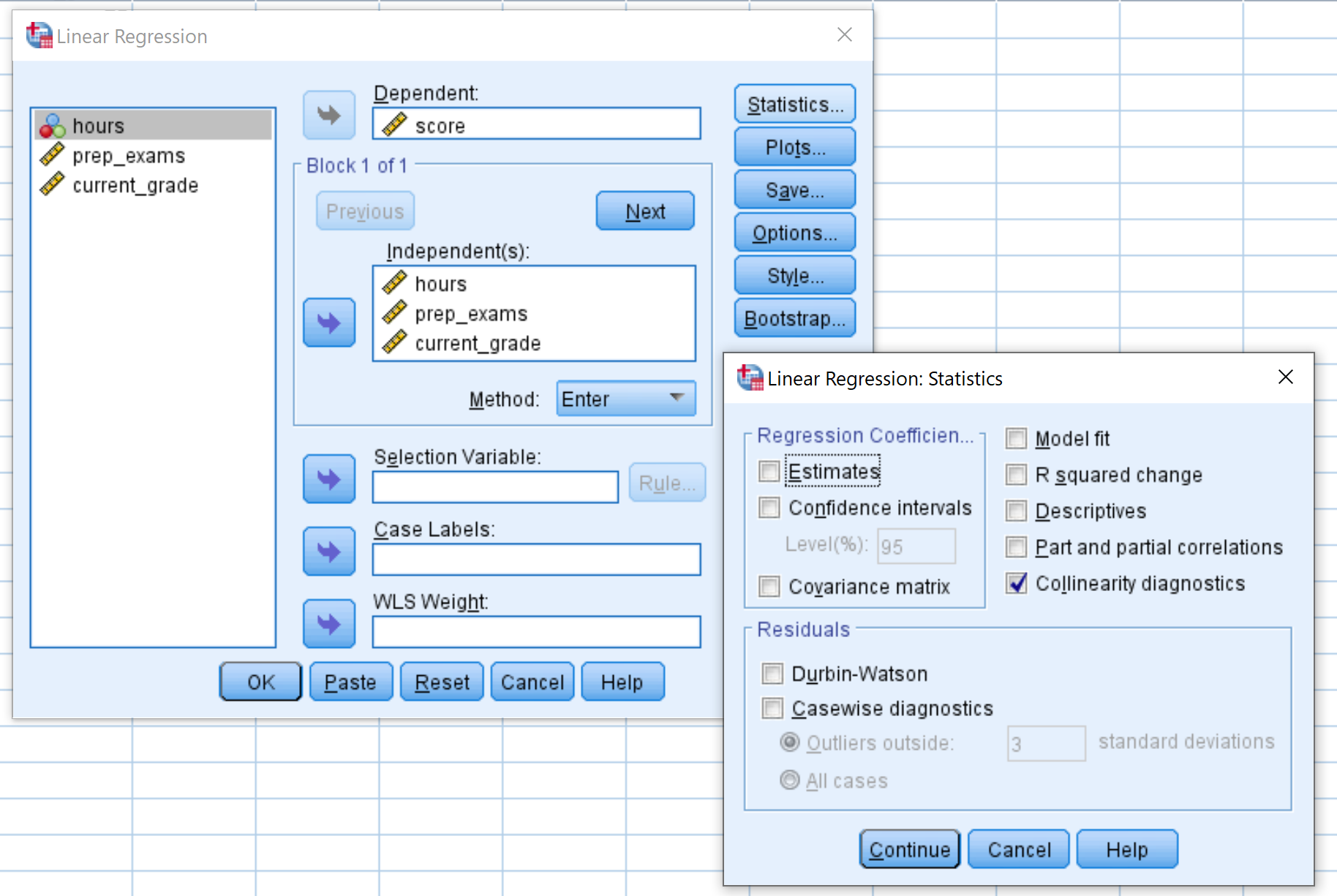
В появившемся новом окне перетащите оценку в поле с надписью «Зависимые» и перетащите три переменные-предикторы в поле с надписью «Независимые». Затем нажмите «Статистика» и убедитесь, что рядом с «Диагностика коллинеарности» установлен флажок. Затем нажмите Продолжить . Затем нажмите ОК .
После того, как вы нажмете «ОК» , появится следующая таблица, показывающая значение VIF для каждой предикторной переменной:
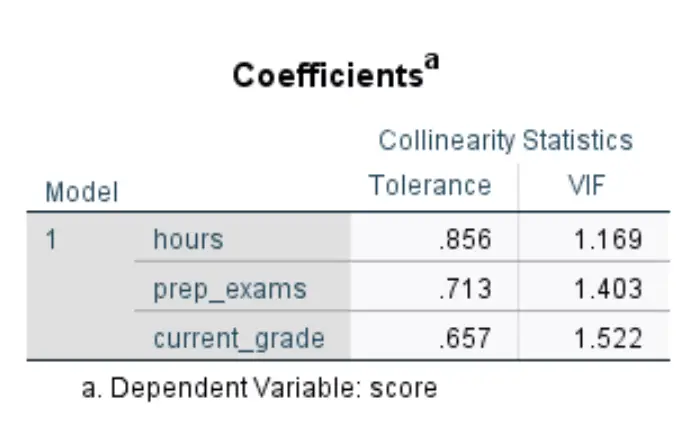
Значения VIF для каждой из переменных-предикторов следующие:
- часы: 1169
- prep_exams: 1,403
- текущий_балл: 1,522
Значение VIF начинается с 1 и не имеет верхнего предела. Общее правило интерпретации VIF следующее:
- Значение 1 указывает на отсутствие корреляции между данной переменной-предиктором и любой другой переменной-предиктором в модели.
- Значение от 1 до 5 указывает на умеренную корреляцию между данной переменной-предиктором и другими переменными-предикторами в модели, но часто она недостаточно серьезна, чтобы требовать особого внимания.
- Значение больше 5 указывает на потенциально серьезную корреляцию между данной переменной-предиктором и другими переменными-предикторами в модели. В этом случае оценки коэффициентов и значения p в результатах регрессии, скорее всего, ненадежны.
Мы видим, что ни одно из значений VIF для переменных-предикторов в этом примере не превышает 5, что указывает на то, что мультиколлинеарность не будет проблемой в регрессионной модели.