Как использовать надежные стандартные ошибки в регрессии в stata

Множественная линейная регрессия — это метод, который мы можем использовать, чтобы понять взаимосвязь между несколькими объясняющими переменными и переменной отклика.

К сожалению, проблема, которая часто возникает в регрессии, известна как гетероскедастичность , при которой происходит систематическое изменение дисперсии остатков в диапазоне измеренных значений.

Это приводит к увеличению дисперсии оценок коэффициента регрессии, но регрессионная модель это не учитывает. Это значительно повышает вероятность того, что регрессионная модель будет утверждать, что термин в модели является статистически значимым, хотя на самом деле это не так.

Один из способов объяснить эту проблему — использовать надежные стандартные ошибки , которые более «устойчивы» к проблеме гетероскедастичности и имеют тенденцию обеспечивать более точную меру истинной стандартной ошибки коэффициента регрессии.

В этом руководстве объясняется, как использовать надежные стандартные ошибки в регрессионном анализе в Stata.

Пример: надежные стандартные ошибки в Stata

Мы будем использовать автоматически интегрированный набор данных Stata, чтобы проиллюстрировать, как использовать надежные стандартные ошибки в регрессии.

Шаг 1: Загрузите и отобразите данные.

Сначала используйте следующую команду для загрузки данных:

автоматическое использование системы

Затем отобразите необработанные данные с помощью следующей команды:

бр

Шаг 2. Выполните множественную линейную регрессию без надежных стандартных ошибок.

Далее мы введем следующую команду, чтобы выполнить множественную линейную регрессию, используя цену в качестве переменной ответа, а миль на галлон и вес в качестве объясняющих переменных:

регрессионная цена, вес миль на галлон

Шаг 3. Выполните множественную линейную регрессию, используя надежные стандартные ошибки.

Теперь мы выполним ту же самую множественную линейную регрессию, но на этот раз мы будем использовать команду vce(robust) , чтобы Stata знала, как использовать надежные стандартные ошибки:

регрессионная цена, вес миль на галлон, vce (робастный)

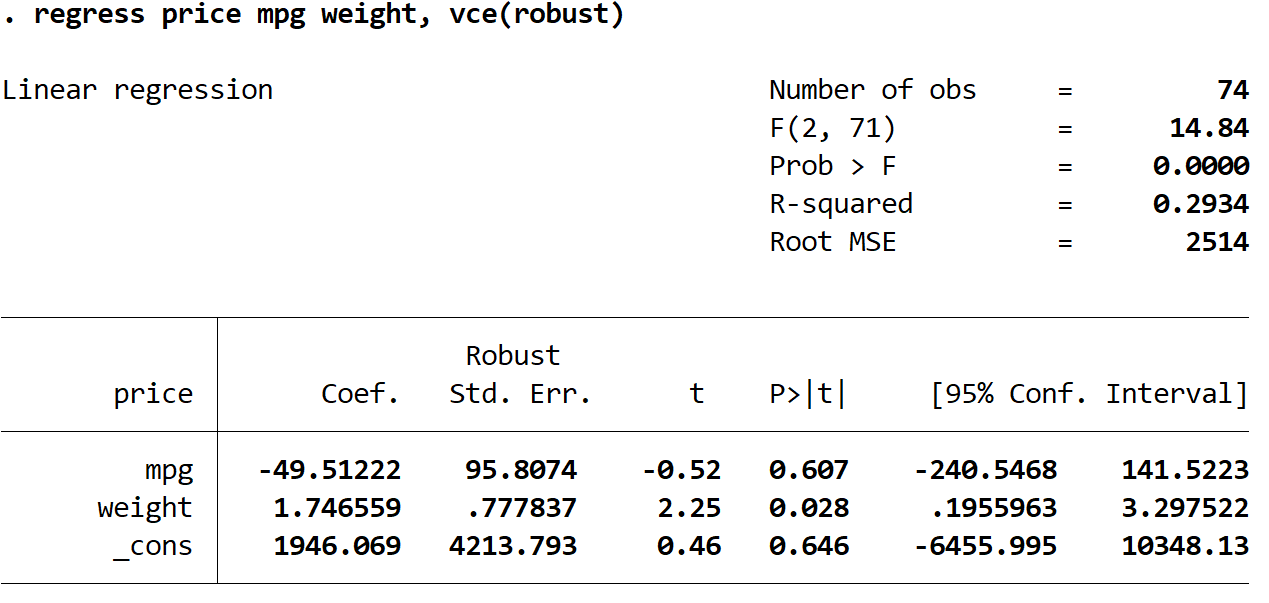
Здесь следует отметить несколько интересных вещей:

1. Оценки коэффициентов остались прежними . Когда мы используем устойчивые стандартные ошибки, оценки коэффициентов вообще не меняются. Обратите внимание, что оценки коэффициентов для миль на галлон, веса и константы для обеих регрессий следующие:

• миль на галлон: -49,51222
• вес: 1,746559
• _против: 1946.069

2. Изменились стандартные ошибки . Обратите внимание, что когда мы использовали надежные стандартные ошибки, стандартные ошибки для каждой из оценок коэффициентов увеличивались.

Примечание. В большинстве случаев устойчивые стандартные ошибки будут больше, чем обычные стандартные ошибки, но в редких случаях возможно, что устойчивые стандартные ошибки на самом деле будут меньше.

3. Изменилась тестовая статистика каждого коэффициента. Обратите внимание, что абсолютное значение каждой тестовой статистики t уменьшилось. По сути, статистика теста рассчитывается как расчетный коэффициент, разделенный на стандартную ошибку. Таким образом, чем больше стандартная ошибка, тем меньше абсолютное значение тестовой статистики.

4. Изменились значения p . Обратите внимание, что значения p для каждой переменной также увеличились. Это связано с тем, что меньшие статистические данные теста связаны с большими значениями p.

Хотя значения p для наших коэффициентов изменились, переменная миль на галлон по-прежнему не является статистически значимой при α = 0,05, а вес переменной по-прежнему статистически значим при α = 0,05.