Как найти уравнение линейной регрессии по таблице
Часто вам может потребоваться найти уравнение линейной регрессии из таблицы данных.
Например, предположим, что вы получили следующую таблицу данных:
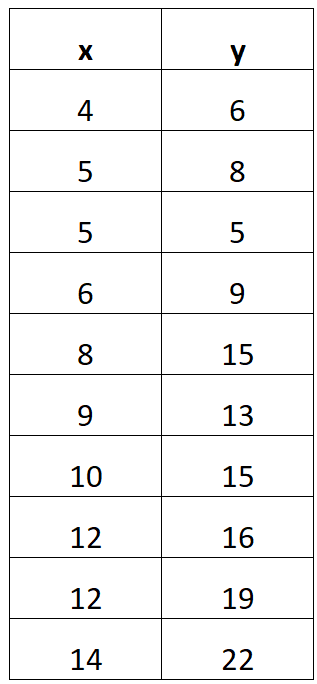
В следующем пошаговом примере показано, как найти уравнение линейной регрессии из этой таблицы данных.
Шаг 1: Рассчитайте X*Y, X 2 и Y 2
Сначала мы рассчитаем следующие показатели для каждой строки:
- х*у
- х2
- и 2
На следующем снимке экрана показано, как это сделать:
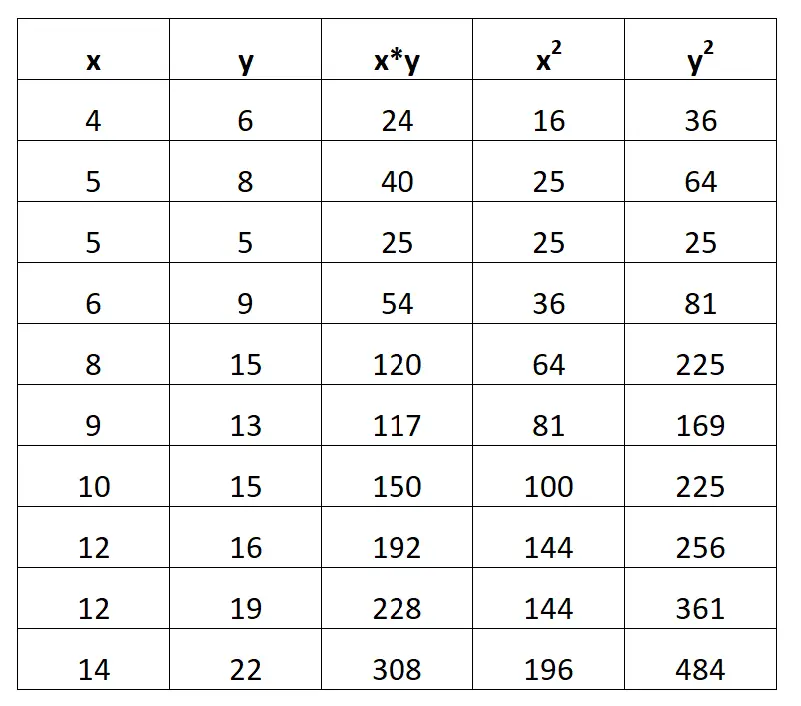
Шаг 2. Рассчитайте ΣX, ΣY, ΣX*Y, ΣX 2 и ΣY 2.
Далее посчитаем сумму каждого столбца:
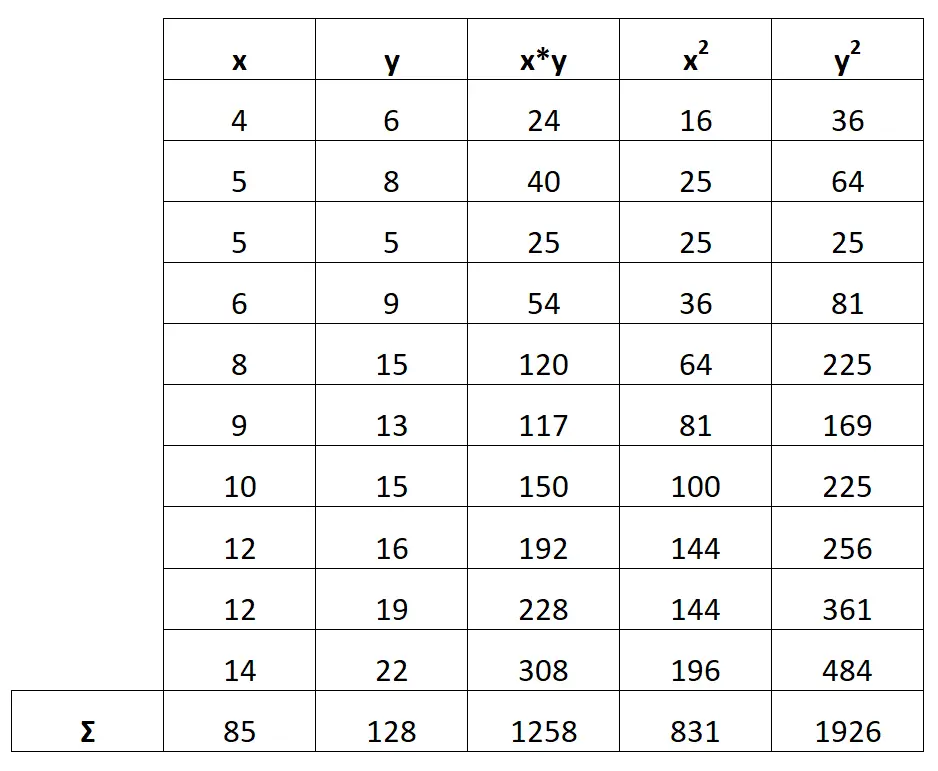
Шаг 3: Рассчитайте b 0
Формула для вычисления точки пересечения уравнения регрессии b 0 выглядит следующим образом:
- б 0 = ((Σy)(Σx 2 ) – (Σx)(Σxy)) / (n(Σx 2 ) – (Σx) 2 )
- б 0 = ((128)(831) – (85)(1258)) / (10(831) – (85) 2 )
- b0 = -0,518
Примечание . В формуле n представляет общее количество наблюдений. В этом примере всего было 10 наблюдений.
Шаг 4: Рассчитайте b 1
Формула для расчета наклона уравнения регрессии b 1 выглядит следующим образом:
- б 1 = (n(Σxy) – (Σx)(Σy)) / (n(Σx 2 ) – (Σx) 2 )
- б 1 = (10(1258) – (85)(128)) / (10(831) – (85) 2 )
- б1 = 1,5668
Шаг 5. Напишите уравнение линейной регрессии.
Окончательное уравнение линейной регрессии можно записать как:
- ŷ = б 0 + б 1 х
Таким образом, наше уравнение линейной регрессии будет записано следующим образом:
- ŷ = -0,518 + 1,5668x
Мы можем убедиться в правильности этого ответа, подставив значения из таблицы в простой калькулятор линейной регрессии :

Мы видим, что уравнение линейной регрессии из калькулятора соответствует тому, которое мы рассчитали вручную.
Дополнительные ресурсы
Следующие руководства предоставляют дополнительную информацию о линейной регрессии:
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Как интерпретировать коэффициенты регрессии