Наименее значимое отличие фишера: определение + пример

Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.

Допущения , используемые в ANOVA, следующие:

H ₀ : Средние значения равны для каждой группы.

_ХА : По крайней мере, один из способов отличается от других.

Если значение p ANOVA ниже определенного уровня значимости (например, α = 0,05), мы можем отвергнуть нулевую гипотезу и сделать вывод, что по крайней мере одно из групповых средних значений отличается от других.

Но чтобы точно знать, какие группы отличаются друг от друга, нам нужно провести апостериорный тест.

Обычно используемым апостериорным тестом является тест Фишера на основе наименее значимой разницы .

Чтобы выполнить этот тест, мы сначала вычисляем следующую статистику теста:

LSD = t _0,025 , _{DF w} * √ MS _W (1/n ₁ + 1/n ₁ )

Золото:

• t _.025 , _DFw : t-критическое значение таблицы распределения t с α = .025 и DF _w соответствует степеням свободы внутри групп таблицы ANOVA.
• MS _W : средние квадраты внутри групп в таблице ANOVA.
• n ₁ , n ₂ : размеры выборки каждой группы.

Затем мы можем сравнить среднюю разницу между каждой группой с этой тестовой статистикой. Если абсолютное значение средней разницы между двумя группами больше, чем тестовая статистика, мы можем заявить, что существует статистически значимая разница между групповыми средними.

В следующем примере показано, как на практике выполнить тест Фишера наименьшей значимой разницы.

Пример. Критерий наименьшей значимости Фишера

Предположим, профессор хочет знать, приводят ли три разных метода обучения к разным результатам тестов среди студентов. Чтобы проверить это, она случайным образом назначает 10 студентов использовать каждый метод обучения и записывает результаты их экзаменов.

В следующей таблице показаны результаты экзаменов каждого студента в зависимости от используемой методики обучения:

Профессор выполняет однофакторный дисперсионный анализ и получает следующие результаты:

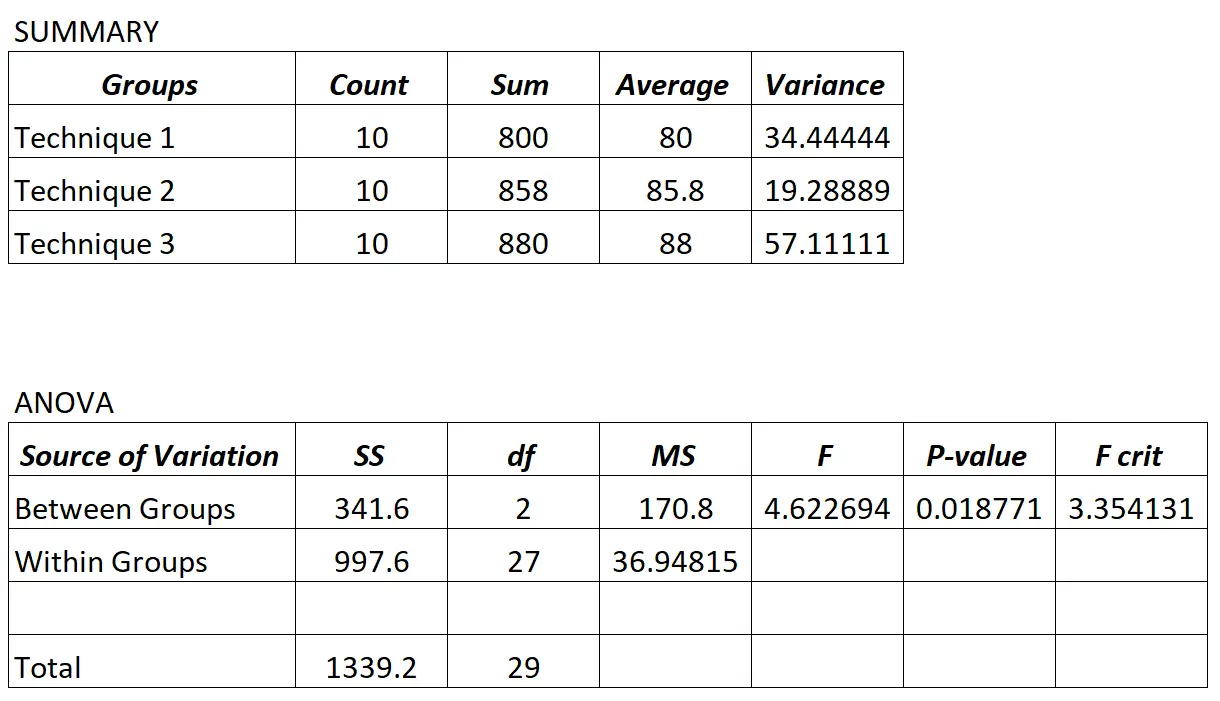
Поскольку значение p в таблице ANOVA (0,018771) меньше 0,05, мы можем заключить, что все средние баллы экзаменов между тремя группами не равны.

Итак, мы можем провести тест наименьшей значимой разницы Фишера, чтобы определить, какие групповые средние значения различаются.

Используя значения результата ANOVA, мы можем рассчитать статистику теста Фишера следующим образом:

• LSD = t _0,025 , _DFw * √ MS _W (1/n ₁ + 1/n ₁ )
• LSD = t _0,025 , ₂₇ * √ 36,948*(1/10 + 1/10)
• ЛСД = 2,052 * √ 7,3896
• ЛСД = 5,578

Затем мы можем рассчитать абсолютную среднюю разницу между каждой группой:

• Техника 1 против Техники 2: |80 – 85,8| = 5,8
• Техника 1 против Техники 3: |80 – 88| = 8
• Техника 2 против Техники 3: |85.8 – 88| = 2,2

Абсолютные средние различия между методом 1 и методом 2, а также между методом 1 и методом 3 превышают статистику критерия Фишера. Таким образом, мы можем заключить, что эти методы приводят к статистически значимо отличающимся средним баллам на экзаменах.

Мы также можем заключить, что нет существенной разницы в средних баллах на экзамене между методом 2 и методом 3.