Накопленная частота

В этой статье объясняется, что такое совокупная частота в статистике. Итак, вы узнаете значение кумулятивной частоты, как рассчитывается кумулятивная частота с примерами и, наконец, какие существуют типы кумулятивной частоты.

Что такое совокупная частота?

В статистике совокупная частота — это совокупная сумма частот. То есть совокупная частота значения равна частоте этого значения плюс частоты всех более низких значений.

Существует два типа совокупных частот: совокупная абсолютная частота и совокупная относительная частота. Ниже мы увидим, как рассчитывается каждый тип совокупной частоты.

Имейте в виду, что чтобы понять, что означает совокупная частота в статистике, вы должны сначала иметь четкое представление о понятии частоты. Вот почему рекомендуется посетить следующий пост, прежде чем продолжить объяснение:

Как рассчитать совокупную частоту

Шаги для расчета совокупной частоты статистической выборки:

1. Создайте таблицу со всеми различными значениями, которые встречаются в наборе данных, в порядке от наименьшего к наибольшему.
2. Найдите абсолютную частоту каждого значения.
3. Найдите совокупную частоту каждого значения, которая рассчитывается путем сложения частоты самого значения плюс частоты всех меньших значений.

Таким образом, формула расчета совокупной частоты выглядит следующим образом:

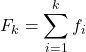
Золото:

• 

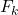
  — совокупная частота значения

  

  .

• 

  — абсолютная частота значения

  

  .

Обратите внимание, что эти шаги предназначены для расчета совокупной абсолютной частоты, но существует также совокупная относительная частота. Ниже мы увидим разницу между этими двумя типами накопленных частот и то, как находится каждый тип.

Виды накопительных частот

В статистике существует два типа совокупных частот :

• Кумулятивная абсолютная частота : это совокупная сумма абсолютных частот .
• Совокупная относительная частота : это совокупная сумма относительных частот .

Учитывая определение каждого типа накопленной частоты, ниже вы можете увидеть пример того, как каждый из них получается.

Совокупная абсолютная частота

Накопленная абсолютная частота обозначается символом F _i и рассчитывается путем сложения абсолютных частот значений, равных или меньших рассматриваемого значения. Далее у вас есть конкретный пример, в котором рассчитывается совокупная абсолютная частота набора статистических данных.

• Оценки, полученные по предмету «Статистика» в классе из 30 учащихся, следующие. Какова совокупная абсолютная частота каждой ноты?

Поскольку все числа могут быть только целыми числами, это дискретная переменная. Поэтому нет необходимости группировать данные по интервалам.

Итак, чтобы определить совокупную абсолютную частоту, мы должны сначала найти абсолютную частоту каждого значения, которая представляет собой количество раз, которое каждое значение появляется в статистической выборке.

Теперь, когда мы знаем абсолютную частоту каждого значения, мы можем вычислить их совокупную абсолютную частоту. Для этого у нас есть два варианта: либо мы добавляем абсолютную частоту значения плюс все абсолютные частоты наименьших значений, либо наоборот, мы добавляем абсолютную частоту значения плюс совокупную абсолютную частоту предыдущих значений. . ценить.

Вкратце, таблица с абсолютной совокупной частотой занятий выглядит следующим образом:

Обратите внимание, что накопленная абсолютная частота последнего значения всегда совпадает с общим количеством данных. В противном случае это означает, что вы ошиблись в расчете.

Совокупная относительная частота

Накопленная относительная частота обозначается символом H _i и рассчитывается путем сложения относительных частот значений, равных или меньших рассматриваемого значения. Ниже вы можете увидеть упражнение, решенное с теми же данными, что и предыдущая задача, в которой определяется кумулятивная относительная частота.

• Оценки, полученные по статистике в классе из 30 учеников, следующие. Какова совокупная относительная частота каждой ноты?

В данном случае переменная является дискретной, так как не может принимать десятичное значение. Таким образом, нет необходимости группировать данные по интервалам, а можно производить расчеты напрямую.

Итак, составляем таблицу частот и определяем абсолютную частоту каждого отдельного значения:

Далее вычисляем относительную частоту каждого значения, которая определяется путем деления абсолютной частоты на общее количество наблюдений (30).

И как только мы рассчитали абсолютную частоту и относительную частоту набора данных, мы можем получить совокупную относительную частоту. Для этого необходимо сложить относительную частоту рассматриваемого значения плюс все предыдущие относительные частоты или, что то же самое, предыдущую накопленную относительную частоту:

Короче говоря, таблица частот с абсолютной частотой, относительной частотой и совокупной относительной частотой выглядит следующим образом:

Имейте в виду, что последнее значение совокупной относительной частоты всегда должно быть равно 1. Если вы получили другое число, значит, вы допустили ошибку в расчетах.