Нормальное или равномерное распределение: в чем разница?

Нормальное распределение является наиболее часто используемым распределением вероятностей в статистике.

Он имеет следующие свойства:

• Симметричный
• Колоколообразный

Если мы создадим график нормального распределения, он будет выглядеть так:

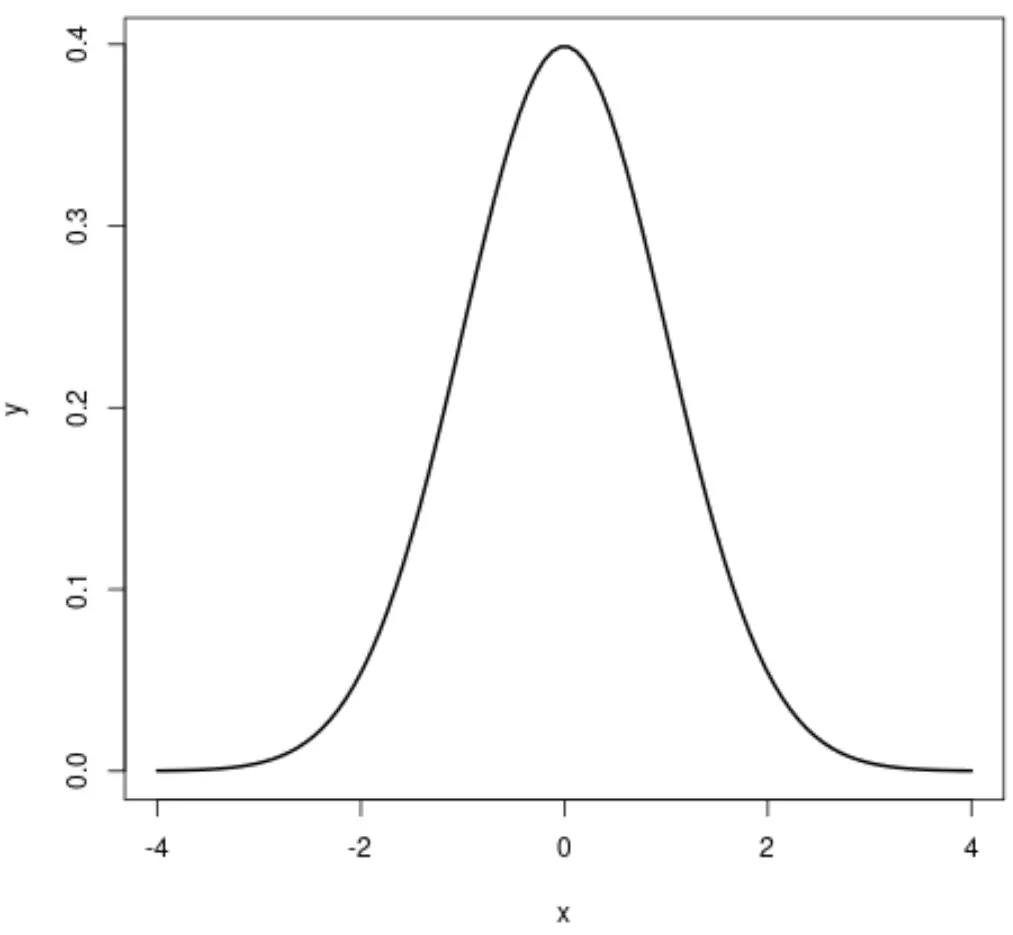
Равномерное распределение — это распределение вероятностей, в котором каждое значение между интервалом от a до b имеет одинаковую вероятность появления.

Он имеет следующие свойства:

• Симметричный
• Прямоугольной формы

Если мы создадим график равномерного распределения, он будет выглядеть так:

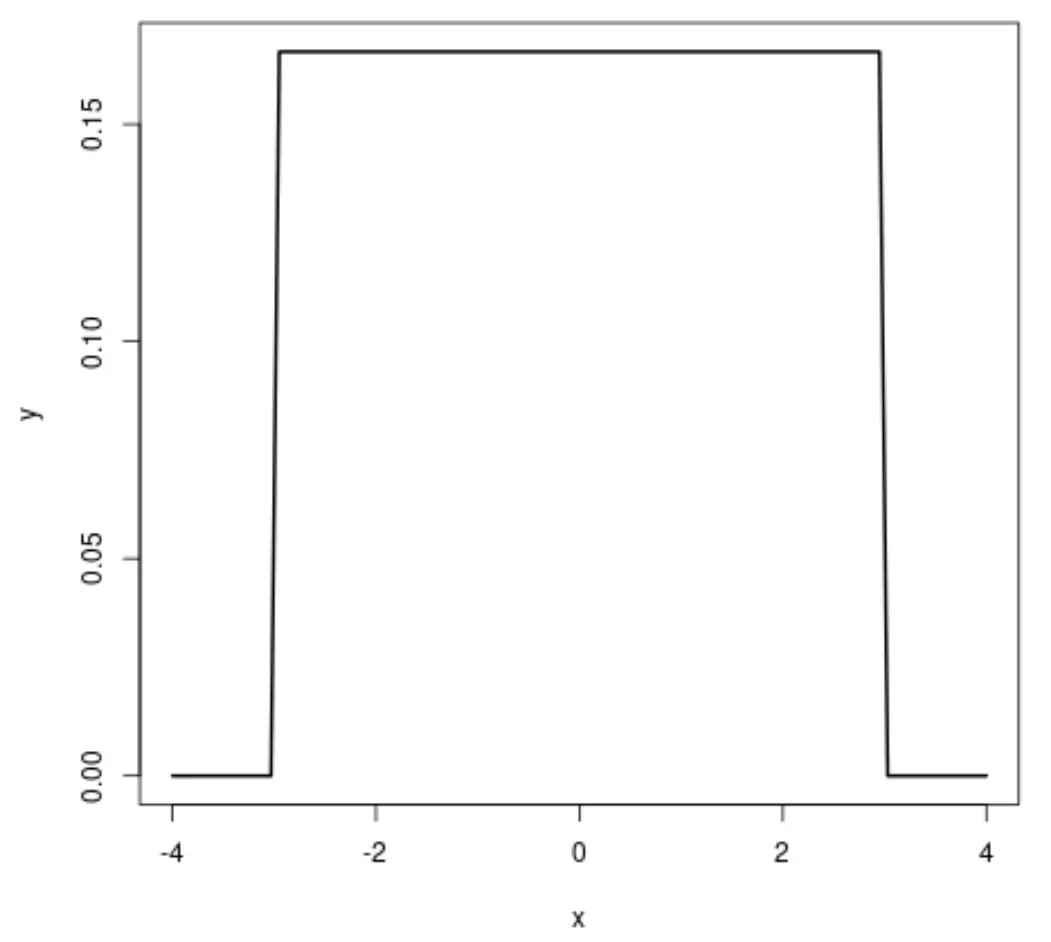
Нормальное распределение и равномерное распределение имеют следующее сходство :

• Оба распределения симметричны. То есть, если бы мы провели линию через центр распределения, левая и правая части распределения были бы идеально зеркальными:

Однако эти два дистрибутива имеют следующую разницу :

• Распределения имеют разную форму.
• Нормальное распределение имеет колоколообразную форму, что означает, что значения вблизи центра распределения встречаются с большей вероятностью, чем значения в хвостах распределения.
• Равномерное распределение имеет прямоугольную форму, что означает, что каждое значение в распределении имеет одинаковую вероятность появления.

Нормальное распределение или равномерное распределение: когда их использовать?

Нормальное распределение используется для моделирования явлений, которые имеют тенденцию следовать форме колоколообразной кривой. Например, хорошо известно, что вес новорожденных при рождении обычно составляет в среднем около 7,5 фунтов.

Гистограмма веса новорожденных в США имеет колоколообразную форму, что в целом соответствует нормальному распределению:

Большинство младенцев, вероятно, весят около 7,5 фунтов, некоторые весят менее 7 фунтов, а некоторые весят более 8 фунтов.

И наоборот, равномерное распределение используется для моделирования сценариев, в которых каждый потенциальный результат одинаково вероятен.

Классический пример — бросок кубика. Если вы бросите игральную кость один раз, вероятность того, что выпадет число от 1 до 6, будет равномерно распределена, поскольку каждое число имеет одинаковую вероятность выпадения.

Например, существует 6 возможных чисел, на которые может упасть кубик, поэтому вероятность того, что вы выпадете 1, равна 1/6.

Точно так же вероятность того, что вы выпадете 2, равна 1/6.

Аналогично, вероятность того, что у вас выпадет 3, равна 1/6.

И так далее.

Бонус: как построить график нормального и равномерного распределения.

Мы использовали следующий код в R для создания графиков нормального и равномерного распределений:

 #define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = " l ", lwd = 2 )

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))

Дополнительные ресурсы

6 конкретных примеров нормального распределения
5 конкретных примеров равномерного распределения
Симметричное распределение: определение + примеры