Нормальное распределение и t-распределение: в чем разница?

Нормальное распределение является наиболее часто используемым распределением во всей статистике и, как известно, является симметричным и колоколообразным.

Близкородственным распределением является распределение t , которое также является симметричным и колоколообразным, но имеет более тяжелые «хвосты», чем нормальное распределение.

Другими словами, больше значений в распределении расположено на концах, чем в центре по сравнению с нормальным распределением:

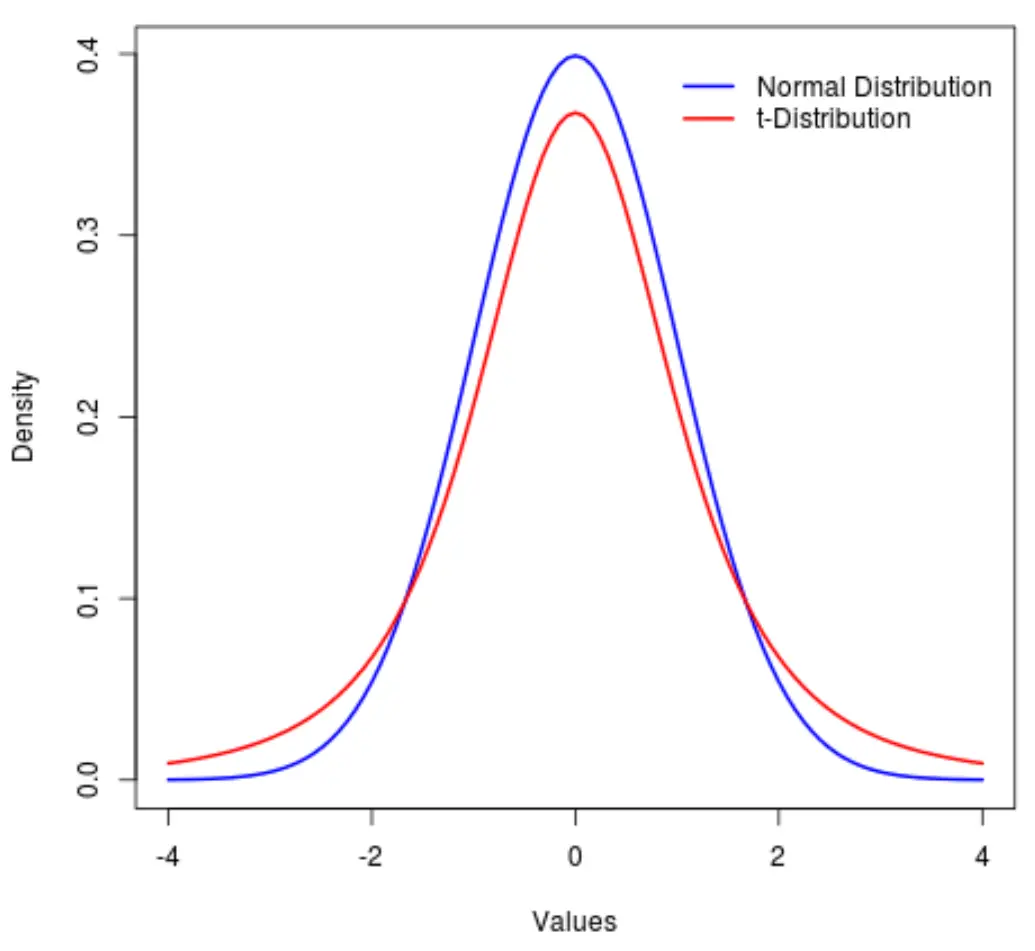
На статистическом жаргоне мы используем показатель, называемый эксцессом , чтобы измерить, насколько «тяжелым» является распределение. Итак, мы бы сказали, что эксцесс t-распределения больше, чем эксцесс нормального распределения.

На практике мы чаще всего используем t-распределение при проверке гипотез или построении доверительных интервалов .

Например, формула для расчета доверительного интервала для среднего значения совокупности:

Доверительный интервал = x +/- t _{1-α/2, n-1} *(s/√ n )

Золото:

• x : выборочное среднее
• t: критическое значение t, основанное на уровне значимости α и размере выборки n.
• s: выборочное стандартное отклонение
• n: размер выборки

В этой формуле мы используем критическое значение таблицы t вместо критического значения таблицы z, когда выполняется одно из следующих условий:

• Мы не знаем стандартное отклонение населения.
• Размер выборки меньше или равен 30.

Следующая блок-схема дает полезный способ узнать, следует ли вам использовать критическое значение из таблицы t или таблицы z:

Основное различие между использованием распределения t и использованием нормального распределения при построении доверительных интервалов заключается в том, что критические значения распределения t будут больше, что приведет к более широким доверительным интервалам.

Например, предположим, что мы хотим построить 95% доверительный интервал для среднего веса популяции черепах, чтобы собрать случайную выборку черепах со следующей информацией:

• Размер выборки n = 25
• Средний вес выборки x = 300
• Выборочное стандартное отклонение s = 18,5

Критическое значение z для уровня достоверности 95% составляет 1,96 , а критическое значение t для доверительного интервала 95% с df = 25-1 = 24 степенями свободы составляет 2,0639 .

Таким образом, 95% доверительный интервал для генерального среднего с использованием z-критического значения составляет:

95% ДИ = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]

В то время как 95% доверительный интервал для генеральной совокупности с использованием t-критического значения составляет:

95% ДИ = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]

Обратите внимание, что доверительный интервал с t-критическим значением шире.

Идея здесь заключается в том, что когда у нас небольшие размеры выборки, мы менее уверены в истинном среднем по совокупности, поэтому полезно использовать t-распределение для получения более широких доверительных интервалов, которые имеют больше шансов содержать истинное среднее по совокупности.

Визуализация степеней свободы распределения t

Следует отметить, что по мере увеличения степеней свободы t-распределение приближается к нормальному.

Чтобы проиллюстрировать это, рассмотрим следующий график, который показывает форму распределения t со следующими степенями свободы:

• дф = 3
• дф = 10
• дф = 30

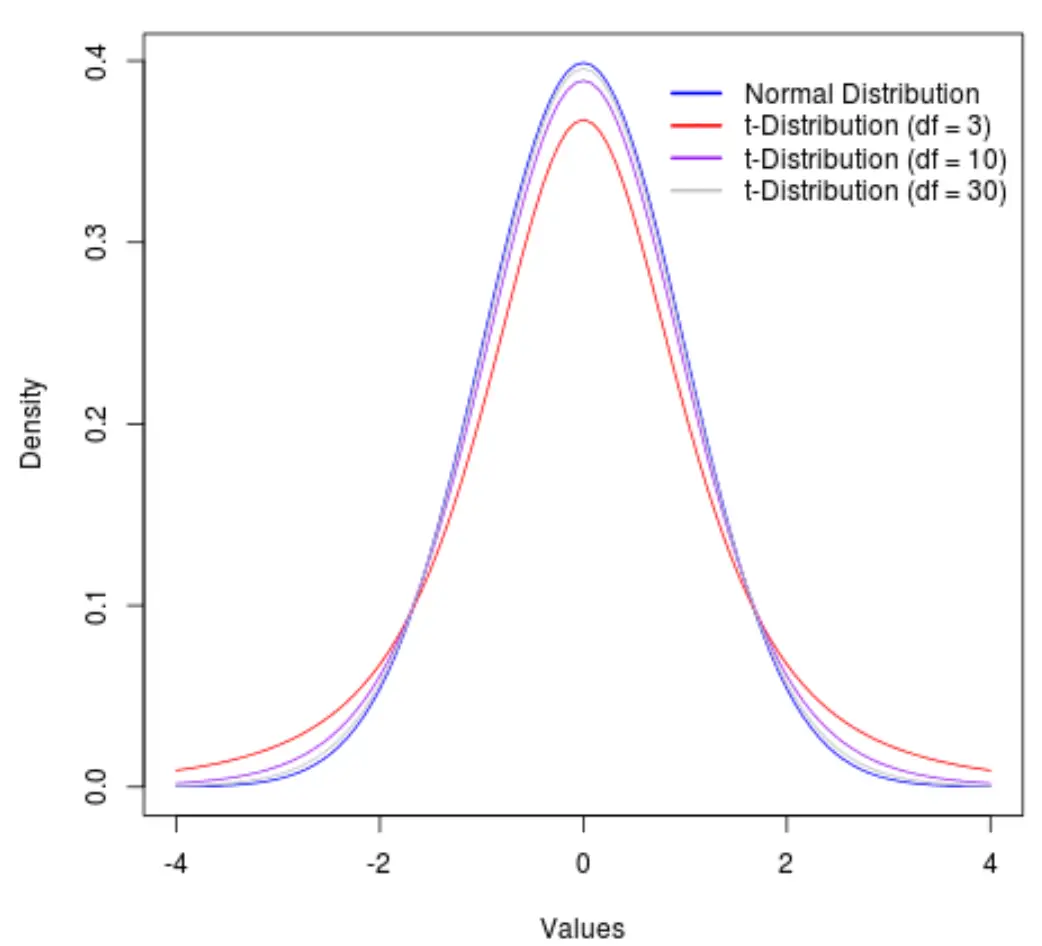
За пределами 30 степеней свободы распределение t и нормальное распределение становятся настолько похожими, что различия между использованием t-критического значения и z-критического значения в формулах становятся незначительными.