Нормальное распределение

Нормальное распределение является наиболее распространенным распределением вероятностей в статистике.

Нормальные распределения имеют следующие характеристики:

• Форма колокола
• Симметричный
• Среднее значение и медиана равны; оба расположены в центре распределения
• Около 68% данных находятся в пределах одного стандартного отклонения от среднего значения.
• Около 95% данных находятся в пределах двух стандартных отклонений от среднего значения.
• Около 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения.

Последние три пункта известны как эмпирическое правило , иногда называемое правилом 68-95-99,7 .

Связанный материал: Практическое правило (вопросы практики)

Как нарисовать нормальную кривую

Чтобы нарисовать нормальную кривую, нам нужно знать среднее значение и стандартное отклонение.

Пример 1: Предположим, что рост мужчин в определенной школе обычно распределяется со средним значением $\mu =\; 70\; дюймов\; и$ стандартным отклонением $\sigma \; =\; 2\; дюйма.\; Нарисуйте\; нормальную\; кривую.$

Шаг 1: Нарисуйте нормальную кривую.

Шаг 2: Среднее значение 70 дюймов находится посередине.

Шаг 3: Каждое стандартное отклонение соответствует расстоянию в 2 дюйма.

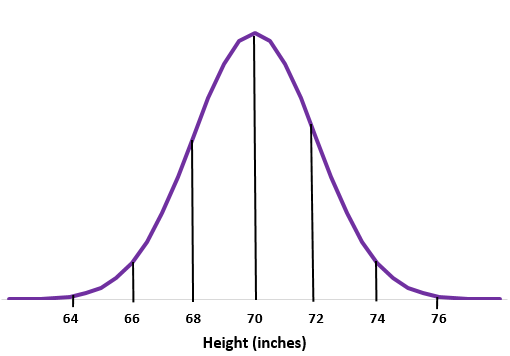
Пример 2: Предположим, что вес выдры определенного вида обычно распределяется со средним значением $\mu =\; 30\; фунтов\; и$ стандартным отклонением $\sigma \; =\; 5\; фунтов.\; Нарисуйте\; нормальную\; кривую.$

Шаг 1: Нарисуйте нормальную кривую.

Шаг 2: Средний вес в 30 фунтов находится посередине.

Шаг 3: Каждое стандартное отклонение соответствует расстоянию в 5 фунтов.

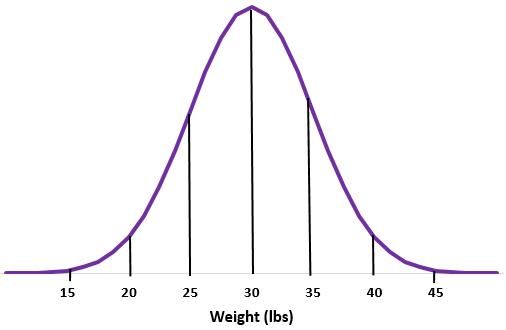
Как найти проценты, используя нормальное распределение

Эмпирическое правило , иногда называемое правилом 68-95-99,7 , гласит, что для нормально распределенной случайной величины 68% данных попадают в диапазон одного стандартного отклонения от среднего значения, 95% попадают в диапазон двух стандартных отклонений. отклонения от среднего значения, а 99,7% находятся в пределах трех стандартных отклонений от среднего значения.

Используя это правило, мы можем ответить на вопросы о процентах.

Пример: предположим, что рост мужчин в определенной школе обычно распределяется со средним значением $\mu =\; 70\; дюймов\; и$ стандартным отклонением $\sigma \; =\; 2\; дюйма.$

$Какой\; примерно\; процент\; мужчин\; в\; этой\; школе\; имеет\; рост\; более\; 74\; дюймов?$

Решение:

Шаг 1: Нарисуйте нормальное распределение со средним значением $\mu =\; 70\; дюймов\; и$ стандартным отклонением $\sigma \; =\; 2\; дюйма.$

Шаг 2. Рост 74 дюйма на два стандартных отклонения выше среднего. Добавьте проценты выше этой точки в нормальное распределение.

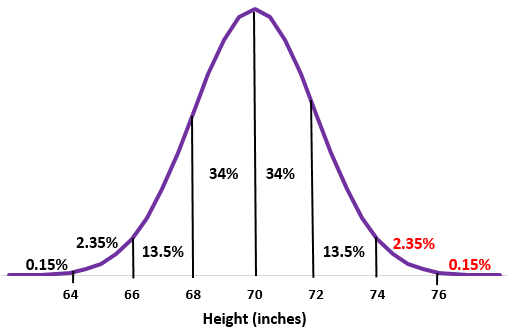
2,35% + 0,15% = 2,5%

Около 2,5% мужчин в этой школе имеют рост более 74 дюймов.

$Какой\; примерно\; процент\; мужчин\; в\; этой\; школе\; имеет\; рост\; от\; 68\; до\; 72\; дюймов?$

Решение:

Шаг 1: Нарисуйте нормальное распределение со средним значением $\mu =\; 70\; дюймов\; и$ стандартным отклонением $\sigma \; =\; 2\; дюйма.$

Шаг 2. Рост 68 дюймов и 72 дюйма на одно стандартное отклонение ниже и выше среднего соответственно. Просто сложите проценты между этими двумя точками нормального распределения.

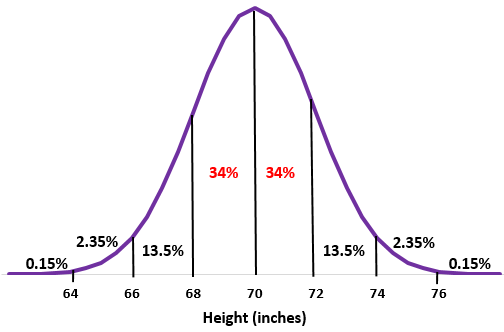
34% + 34% = 68%

Около 68% мужчин в этой школе имеют рост от 68 до 72 дюймов.

Как найти значения, используя нормальное распределение

Мы также можем использовать эмпирическое правило, чтобы ответить на вопросы о подсчете.

Пример: предположим, что вес определенного вида выдры обычно распределяется со средним значением $\mu =\; 30\; фунтов\; и$ стандартным отклонением $\sigma \; =\; 5\; фунтов.$

В одной колонии обитает 200 таких выдр. Сколько примерно этих выдр весят более 35 фунтов?

Решение:

Шаг 1: Нарисуйте нормальное распределение со средним значением $\mu =\; 30\; фунтов\; и$ стандартным отклонением $\sigma \; =\; 5\; фунтов.$

Шаг 2: Вес 35 фунтов на одно стандартное отклонение превышает среднее значение. Добавьте проценты выше этой точки в нормальное распределение.

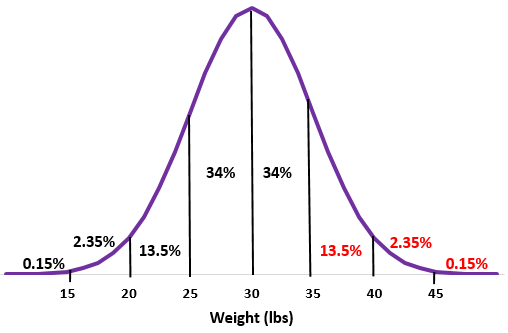
13,5% + 2,35% + 0,15% = 16%

Шаг 3: Поскольку в колонии 200 выдр, 16% от 200 = 0,16 * 200 = 32.

Около 32 выдр в этой колонии весят более 35 фунтов.

Сколько примерно выдр в этой колонии весят менее 30 фунтов?

Вместо того, чтобы следовать всем шагам, которые мы только что предприняли выше, мы можем признать, что медиана нормального распределения равна среднему значению, которое в данном случае составляет 30 фунтов.

Это означает, что половина выдр весит более 30 фунтов, а другая половина — менее 30 фунтов. Это означает, что 50% из 200 выдр весят менее 30 фунтов, поэтому 0,5 * 200 = 100 выдр .

Дополнительные ресурсы

Следующие руководства предоставляют дополнительную информацию о нормальном распределении:

6 конкретных примеров нормального распределения
Нормальное распределение и t-распределение: разница
Как создать колоколообразную кривую в Excel
Как создать колоколообразную кривую в Python