Стандартное нормальное распределение

В этой статье объясняется, что такое стандартное нормальное распределение и для чего оно используется. Также вы найдете свойства стандартного нормального распределения, таблицу с его характеристическими значениями и, кроме того, решенное упражнение.

Что такое стандартное нормальное распределение?

Стандартное нормальное распределение , также называемое единичным нормальным распределением , является простейшим случаем нормального распределения. Точнее, стандартное нормальное распределение — это нормальное распределение со значениями среднего и стандартного отклонения, равными 0 и 1 соответственно.

Следовательно, стандартное нормальное распределение определяется как N(0,1), где первый параметр — это среднее значение распределения, а второй параметр — его стандартное отклонение (или SD).

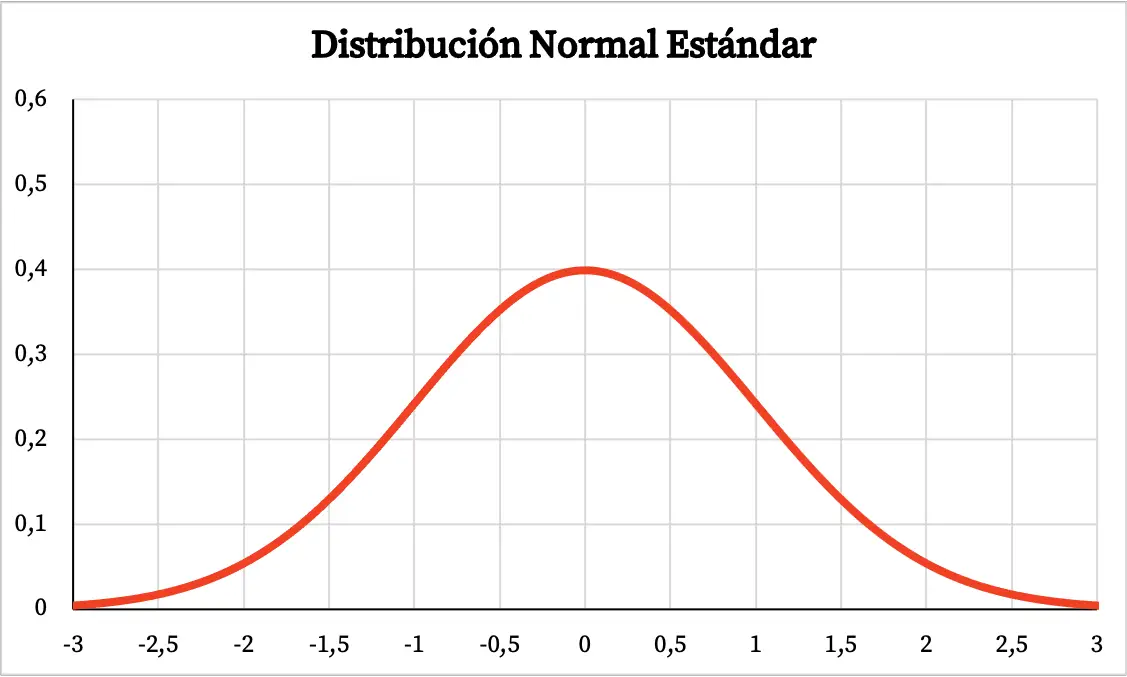
Таким образом, график стандартного нормального распределения выглядит следующим образом:

Формула стандартного нормального распределения

Чтобы преобразовать любое нормальное распределение в стандартное нормальное распределение, необходимо вычесть среднее значение нормального распределения из всех его значений, а затем разделить на стандартное отклонение нормального распределения.

Таким образом , формула стандартного нормального распределения выглядит следующим образом:

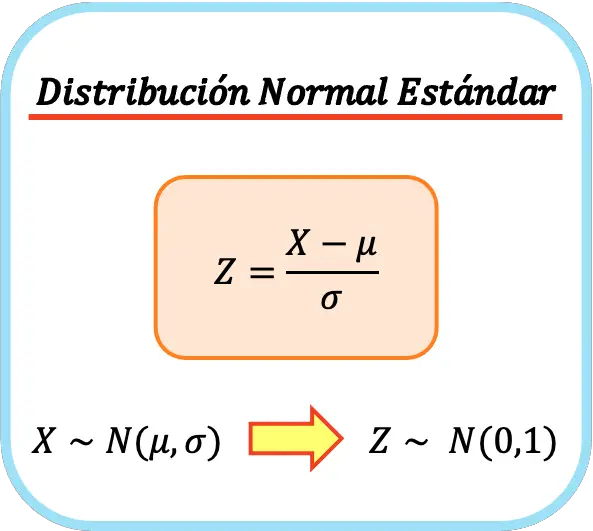
Таким образом, среднее арифметическое и стандартное отклонение новой переменной будут равны 0 и 1 соответственно, поэтому мы получим стандартное нормальное распределение. Этот процесс также называется одномерной нормализацией или одномерной нормализацией .

Стандартная таблица нормального распределения

Таблица стандартного нормального распределения — это таблица, содержащая вероятности того, что наблюдаемое значение меньше заданного значения стандартного нормального распределения.

Кроме того, поскольку функция нормального распределения зависит от его среднего значения и стандартного отклонения, таблица стандартного нормального распределения также используется, в расширении, для определения вероятностей любого нормального распределения. Для этого нормальное распределение набирается в стандартное нормальное распределение и затем смотрим в таблице, какая вероятность ему соответствует.

Итак, значения в стандартной таблице нормального распределения следующие:

Пример стандартного нормального распределения

Теперь, когда мы знаем определение стандартного нормального распределения и его формулу, ниже приведен конкретный пример, позволяющий хорошо понять эту концепцию.

• Непрерывная случайная величина подчиняется нормальному распределению со средним значением 45 и стандартным отклонением 15. Какова вероятность получить значение меньше или равное 58?

Чтобы найти вероятность нормального распределения, нам нужно использовать его таблицу признаков, но для этого нам сначала нужно выполнить процесс типизации, чтобы получить стандартное нормальное распределение. Поэтому мы используем стандартную формулу нормального распределения:

Поэтому мы вычитаем среднее значение из значения вероятности, а затем делим на стандартное отклонение.

После того как мы стандартизировали переменную, мы переходим к стандартной таблице вероятностей нормального распределения (см. выше), чтобы увидеть, какой вероятности соответствует значение 0,87:

Таким образом, вероятность получения значения, равного или меньшего 58, составляет 80,78%.

Характеристики стандартного нормального распределения

Стандартное нормальное распределение имеет следующие характеристики:

• Стандартное нормальное распределение — это симметричное распределение с центром в 0.
• Как и нормальное распределение, график стандартного нормального распределения имеет колоколообразную форму, при этом большая часть площади графика располагается около среднего значения.
• Следовательно, среднее значение, мода и медиана нормального распределения имеют одинаковое значение, равное 0.
• Стандартное нормальное распределение имеет максимум при z=0.
• Аналогично, стандартное нормальное распределение имеет две точки перегиба: z=-1 и z=+1.
• Согласно эмпирическому правилу, мы знаем, что 68% значений попадают в стандартное нормальное распределение между +1 и -1, 95% значений между +2 и -2 и 99,7% значений между + 3 и — 3.