Как выполнить регрессию ols в python (с примером)

Регрессия обычных наименьших квадратов (OLS) — это метод, который позволяет нам найти линию, которая лучше всего описывает взаимосвязь между одной или несколькими переменными-предикторами и переменной отклика .

Этот метод позволяет найти следующее уравнение:

ŷ = б ₀ + б ₁ х

Золото:

• ŷ : Предполагаемое значение ответа.
• b ₀ : Начало линии регрессии.
• b ₁ : Наклон линии регрессии.

Это уравнение может помочь нам понять взаимосвязь между предиктором и переменной ответа, а также его можно использовать для прогнозирования значения переменной ответа с учетом значения переменной-предиктора.

В следующем пошаговом примере показано, как выполнить регрессию OLS в Python.

Шаг 1. Создайте данные

В этом примере мы создадим набор данных, содержащий следующие две переменные для 15 студентов:

• Общее количество изученных часов
• Результаты экзамена

Мы выполним регрессию OLS, используя часы в качестве предикторной переменной и оценку на экзамене в качестве переменной ответа.

Следующий код показывает, как создать этот поддельный набор данных в пандах:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

Шаг 2. Выполните регрессию OLS

Далее мы можем использовать функции модуля statsmodels для выполнения регрессии OLS, используя часы в качестве предикторной переменной и оценку в качестве переменной ответа :

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

В столбце коэф мы можем увидеть коэффициенты регрессии и записать следующее подобранное уравнение регрессии:

Оценка = 65,334 + 1,9824*(часы)

Это означает, что каждый дополнительный час обучения связан с увеличением среднего балла на экзамене на 1,9824 балла.

Исходное значение 65 334 указывает нам средний ожидаемый результат экзамена для студента, обучающегося ноль часов.

Мы также можем использовать это уравнение, чтобы найти ожидаемый результат экзамена на основе количества часов обучения студента.

Например, студент, который учится 10 часов, должен набрать на экзамене балл 85,158 :

Оценка = 65,334 + 1,9824*(10) = 85,158

Вот как интерпретировать остальную часть описания модели:

• P(>|t|): это значение p, связанное с коэффициентами модели. Поскольку значение p для часов (0,000) меньше 0,05, мы можем сказать, что существует статистически значимая связь между часами и баллами .
• R-квадрат: Это говорит нам о том, что процент вариации результатов экзамена можно объяснить количеством изученных часов. В этом случае 83,1% разницы в баллах можно объяснить учебными часами.
• F-статистика и значение p: F-статистика ( 63,91 ) и соответствующее значение p ( 2,25e-06 ) говорят нам об общей значимости модели регрессии, т. е. полезны ли переменные-предикторы в модели для объяснения вариаций. в переменной ответа. Поскольку значение p в этом примере меньше 0,05, наша модель статистически значима, и часы считаются полезными для объяснения вариаций оценок .

Шаг 3. Визуализируйте наиболее подходящую линию

Наконец, мы можем использовать пакет визуализации данных matplotlib для визуализации линии регрессии, соответствующей фактическим точкам данных:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

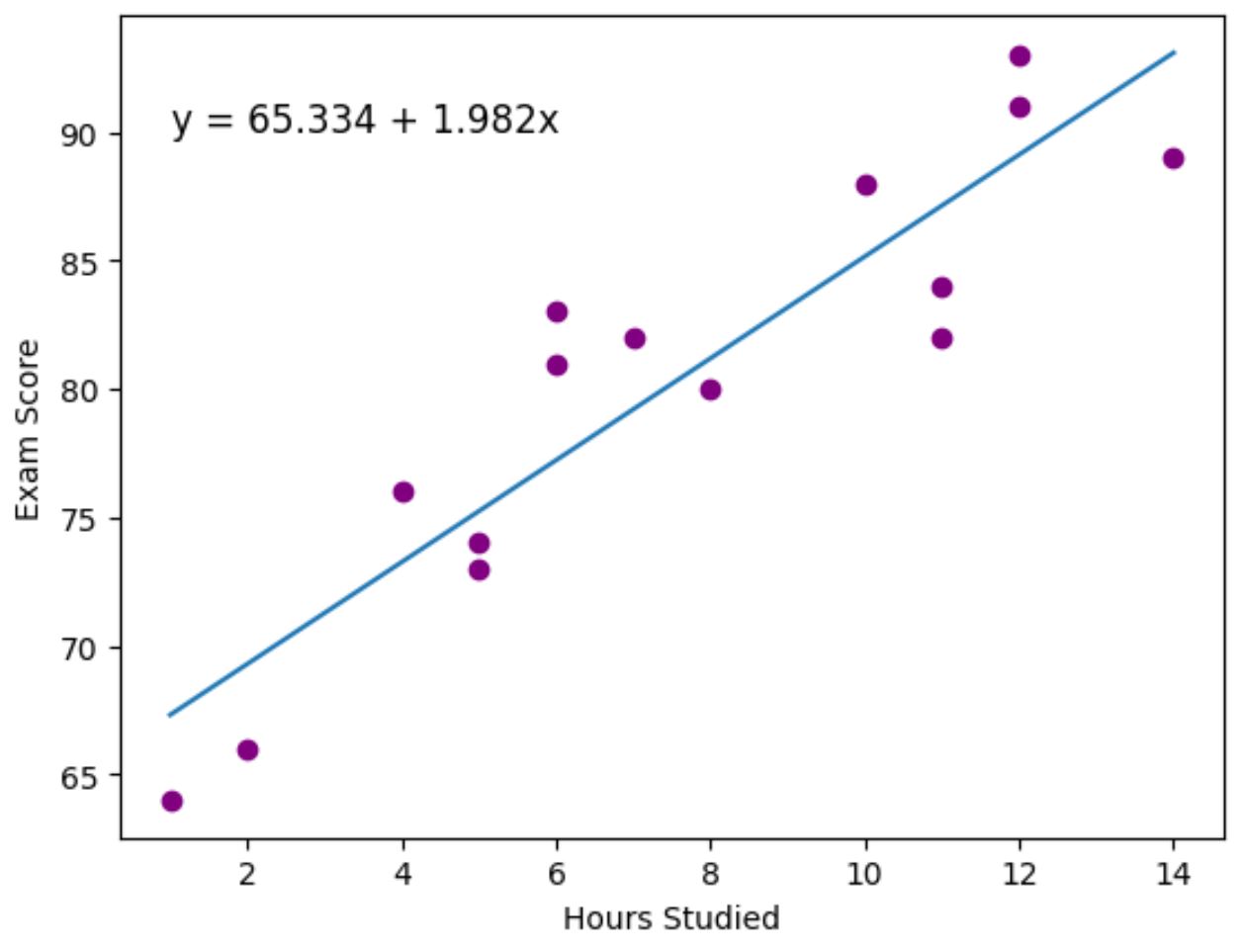
Фиолетовые точки представляют фактические точки данных, а синяя линия представляет собой подобранную линию регрессии.

Мы также использовали функцию plt.text() , чтобы добавить подобранное уравнение регрессии в верхний левый угол графика.

Глядя на график, становится ясно, что подобранная линия регрессии довольно хорошо отражает взаимосвязь между переменной часов и переменной оценки .

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи на Python:

Как выполнить логистическую регрессию в Python
Как выполнить экспоненциальную регрессию в Python
Как рассчитать AIC регрессионных моделей в Python