Что такое остатки в статистике?

Остаток — это разница между наблюдаемым значением и прогнозируемым значением в регрессионном анализе .

Он рассчитывается следующим образом:

Остаток = Наблюдаемое значение – Прогнозируемое значение

Напомним, что целью линейной регрессии является количественная оценка взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика . Для этого линейная регрессия находит линию, которая лучше всего «соответствует» данным, называемую линией регрессии по методу наименьших квадратов .

Эта линия дает прогноз для каждого наблюдения в наборе данных, но маловероятно, что прогноз, сделанный линией регрессии, будет точно соответствовать наблюдаемому значению.

Разница между прогнозом и наблюдаемым значением является остатком. Если мы построим наблюдаемые значения и наложим подобранную линию регрессии, остатки для каждого наблюдения будут представлять собой расстояние по вертикали между наблюдением и линией регрессии:

Наблюдение имеет положительный остаток , если его значение превышает прогнозируемое значение, полученное с помощью линии регрессии.

И наоборот, наблюдение имеет отрицательный остаток, если его значение меньше прогнозируемого значения, полученного с помощью линии регрессии.

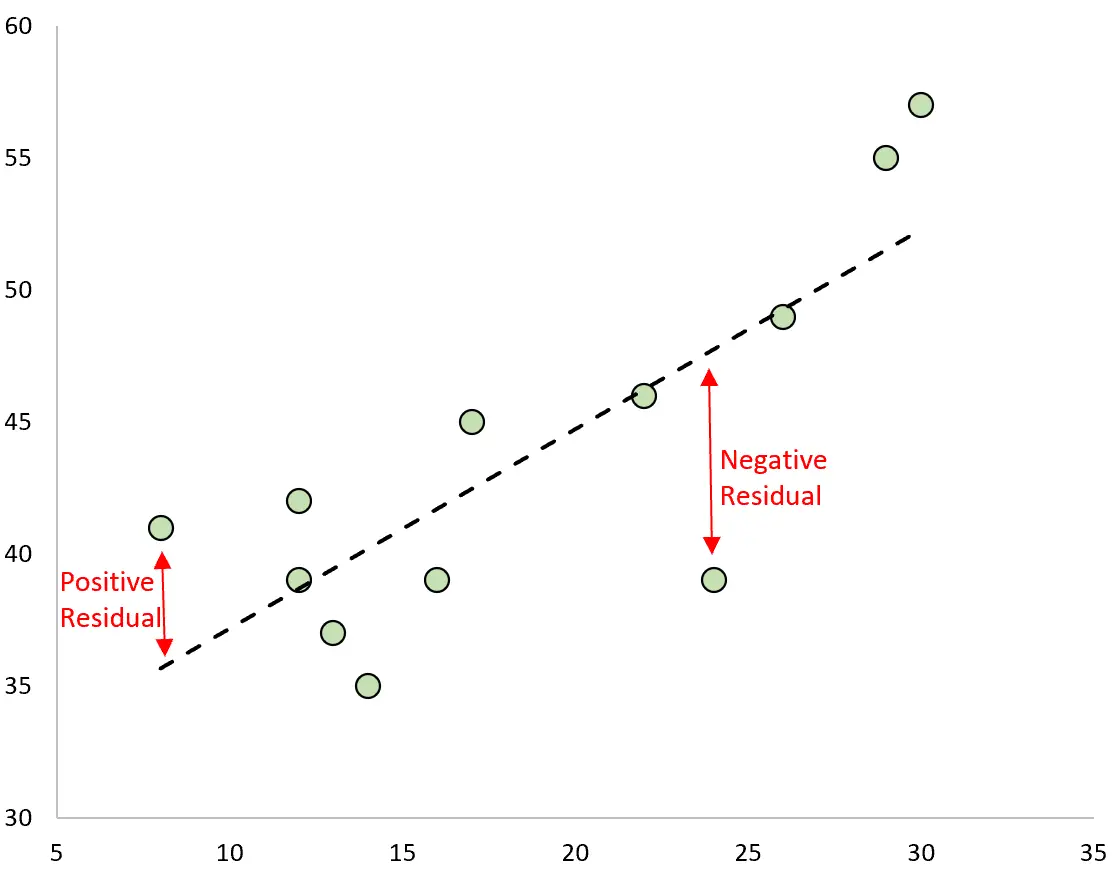
Некоторые наблюдения будут иметь положительные остатки, тогда как другие будут иметь отрицательные остатки, но сумма всех остатков будет равна нулю .

Пример расчета остатков

Предположим, у нас есть следующий набор данных с 12 наблюдениями:

Если мы используем статистическое программное обеспечение (например, R , Excel , Python , Stata и т. д.), чтобы подогнать линию линейной регрессии к этому набору данных, мы обнаружим, что наиболее подходящей линией окажется:

у = 29,63 + 0,7553x

Используя эту строку, мы можем вычислить прогнозируемое значение для каждого значения Y на основе значения X. Например, прогнозируемое значение первого наблюдения будет:

у = 29,63 + 0,7553*(8) = 35,67

Затем мы можем вычислить невязку для этого наблюдения следующим образом:

Остаток = Наблюдаемое значение – Прогнозируемое значение = 41 – 35,67 = 5,33

Мы можем повторить этот процесс, чтобы найти остаток для каждого наблюдения:

Если мы создадим диаграмму рассеяния для визуализации наблюдений с помощью подобранной линии регрессии, мы увидим, что некоторые наблюдения лежат выше линии, а другие — ниже линии:

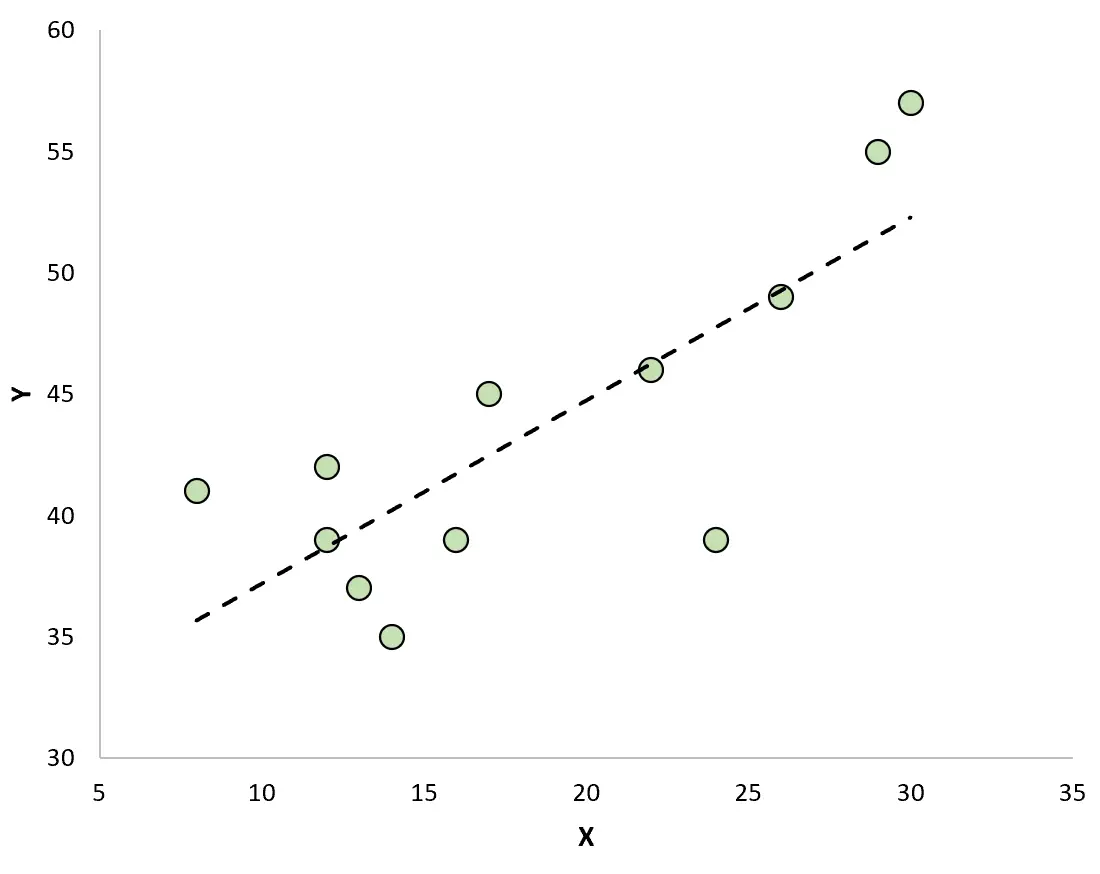
Свойства остатков

Остатки обладают следующими свойствами:

• Каждое наблюдение в наборе данных имеет соответствующий остаток. Таким образом, если набор данных содержит в общей сложности 100 наблюдений, модель выдаст 100 прогнозируемых значений, что в итоге даст 100 остатков.
• Сумма всех остатков равна нулю.
• Среднее значение остатков равно нулю.

Как остатки используются на практике?

На практике остатки используются в регрессии по трем различным причинам:

1. Оценить адекватность модели.

После того, как мы построили подобранную линию регрессии, мы можем вычислить остаточную сумму квадратов (RSS) , которая представляет собой сумму всех квадратов остатков. Чем ниже RSS, тем лучше модель регрессии соответствует данным.

2. Проверьте предположение о нормальности.

Одним из ключевых предположений линейной регрессии является то, что остатки имеют нормальное распределение.

Чтобы проверить эту гипотезу, мы можем создать график QQ, который представляет собой тип графика, который мы можем использовать, чтобы определить, соответствуют ли остатки модели нормальному распределению.

Если точки на графике примерно образуют прямую диагональную линию, то предположение о нормальности выполнено.

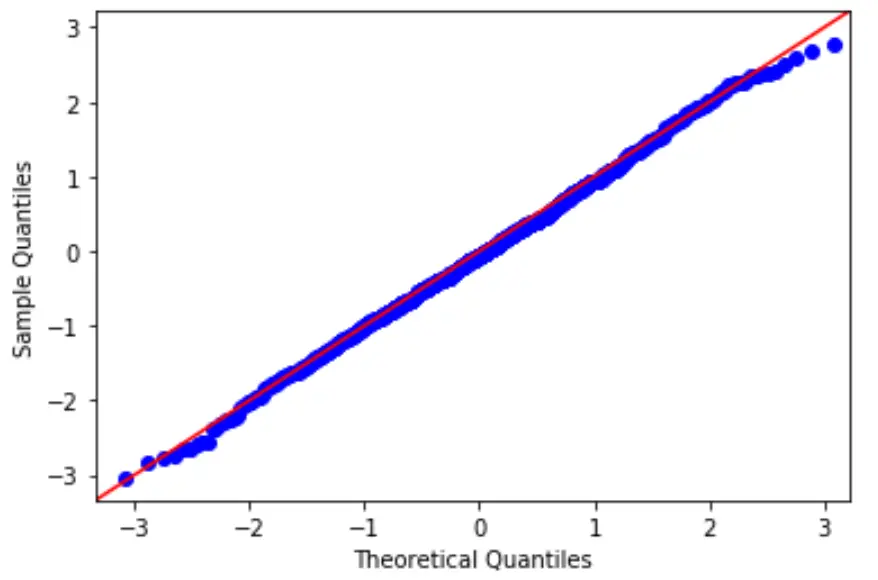
3. Проверьте предположение о гомоскедастичности.

Еще одно ключевое предположение линейной регрессии заключается в том, что остатки имеют постоянную дисперсию на каждом уровне x. Это называется гомоскедастичностью. Когда это не так, остатки страдают от гетероскедастичности .

Чтобы проверить, выполняется ли это предположение, мы можем создать график остатков , который представляет собой диаграмму рассеяния, показывающую остатки в сравнении с прогнозируемыми значениями модели.

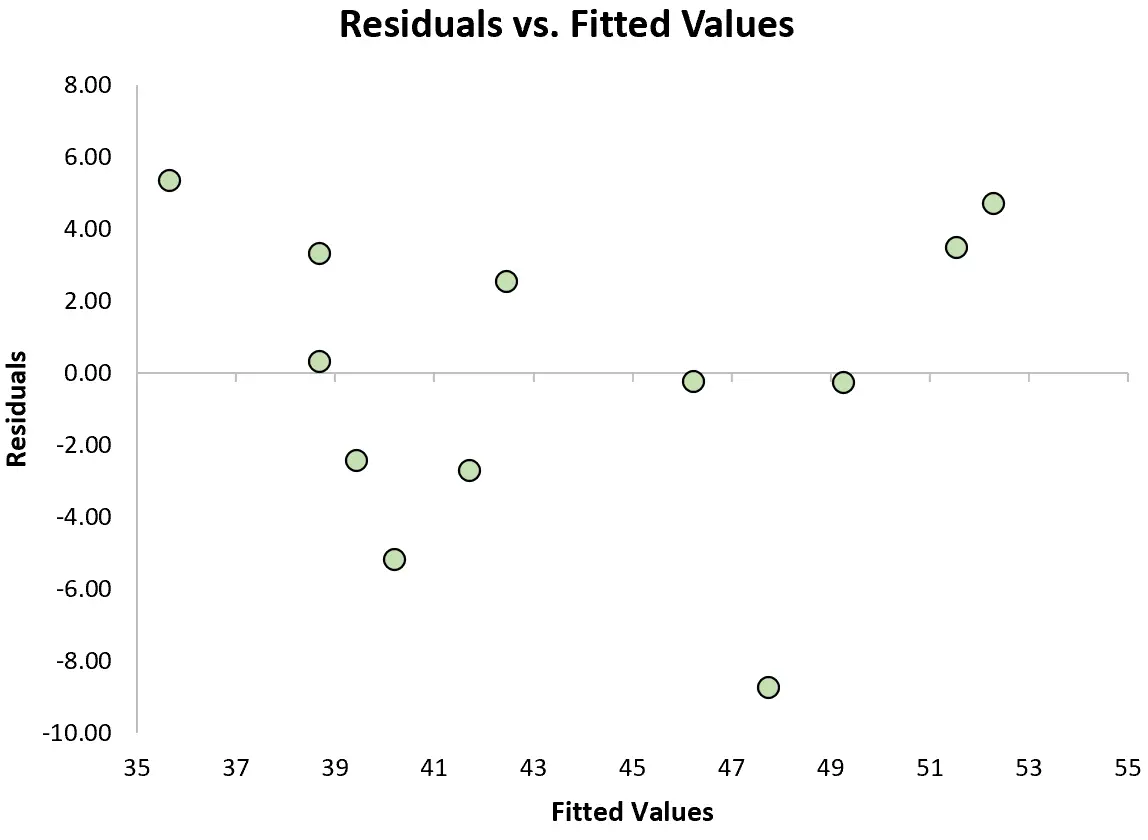
Если остатки примерно равномерно распределены вокруг нуля на графике без четкой тенденции, то мы обычно говорим, что предположение о гомоскедастичности выполнено.

Дополнительные ресурсы

Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Четыре предположения линейной регрессии
Как создать остаточный график в Excel