Относительная частота

В этой статье вы узнаете, что такое относительная частота в статистике, как получить относительную частоту и решить два пошаговых упражнения на относительную частоту.

Что такое относительная частота?

В статистике относительная частота — это мера, которая указывает, сколько раз значение появляется в выборке данных в пропорции или процентах. Точнее, относительная частота равна абсолютной частоте, деленной на общее количество данных.

Например, если абсолютная частота значения равна 15 и всего имеется 100 точек данных, относительная частота этого значения равна 0,15 (15/100 = 0,15).

Обычно символ h _i используется для обозначения относительной частоты. Хотя в статистическом сообществе до сих пор нет единого мнения, поэтому вы можете увидеть относительную частоту, представленную другим символом.

Как рассчитать относительную частоту

Относительная частота равна абсолютной частоте, деленной на общее количество данных. Поэтому, чтобы вычислить относительную частоту, необходимо сначала найти абсолютную частоту, а затем разделить ее на общее количество наблюдений.

Итак, формула относительной частоты выглядит следующим образом:

Золото:

• 

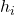
  это относительная частота.

• 

  это абсолютная частота.

• 

  общее количество данных.

С другой стороны, чтобы вычислить относительную частоту в процентах , то есть относительную частоту, выраженную в процентах, просто умножьте предыдущую формулу на 100:

Примеры относительной частоты

После того, как вы ознакомились с определением относительной частоты, ниже приведены два реальных примера, чтобы вы могли увидеть, как рассчитывается этот тип частоты. В первом примере определяется относительная частота дискретной переменной, а во втором примере — непрерывной переменной.

Пример 1: дискретная переменная

• Оценки, полученные по предмету «Статистика» в классе из 30 учащихся, следующие. Какова относительная частота каждой ноты?

Переменная в этом упражнении является дискретной, поскольку данные могут быть только целыми числами; поэтому нет необходимости группировать данные по интервалам.

Чтобы найти относительную частоту, мы должны сначала определить абсолютную частоту. Итак, мы создаем таблицу частот и вычисляем абсолютную частоту для каждого отдельного значения:

Теперь, когда мы рассчитали абсолютную частоту, мы можем вычислить относительную частоту. Для этого просто разделите каждую абсолютную частоту на общее количество данных (30):

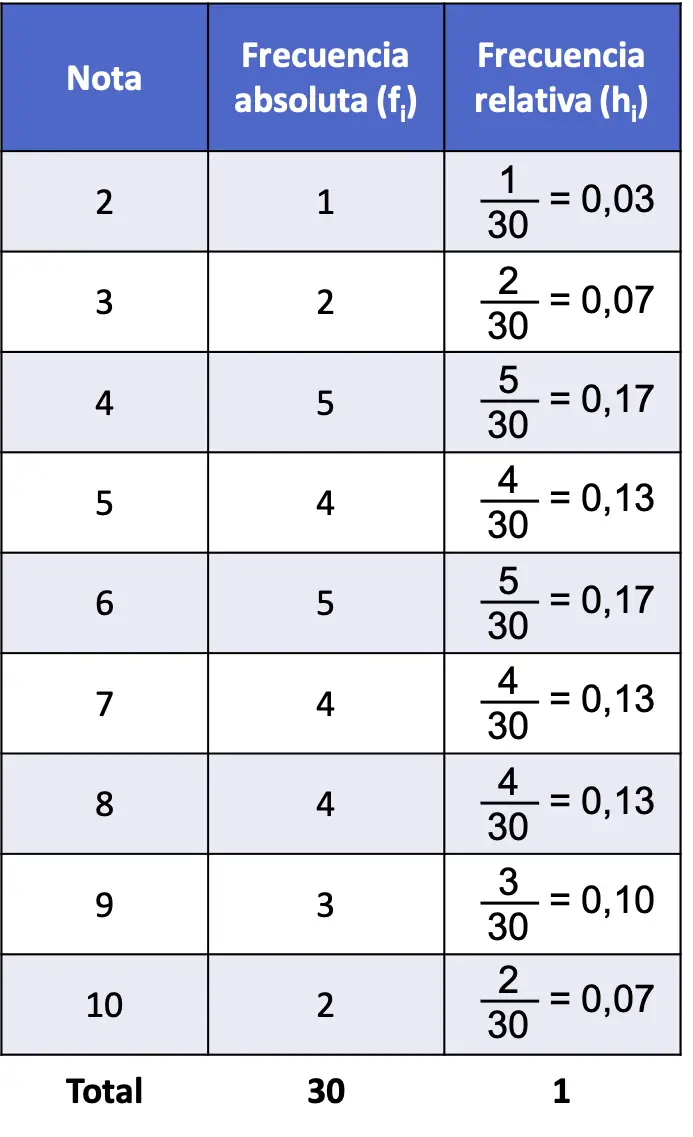
Итак, таблица частот задачи с абсолютной частотой и относительной частотой выглядит следующим образом:

Обратите внимание, что сумма всех относительных частот всегда дает 1, иначе это означает, что некоторые расчеты неверны.

Пример 2: непрерывная переменная

• Был измерен рост 20 человек и получены результаты, указанные ниже. Разделите данные на интервалы и найдите относительную частоту каждого интервала.

Данные в этой статистической выборке принадлежат непрерывной переменной, поскольку они десятичные и, следовательно, переменная может принимать любое значение. Поэтому, прежде чем проводить частотные расчеты, мы сначала сгруппируем данные в интервалы с амплитудой в 10 десятых.

Далее составляем таблицу частот с абсолютной частотой каждого интервала:

И как только мы найдем абсолютную частоту, мы сможем получить относительную частоту каждого интервала, разделив его абсолютную частоту на общее количество данных (20):

Совокупная относительная частота

Как следует из названия, кумулятивная относительная частота — это еще один тип частоты, используемый в статистике и рассчитываемый на основе относительной частоты.

Точнее, совокупная относительная частота значения равна сумме относительной частоты самого значения плюс относительные частоты всех меньших значений.

Чтобы вы могли увидеть, как получается совокупная относительная частота, совокупная относительная частота набора данных в первом примере была рассчитана ниже: