Введение в полиномиальную регрессию

Когда у нас есть набор данных с переменной-предиктором и переменной отклика , мы часто используем простую линейную регрессию для количественной оценки связи между двумя переменными.

Однако простая линейная регрессия (SLR) предполагает, что связь между предиктором и переменной ответа является линейной. Записанный в математической записи, SLR предполагает, что соотношение принимает форму:

Y = β ₀ + β ₁ X + ε

Но на практике связь между двумя переменными на самом деле может быть нелинейной, и попытка использовать линейную регрессию может привести к плохо подходящей модели.

Одним из способов учета нелинейной связи между предиктором и переменной отклика является использование полиномиальной регрессии , которая принимает форму:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

В этом уравнении h называется степенью многочлена.

Когда мы увеличиваем значение h , модель способна лучше учитывать нелинейные зависимости, но на практике мы редко выбираем значение h больше 3 или 4. За пределами этой точки модель становится слишком гибкой и не соответствует данным .

Технические примечания

• Хотя полиномиальная регрессия может соответствовать нелинейным данным, она по-прежнему считается формой линейной регрессии, поскольку она линейна по коэффициентам _β1 , _β2 ,…, _βh .
• Полиномиальную регрессию также можно использовать для нескольких переменных-предикторов, но это создает условия взаимодействия в модели, что может сделать модель чрезвычайно сложной, если используется несколько переменных-предикторов.

Когда использовать полиномиальную регрессию

Мы используем полиномиальную регрессию, когда связь между предиктором и переменной ответа является нелинейной.

Существует три распространенных способа обнаружения нелинейной зависимости:

1. Создайте диаграмму рассеяния.

Самый простой способ обнаружить нелинейную зависимость — создать диаграмму рассеяния переменной отклика и переменной-предиктора.

Например, если мы создадим следующую диаграмму рассеяния, мы увидим, что связь между двумя переменными приблизительно линейна, поэтому простая линейная регрессия, вероятно, будет хорошо работать с этими данными.

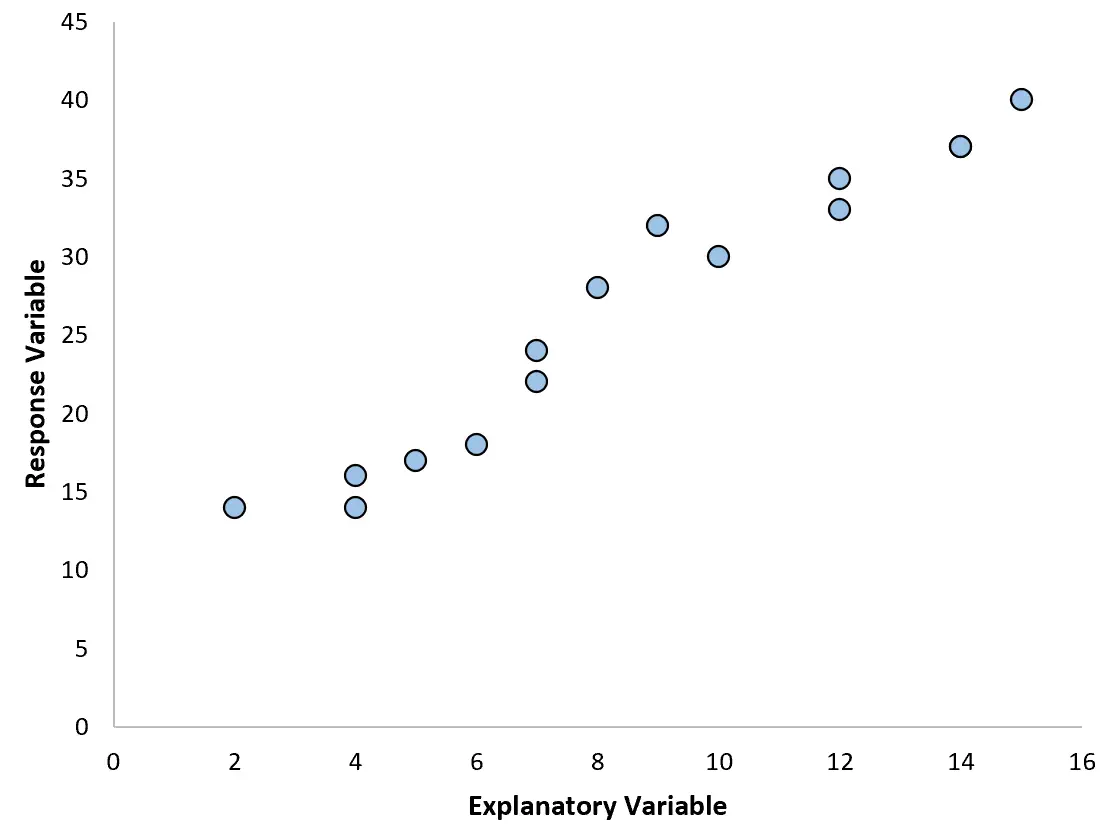
Однако если наша диаграмма рассеяния выглядит как один из следующих графиков, мы можем увидеть, что связь нелинейная, и поэтому хорошей идеей будет полиномиальная регрессия:

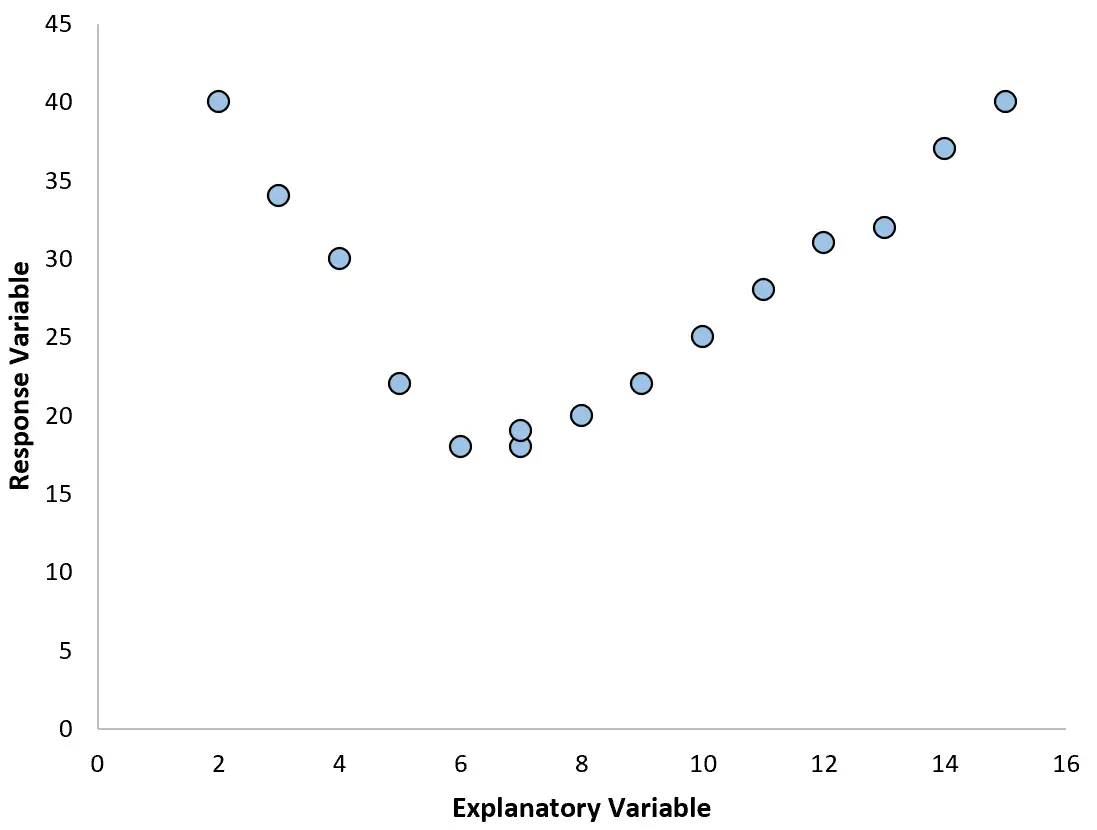
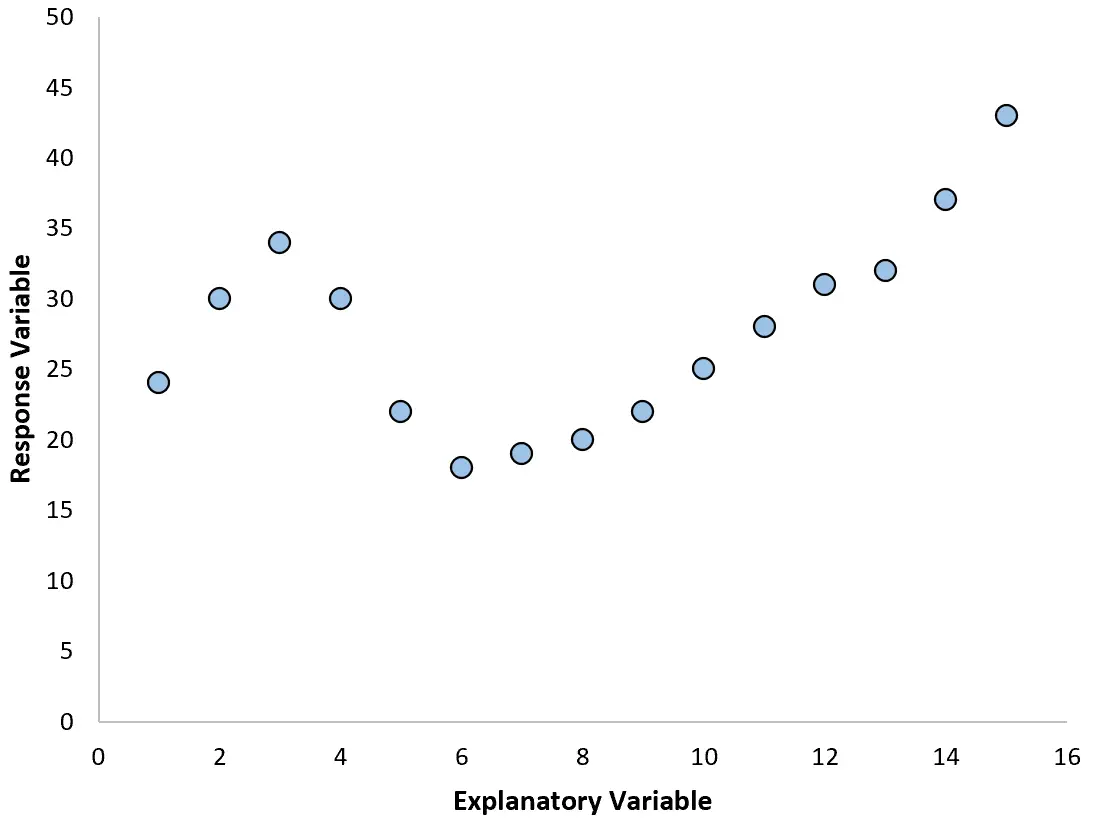
2. Создайте график остатков на основе подобранного графика.

Другой способ обнаружить нелинейность — подогнать к данным простую модель линейной регрессии, а затем построить график остатков в зависимости от подобранных значений .

Если остатки на графике распределены примерно равномерно около нуля без четкой тенденции, то, вероятно, будет достаточно простой линейной регрессии.

Однако, если остатки показывают на графике нелинейную тенденцию, это указывает на то, что связь между предиктором и ответом, скорее всего, нелинейна.

3. Рассчитайте R ² модели.

Значение R ² регрессионной модели показывает процент вариации переменной отклика, который можно объяснить предикторной переменной(ями).

Если вы подгоняете простую модель линейной регрессии к набору данных, а значение R ² модели довольно низкое, это может указывать на то, что связь между предиктором и переменной отклика более сложная, чем простая линейная зависимость.

Это может быть признаком того, что вам, возможно, придется вместо этого попробовать полиномиальную регрессию.

Связанный: Что такое хорошее значение R-квадрата?

Как выбрать степень многочлена

Модель полиномиальной регрессии принимает следующую форму:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

В этом уравнении h — степень многочлена.

Но как выбрать значение h ?

На практике мы подбираем несколько разных моделей с разными значениями h и выполняем k-кратную перекрестную проверку , чтобы определить, какая модель дает наименьшую среднеквадратичную ошибку (MSE).

Например, мы можем подогнать следующие модели к данному набору данных:

• Y = β ₀ + β ₁
• Y = β ₀ + β ₁ X + β ₂ X ²
• ^{Y =} _β0 + _β1X + _β2X2 + _β3X3
• Y = β ₀ + β ₁ X + β ₂ X ² + β ₃ X ³ + β ₄ X ⁴

Затем мы можем использовать k-кратную перекрестную проверку для расчета теста MSE для каждой модели, который покажет нам, насколько хорошо каждая модель работает с данными, которые она никогда раньше не видела.

Компромисс смещения и дисперсии полиномиальной регрессии

При использовании полиномиальной регрессии существует компромисс между смещением и дисперсией . Когда мы увеличиваем степень полинома, смещение уменьшается (поскольку модель становится более гибкой), но дисперсия увеличивается.

Как и во всех моделях машинного обучения, нам необходимо найти оптимальный компромисс между предвзятостью и дисперсией.

В большинстве случаев это позволяет в некоторой степени увеличить степень полинома, но после определенного значения модель начинает адаптироваться к шуму в данных, и MSE теста начинает уменьшаться.

Чтобы гарантировать, что мы подходим к модели, которая является гибкой, но не слишком гибкой, мы используем перекрестную проверку в k-кратном размере, чтобы найти модель, которая дает наименьший тест MSE.

Как выполнить полиномиальную регрессию

В следующих руководствах представлены примеры выполнения полиномиальной регрессии в различных программах:

Как выполнить полиномиальную регрессию в Excel
Как выполнить полиномиальную регрессию в R
Как выполнить полиномиальную регрессию в Python