Полиномиальная регрессия в google таблицах (шаг за шагом)
Регрессионный анализ используется для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
Наиболее распространенным типом регрессионного анализа является простая линейная регрессия , используемая, когда переменная-предиктор и переменная отклика имеют линейную связь.
Однако иногда связь между переменной-предиктором и переменной отклика является нелинейной.
В этих случаях имеет смысл использовать полиномиальную регрессию , которая может учитывать нелинейные связи между переменными.
В этом руководстве представлен пошаговый пример выполнения полиномиальной регрессии в Google Таблицах.
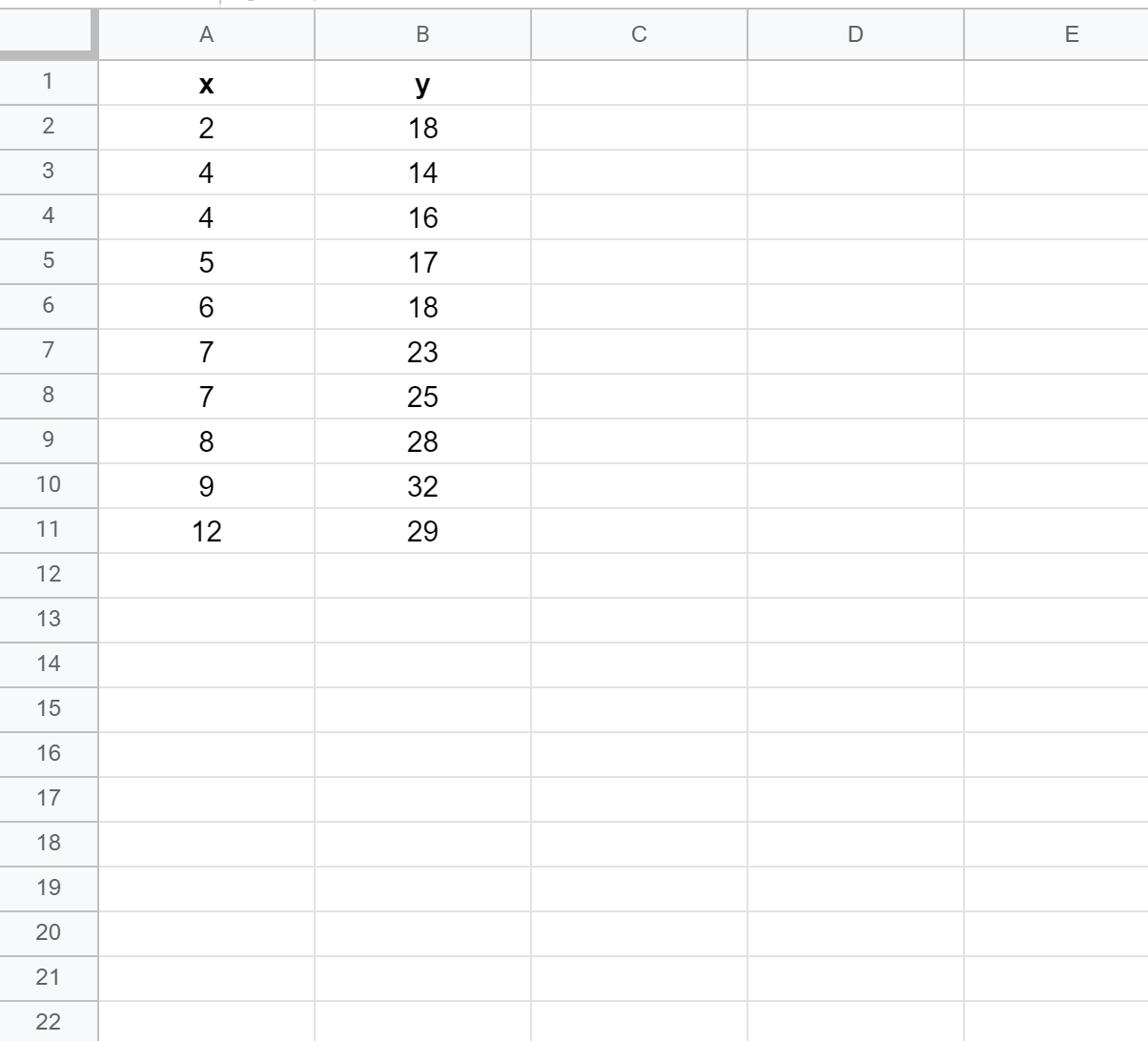
Шаг 1. Создайте данные
Сначала давайте создадим поддельный набор данных со следующими значениями:
Шаг 2. Создайте диаграмму рассеяния
Далее мы создадим диаграмму рассеяния для визуализации данных.
Сначала выделите ячейки A2:B11 следующим образом:
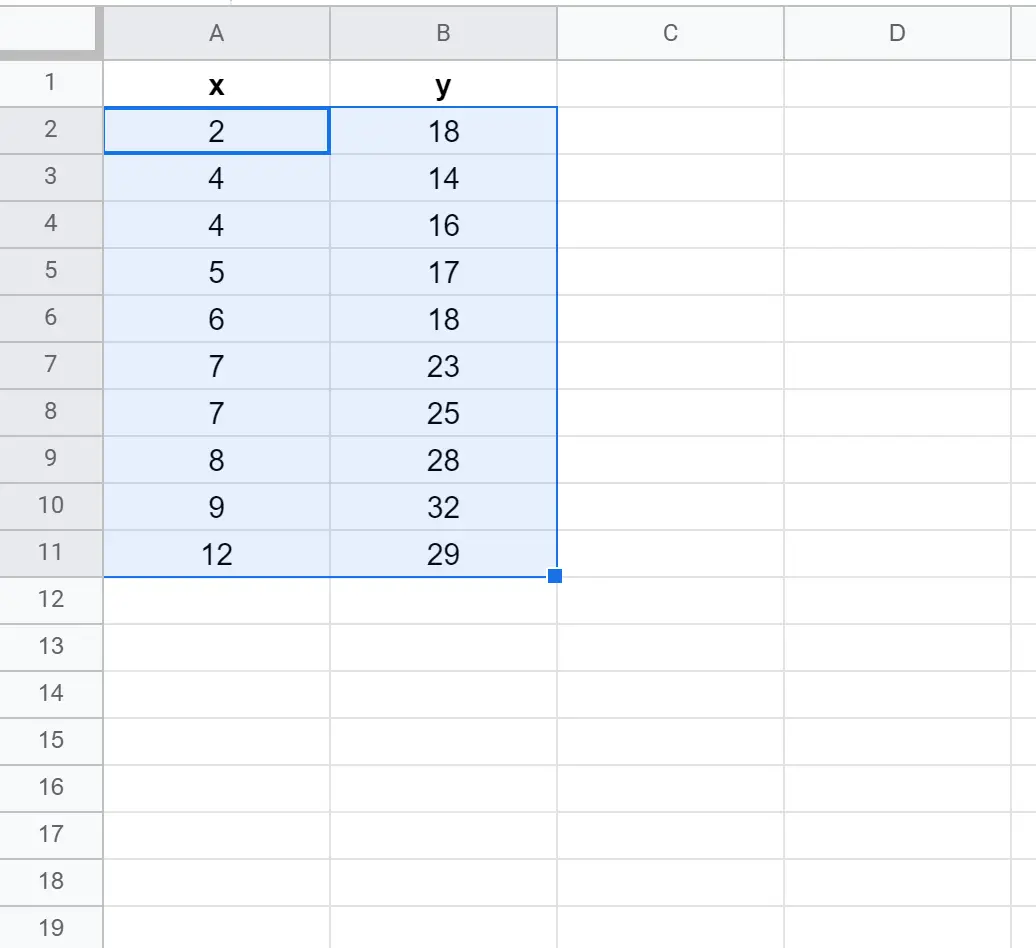
Затем перейдите на вкладку «Вставка» , затем нажмите «Диаграмма» в раскрывающемся меню:
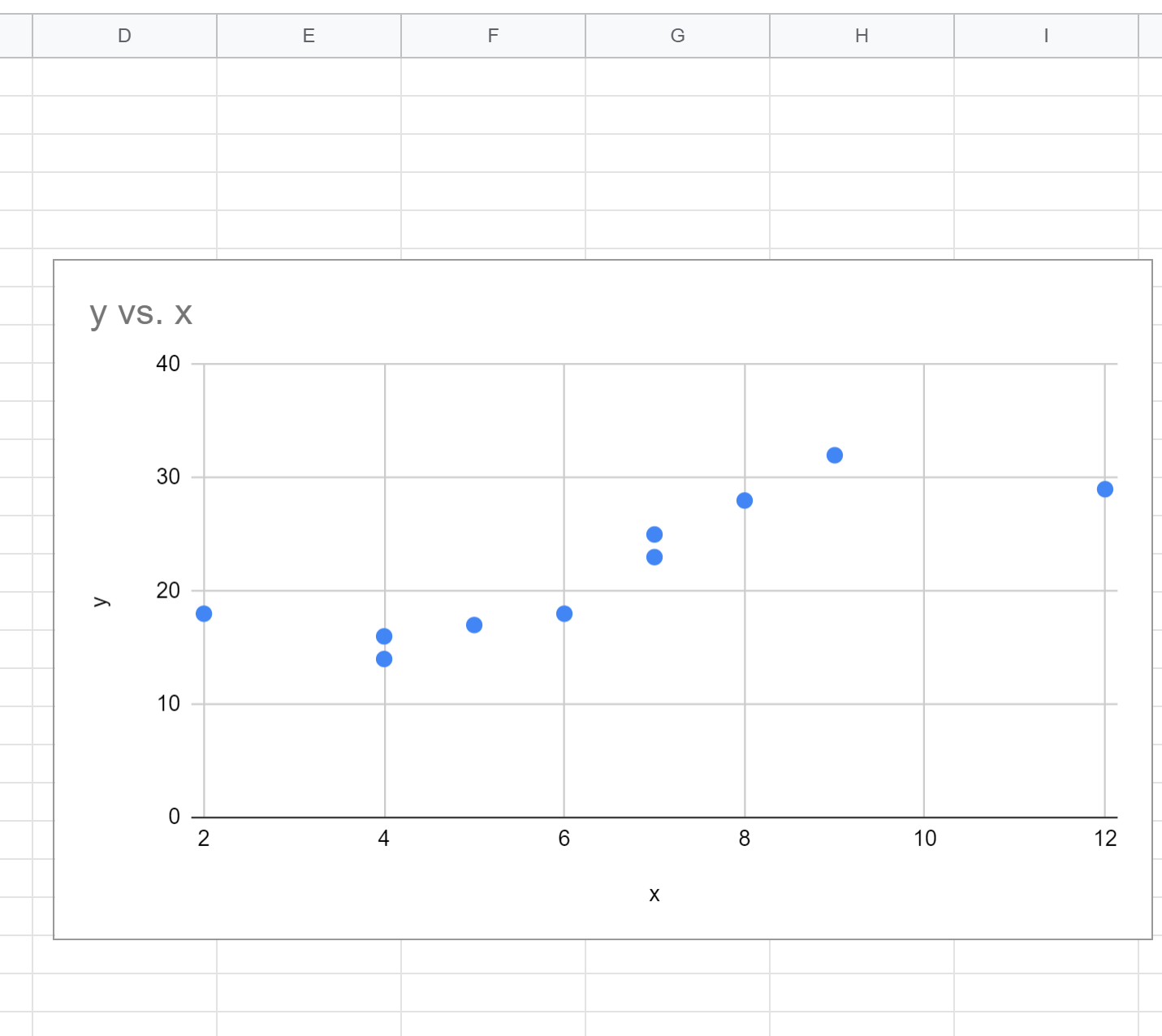
По умолчанию Google Sheets вставит диаграмму рассеяния:
Шаг 3. Найдите уравнение полиномиальной регрессии
Затем дважды щелкните в любом месте диаграммы рассеяния, чтобы отобразить окно редактора графиков справа:
Далее нажмите «Серия» . Затем прокрутите вниз и установите флажок рядом с «Линия тренда» и измените тип на «Полиномиальный» . В разделе «Метка» выберите «Использовать уравнение» , затем установите флажок «Показать R2» .
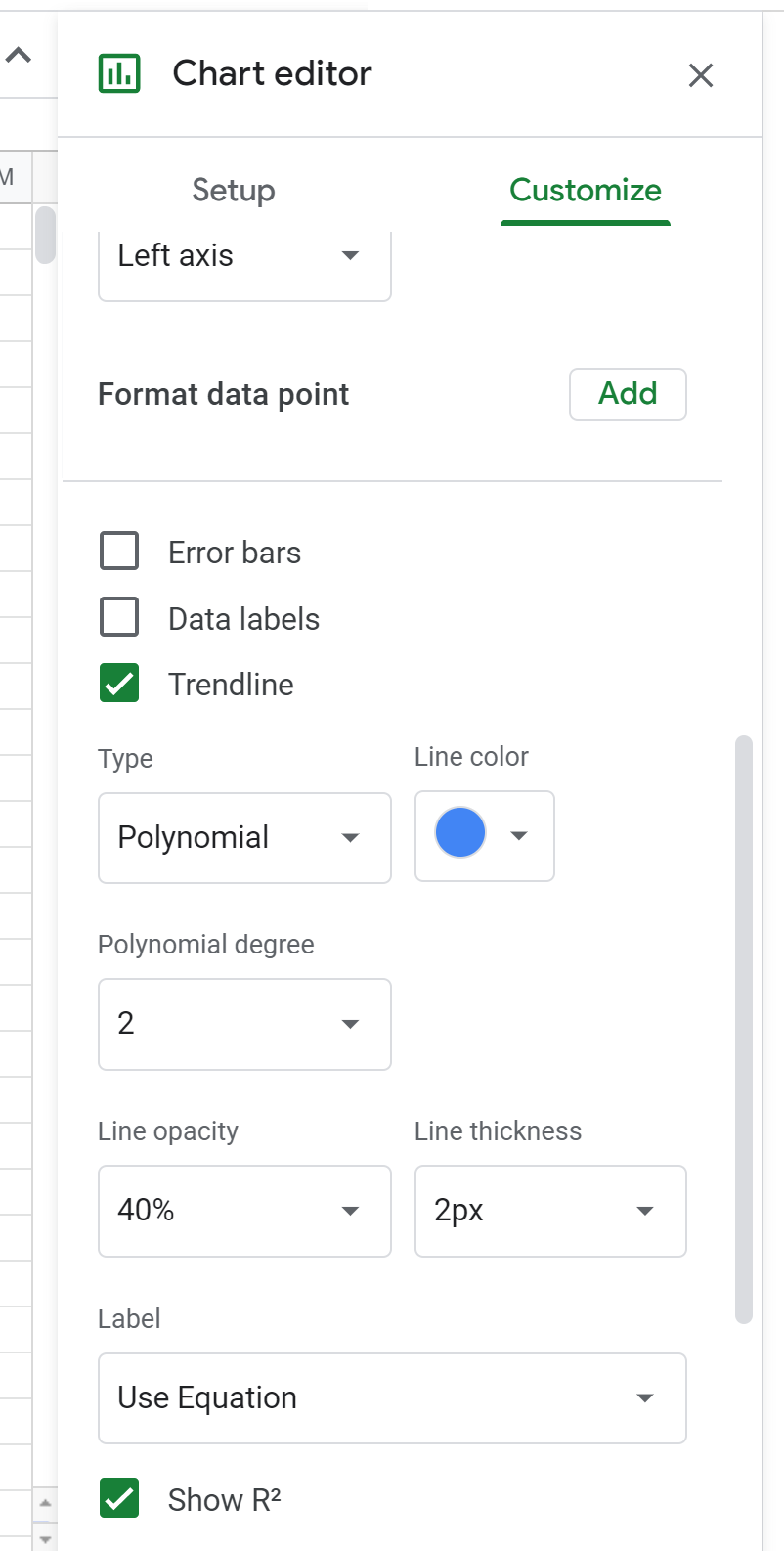
Это приведет к появлению следующей формулы над диаграммой рассеяния:
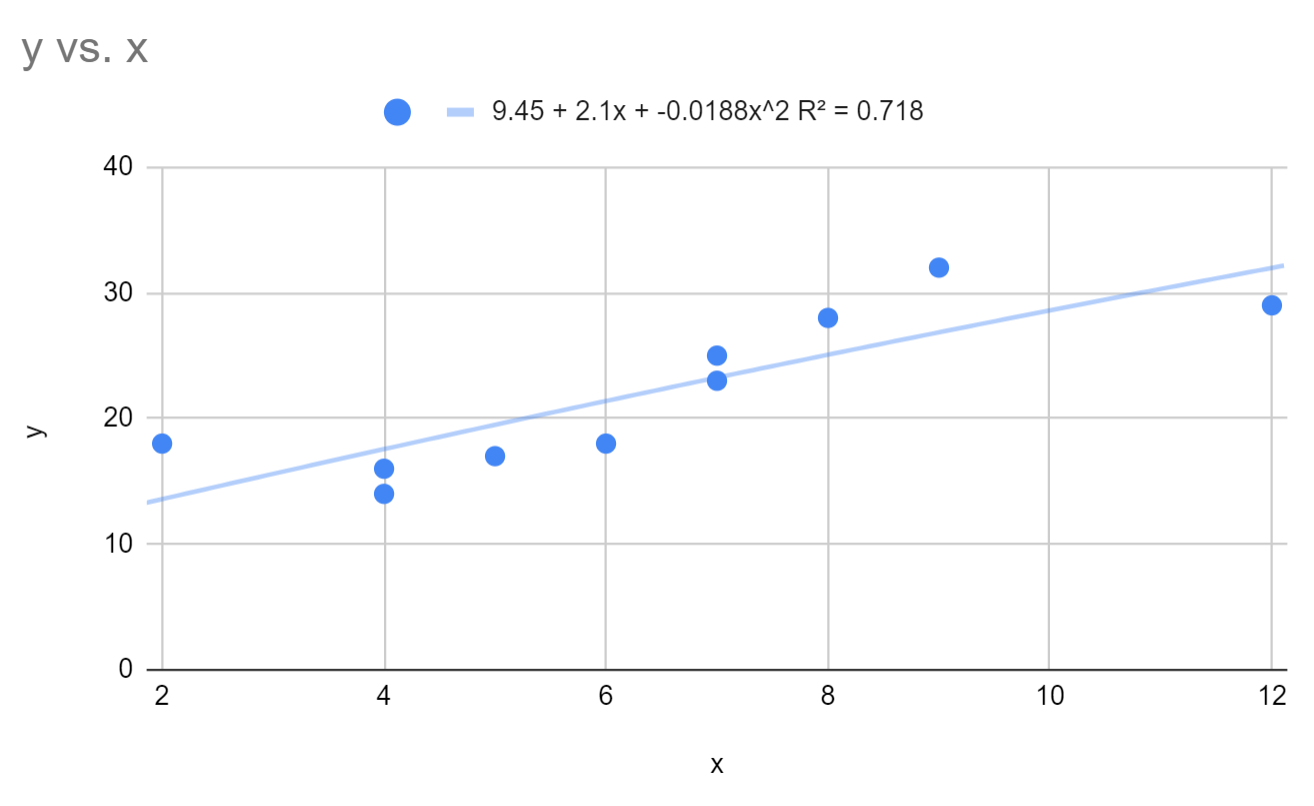
Мы видим, что подобранное уравнение полиномиальной регрессии имеет вид:
у = 9,45 + 2,1х – 0,0188х 2
R-квадрат для этой модели равен 0,718 .
Напомним, что R-квадрат показывает нам процент вариации переменной отклика, который можно объяснить переменными-предикторами. Чем выше значение, тем лучше модель.
Затем измените степень полинома на 3 в редакторе графов:
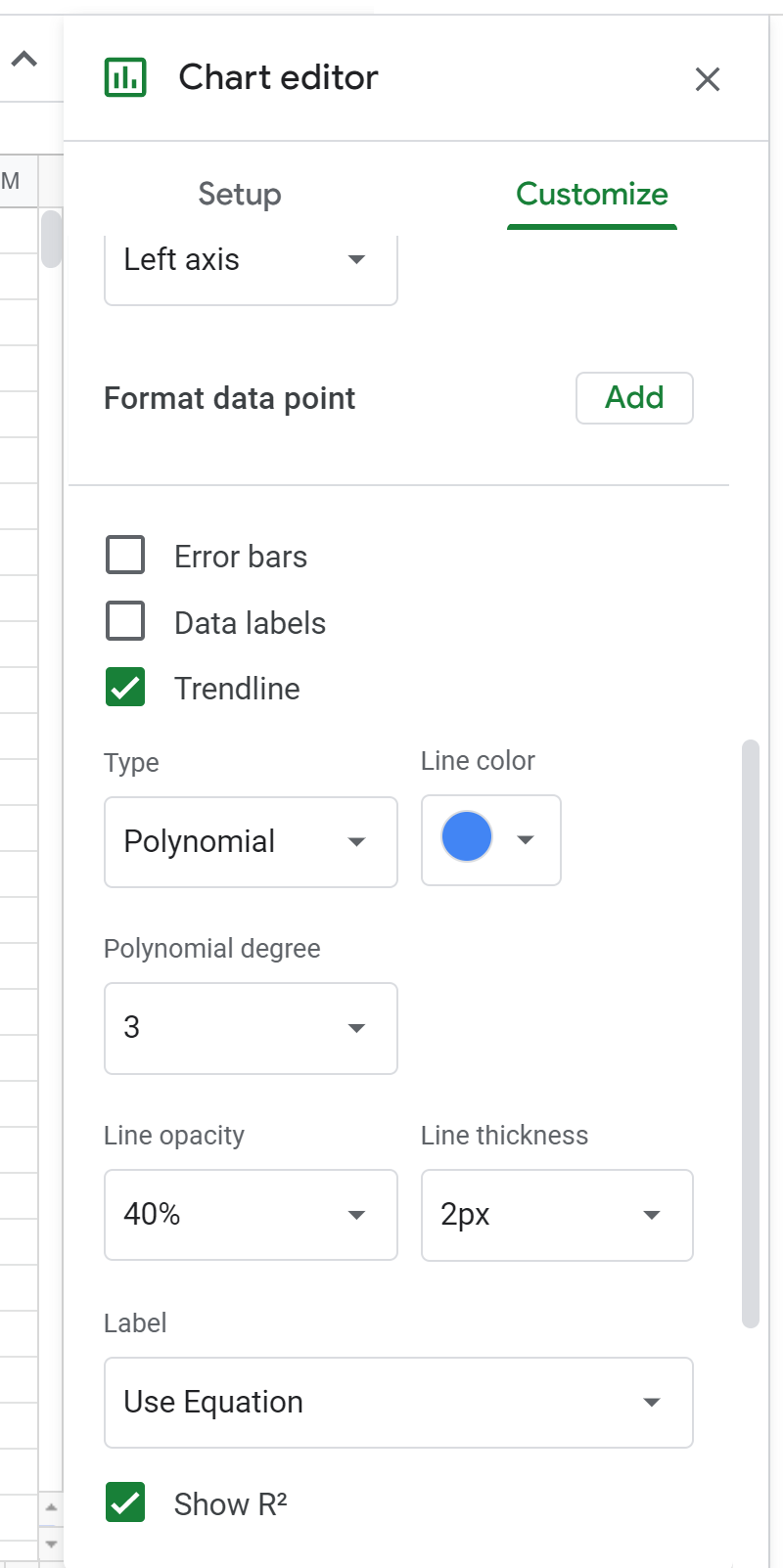
Это приведет к появлению следующей формулы над диаграммой рассеяния:
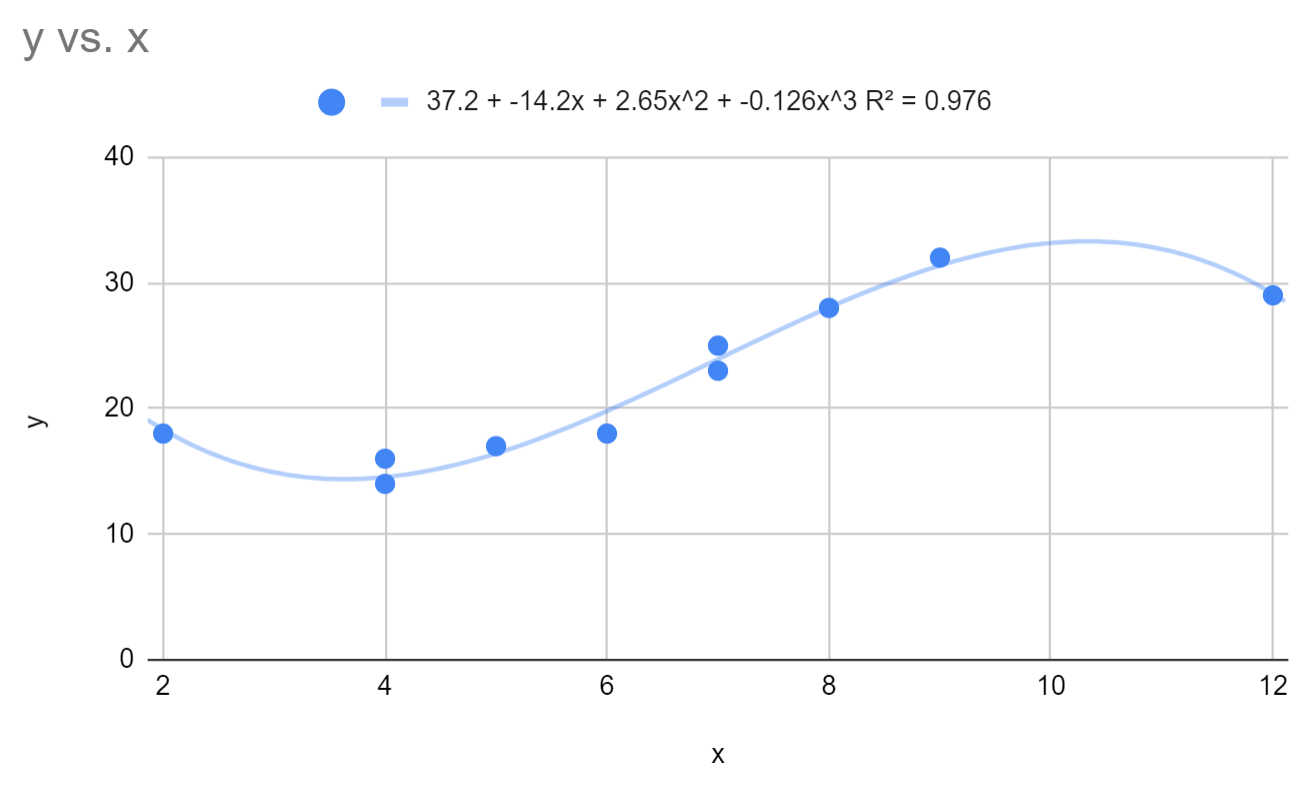
Это меняет уравнение подобранной полиномиальной регрессии на:
у = 37,2 – 14,2х + 2,64х 2 – 0,126х 3
R-квадрат для этой модели равен 0,976 .
Обратите внимание, что R-квадрат этой модели значительно выше, чем у модели полиномиальной регрессии со степенью 2. Это говорит о том, что эта модель регрессии значительно лучше улавливает тенденцию базовых данных.
Если вы измените степень полинома на 4, квадрат R едва увеличится до 0,981 . Это говорит о том, что модели полиномиальной регрессии 3-й степени достаточно, чтобы уловить тенденцию в этих данных.
Мы можем использовать подобранное уравнение регрессии, чтобы найти ожидаемое значение переменной ответа при заданном значении переменной-предиктора. Например, если x = 4, то ожидаемое значение y будет:
у = 37,2 – 14,2(4) + 2,64(4) 2 – 0,126(4) 3 = 14,576
Другие руководства по Google Sheets вы можете найти на этой странице .