Как выполнить полиномиальную регрессию с помощью scikit-learn
Полиномиальная регрессия — это метод, который мы можем использовать, когда связь между переменной-предиктором и переменной ответа является нелинейной.
Этот тип регрессии принимает форму:
Y = β 0 + β 1 X + β 2 X 2 + … + β h
где h — «степень» многочлена.
В следующем пошаговом примере показано, как выполнить полиномиальную регрессию в Python с помощью sklearn.
Шаг 1. Создайте данные
Сначала давайте создадим два массива NumPy для хранения значений предиктора и переменной ответа:
import matplotlib. pyplot as plt import numpy as np #define predictor and response variables x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]) y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]) #create scatterplot to visualize relationship between x and y plt. scatter (x,y)
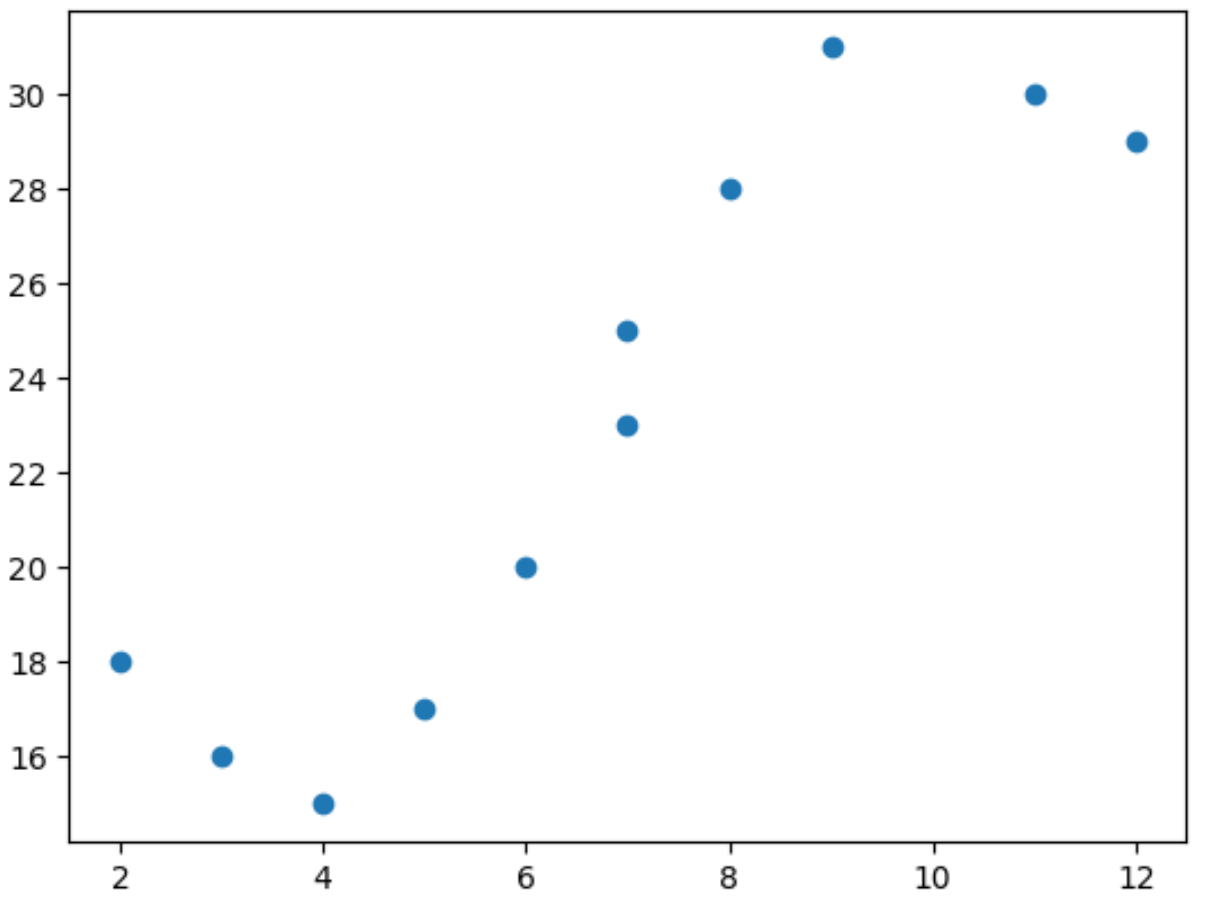
Из диаграммы рассеяния мы видим, что связь между x и y не является линейной.
Поэтому хорошей идеей будет подогнать к данным модель полиномиальной регрессии, чтобы отразить нелинейную связь между двумя переменными.
Шаг 2. Подберите модель полиномиальной регрессии
В следующем коде показано, как использовать функции sklearn для соответствия модели полиномиальной регрессии степени 3 этому набору данных:
from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression
#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )
#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))
#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)
#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )
33.62640037532282 [-11.83877127 2.25592957 -0.10889554]
Используя коэффициенты модели, показанные в последней строке, мы можем записать уравнение подобранной полиномиальной регрессии следующим образом:
у = -0,109х 3 + 2,256х 2 – 11,839х + 33,626
Это уравнение можно использовать для нахождения ожидаемого значения переменной отклика при заданном значении прогнозируемой переменной.
Например, если x равно 4, ожидаемое значение переменной ответа y будет равно 15,39:
у = -0,109(4) 3 + 2,256(4) 2 – 11,839(4) + 33,626= 15,39
Примечание . Чтобы подогнать модель полиномиальной регрессии с другой степенью, просто измените значение аргумента степени в функции PolynomialFeatures() .
Шаг 3. Визуализация модели полиномиальной регрессии
Наконец, мы можем создать простой график для визуализации модели полиномиальной регрессии, соответствующей исходным точкам данных:
#use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)
#create scatterplot of x vs. y
plt. scatter (x,y)
#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')
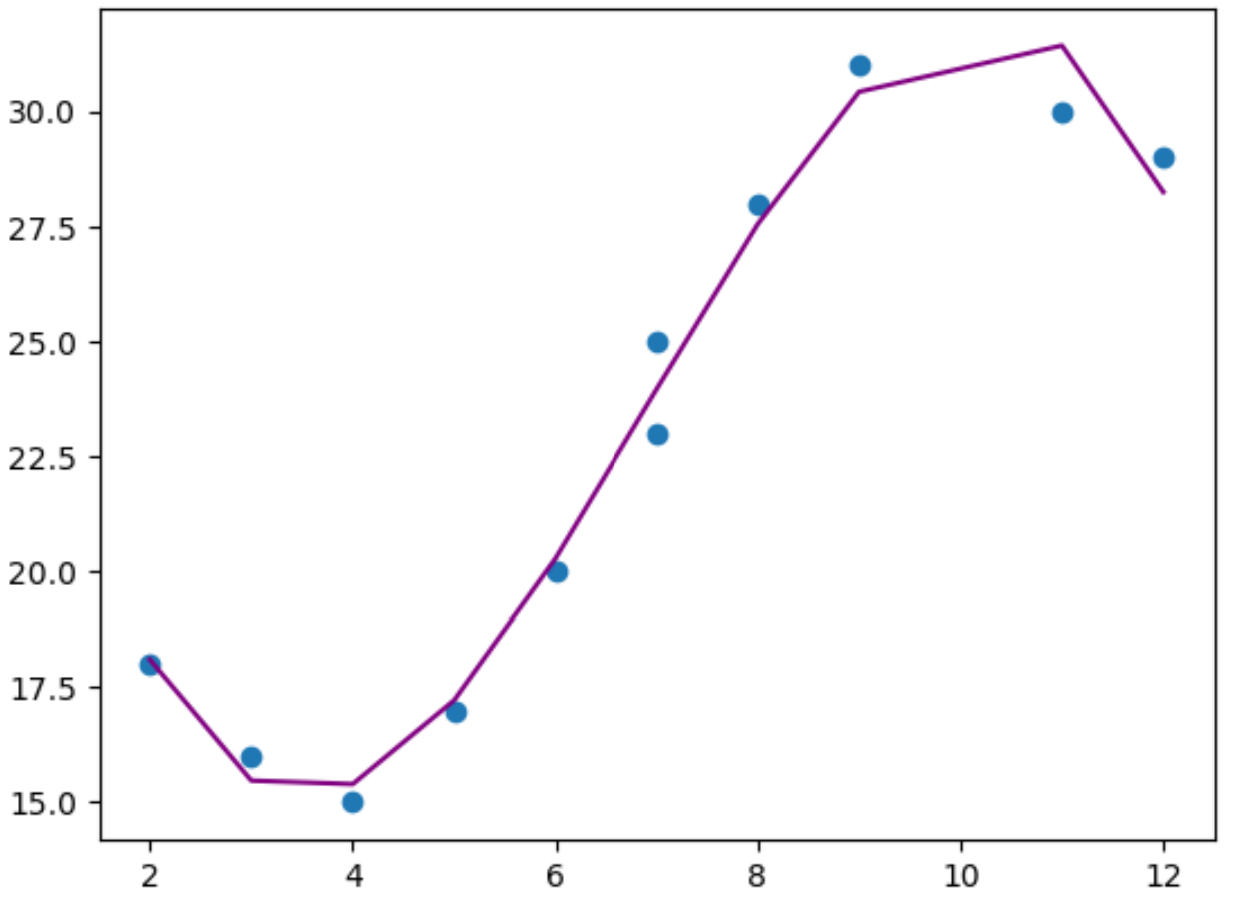
Из графика мы видим, что модель полиномиальной регрессии, похоже, хорошо соответствует данным без переобучения .
Примечание . Полную документацию по функции sklearn PolynomialFeatures() можно найти здесь .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи с помощью sklearn:
Как извлечь коэффициенты регрессии из sklearn
Как рассчитать сбалансированную точность с помощью sklearn
Как интерпретировать отчет о классификации в Sklearn