Введение в полиномиальное распределение
Полиномиальное распределение описывает вероятность получения определенного количества отсчетов для k различных результатов, когда каждый результат имеет фиксированную вероятность наступления.
Если случайную величину _ можно найти по следующей формуле:
Вероятность = n! * (p 1 x 1 * p 2 x 2 * … * p k x k ) / (x 1 ! * x 2 ! … * x k !)
Золото:
- n: общее количество событий
- x 1 : количество раз, когда возникает результат 1
- p 1 : вероятность того, что результат 1 произойдет в данном испытании.
Например, предположим, что в урне 5 красных шариков, 3 зеленых шарика и 2 синих шарика. Если мы случайным образом вытащим из урны 5 шариков с заменой, какова вероятность получить ровно 2 красных шарика, 2 зеленых шарика и 1 синий шарик?
Чтобы ответить на этот вопрос, мы можем использовать полиномиальное распределение со следующими параметрами:
- н : 5
- x 1 (# красных шариков) = 2, x 2 (# зеленых шариков) = 2, x 3 (# синих шариков) = 1
- p 1 (красная вероятность) = 0,5, p 2 (зеленая вероятность) = 0,3, p 3 (синяя вероятность) = 0,2
Подставляя эти числа в формулу, мы находим, что вероятность равна:
Вероятность = 5! * (.5 2 * .3 2 * .2 1 ) / (2! * 2! * 1!) = 0,135 .
Практические задачи полиномиального распределения
Используйте следующие практические задачи, чтобы проверить свои знания о полиномиальном распределении.
Примечание. Для расчета ответов на эти вопросы мы воспользуемся калькулятором полиномиального распределения .
Проблема 1
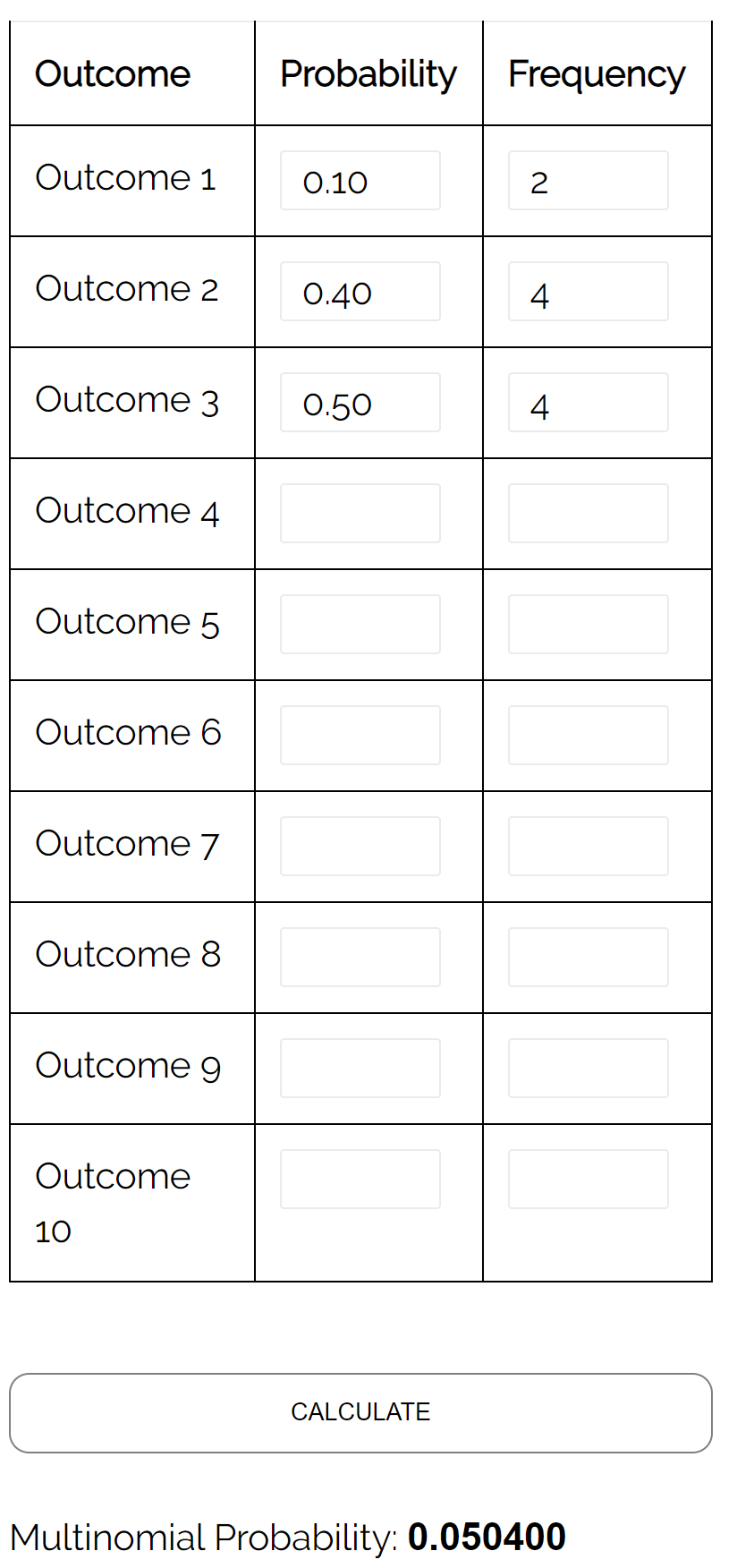
Вопрос: На трехсторонних выборах мэра кандидат А получает 10% голосов, кандидат Б — 40% голосов, кандидат С — 50% голосов. Если мы выберем случайную выборку из 10 избирателей, какова вероятность того, что 2 проголосуют за кандидата А, 4 проголосуют за кандидата В и 4 проголосуют за кандидата С?
Ответ: Используя калькулятор полиномиального распределения со следующими входными данными, мы находим, что вероятность равна 0,0504:
Проблема 2
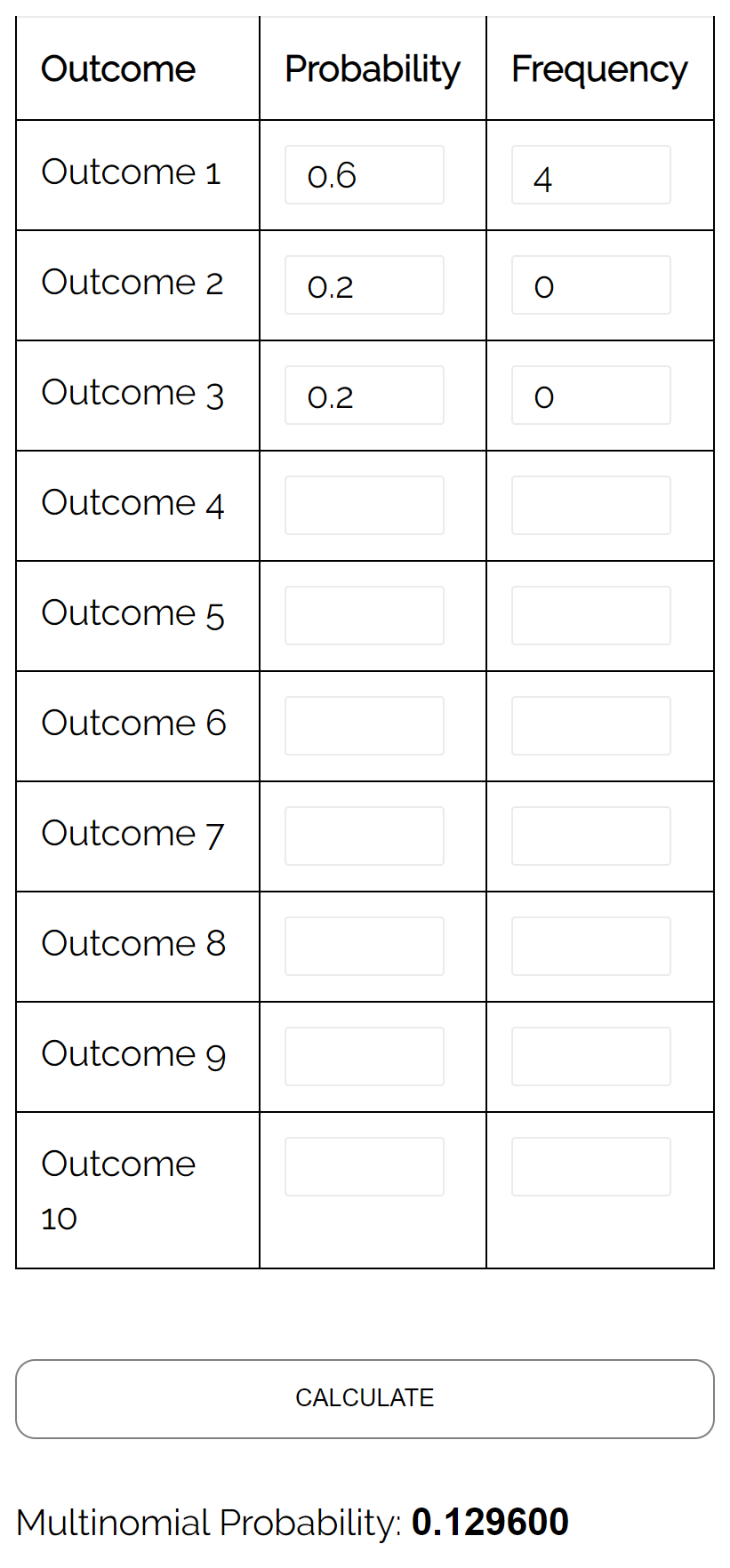
Вопрос: Предположим, в урне лежат 6 желтых шариков, 2 красных шарика и 2 розовых шарика. Если мы случайным образом выберем из урны 4 шара с заменой, какова вероятность того, что все 4 шара будут желтыми?
Ответ: Используя калькулятор полиномиального распределения со следующими входными данными, мы находим, что вероятность равна 0,1296:
Проблема 3
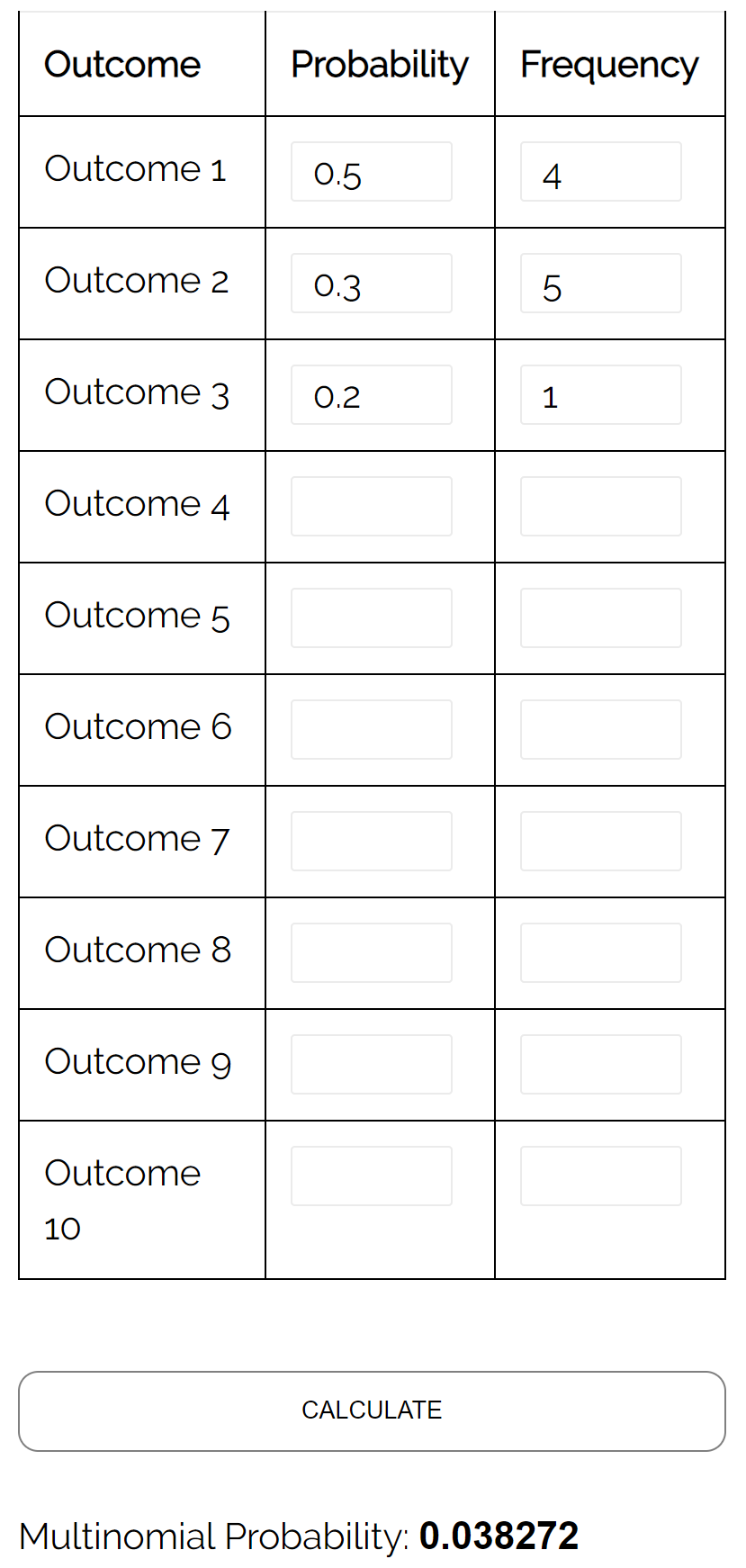
Вопрос: Предположим, два ученика играют друг против друга в шахматы. Вероятность того, что студент А выиграет данную игру, равна 0,5, вероятность того, что студент Б выиграет данную игру, равна 0,3, а вероятность того, что в данной игре будет ничья, равна 0,2. Если они сыграют 10 игр, какова вероятность того, что игрок А выиграет 4 раза, игрок Б выиграет 5 раз и что они 1 раз сравняют счет?
Ответ: Используя калькулятор полиномиального распределения со следующими входными данными, мы находим, что вероятность равна 0,038272:
Дополнительные ресурсы
Следующие учебные пособия знакомят с другими распространенными распределениями в статистике:
Введение в нормальное распределение
Введение в биномиальное распределение
Введение в распределение Пуассона
Введение в геометрическое распределение