Полуинтерквартильный размах

В этой статье объясняется, что такое полуинтерквартильный размах в статистике. Итак, вы найдете, как рассчитать полуинтерквартильный размах, решение упражнения и, кроме того, онлайн-калькулятор для расчета полуинтерквартильного размаха любой выборки данных.

Что такое полуинтерквартильный размах?

Полуинтерквартильный размах (или полуинтерквартильный размах ) равен половине разницы между первым и третьим квартилем. Следовательно, чтобы вычислить полуинтерквартильный размах, необходимо вычесть третий квартиль минус первый квартиль, а затем разделить на два.

Полуинтерквартильный размах — это мера дисперсии, которая указывает на изменчивость центральных значений. Таким образом, чем больше полуинтерквартильный диапазон набора данных, тем более разбросаны значения в центре относительно друг друга.

Одной из характеристик полуинтерквартильного размаха является то, что это надежный статистический параметр, поэтому выбросы не влияют на полуинтерквартильный размах.

Таким образом, полуинтерквартильный интервал является мерой дисперсии, аналогичной статистическому интервалу, поскольку он указывает на изменчивость набора данных путем вычитания двух значений квартиля. Однако статистический диапазон рассчитывается несколько иначе.

Формула полуинтерквартильного размаха

Полуинтерквартильный размах равен разнице между третьим квартилем и первым квартилем, разделенной на два. Следовательно, чтобы вычислить полуинтерквартильный размах, необходимо сначала найти первый и третий квартиль, затем вычесть их и, наконец, разделить результат вычитания на два.

Итак, формула расчета полуинтерквартильного размаха такова:

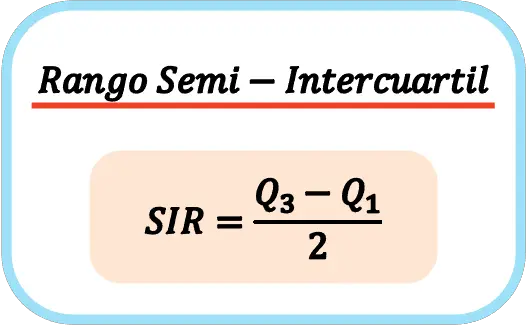
👉 Вы можете использовать калькулятор ниже, чтобы рассчитать полуинтерквартильный диапазон любого набора данных.

Обычно для обозначения полуинтерквартильного диапазона в качестве символа этой статистической меры обычно используется аббревиатура SIR ( Semi Intquartile Range ).

Короче говоря, полуинтерквартильный размах составляет половину межквартильного размаха .

Пример расчета полуинтерквартильного размаха

После ознакомления с определением полуинтерквартильного размаха и его формулой ниже приведен конкретный пример, который четко объясняет, как рассчитывается полуинтерквартильный размах.

• Мы хотим статистически проанализировать, стоит ли инвестировать в компанию. Для этого мы собрали данные о цене акций этой компании за последние 15 месяцев. В следующей таблице вы можете увидеть наблюдаемые данные, упорядоченные от наименьшего к наибольшему. Рассчитайте полуинтерквартильный диапазон этого набора данных.

Как объяснялось в разделе выше, чтобы найти полуинтерквартильный диапазон, мы должны сначала определить первый и третий квартиль.

Первый квартиль представляет собой медиану первой половины значений, что соответствует стоимости 8,95 евро/акция.

С другой стороны, третий квартиль представляет собой промежуточное значение второй половины значений, т.е. 9,83 евро/акция.

Как только мы узнаем значения первого и третьего квартилей, мы просто применяем формулу полуинтерквартильного интервала, чтобы найти его значение:

Калькулятор полуинтерквартильного размаха

Введите набор статистических данных в следующий онлайн-калькулятор, чтобы рассчитать его полуинтерквартильный диапазон. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.