Как построить график результатов множественной линейной регрессии в r

Когда мы выполняем простую линейную регрессию в R, легко визуализировать подобранную линию регрессии, потому что мы работаем только с одной переменной-предиктором и одной переменной ответа .

Например, следующий код показывает, как подогнать простую модель линейной регрессии к набору данных и построить график результатов:

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

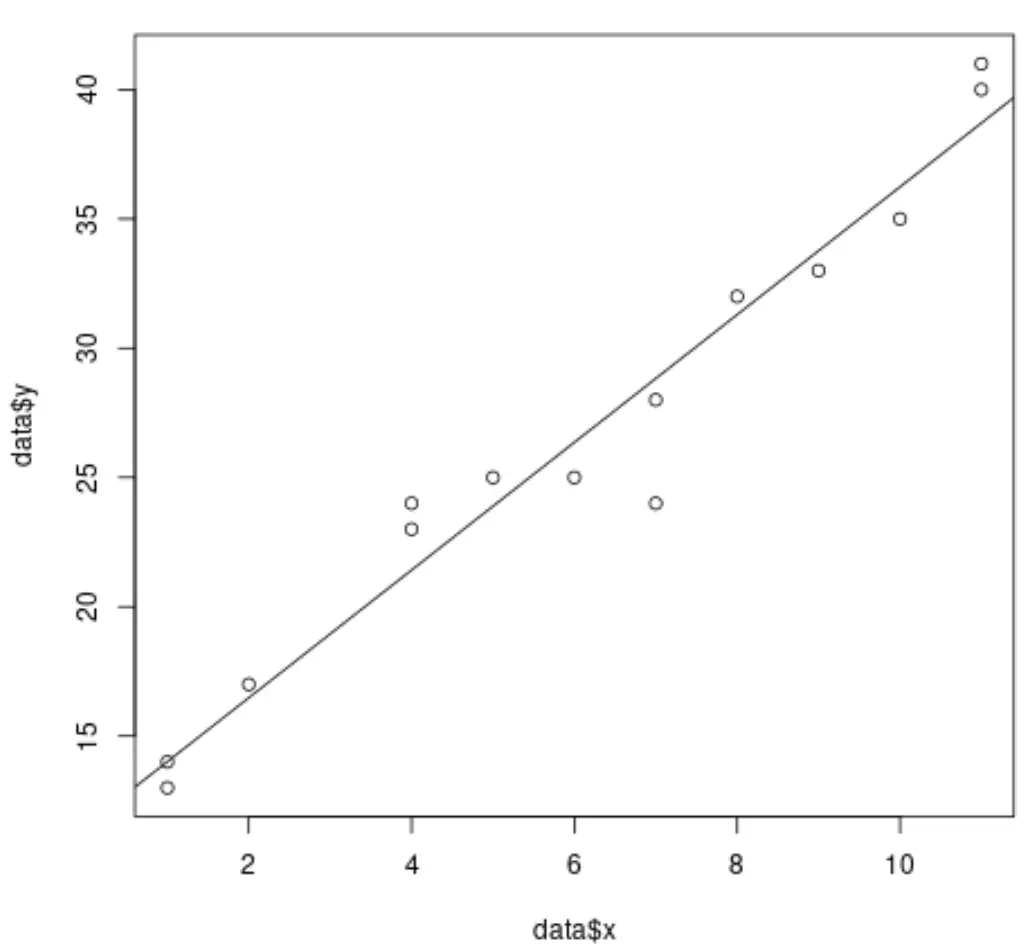
Однако когда мы выполняем множественную линейную регрессию, становится трудно визуализировать результаты, поскольку существует несколько переменных-предикторов, и мы не можем просто построить линию регрессии на двумерном графике.

Вместо этого мы можем использовать графики добавленных переменных (иногда называемые «графиками частичной регрессии»), которые представляют собой отдельные графики, которые отображают взаимосвязь между переменной ответа и переменной-предиктором, одновременно контролируя наличие других переменных-предикторов в модели .

В следующем примере показано, как выполнить множественную линейную регрессию в R и визуализировать результаты с помощью добавленных графиков переменных.

Пример. Построение графика результатов множественной линейной регрессии в R

Предположим, мы подгоняем следующую модель множественной линейной регрессии к набору данных в R, используя встроенный набор данных mtcars :

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

Из результатов мы видим, что значение p для каждого из коэффициентов меньше 0,1. Для простоты будем считать, что каждая из переменных-предикторов является значимой и должна быть включена в модель.

Чтобы построить графики добавленных переменных, мы можем использовать функцию avPlots() из пакета car :

 #load car package
library(car)

#produce added variable plots
avPlots(model)

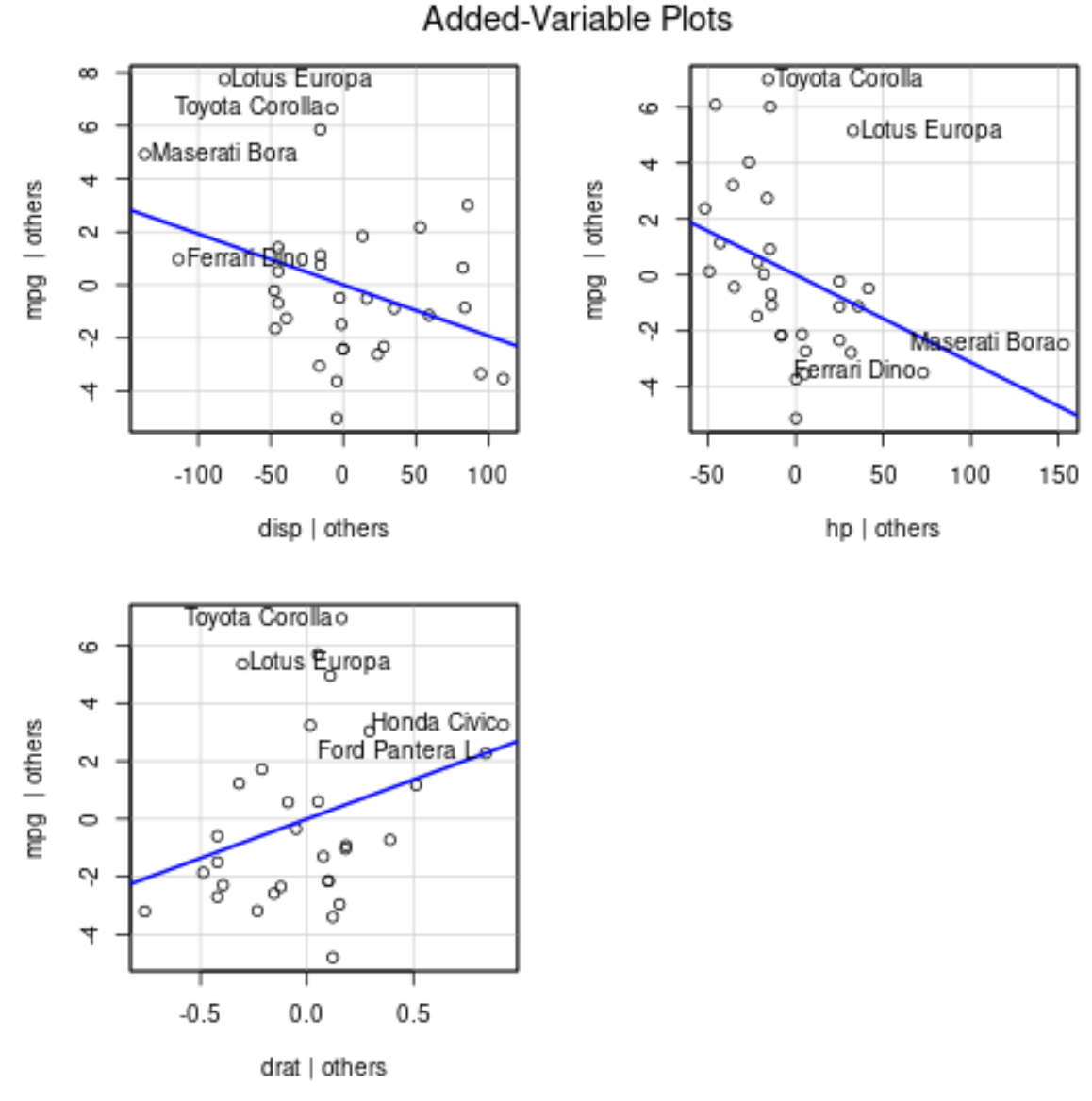
Вот как интерпретировать каждый сюжет:

• По оси X отображается одна предикторная переменная, а по оси Y отображается переменная отклика.
• Синяя линия показывает связь между переменной-предиктором и переменной ответа, при этом значения всех остальных переменных-предикторов остаются постоянными .
• Отмеченные точки на каждом графике представляют собой два наблюдения с наибольшими остатками и два наблюдения с наибольшим частичным рычагом.

Обратите внимание, что угол линии на каждом графике соответствует знаку коэффициента предполагаемого уравнения регрессии.

Например, вот предполагаемые коэффициенты для каждой предикторной переменной в модели:

• дисплей: -0,019232
• ч: -0,031229
• дата: 2.714975

Обратите внимание, что угол линии положителен на графике добавленной переменной для drat и отрицателен для disp и hp , что соответствует знакам их расчетных коэффициентов:

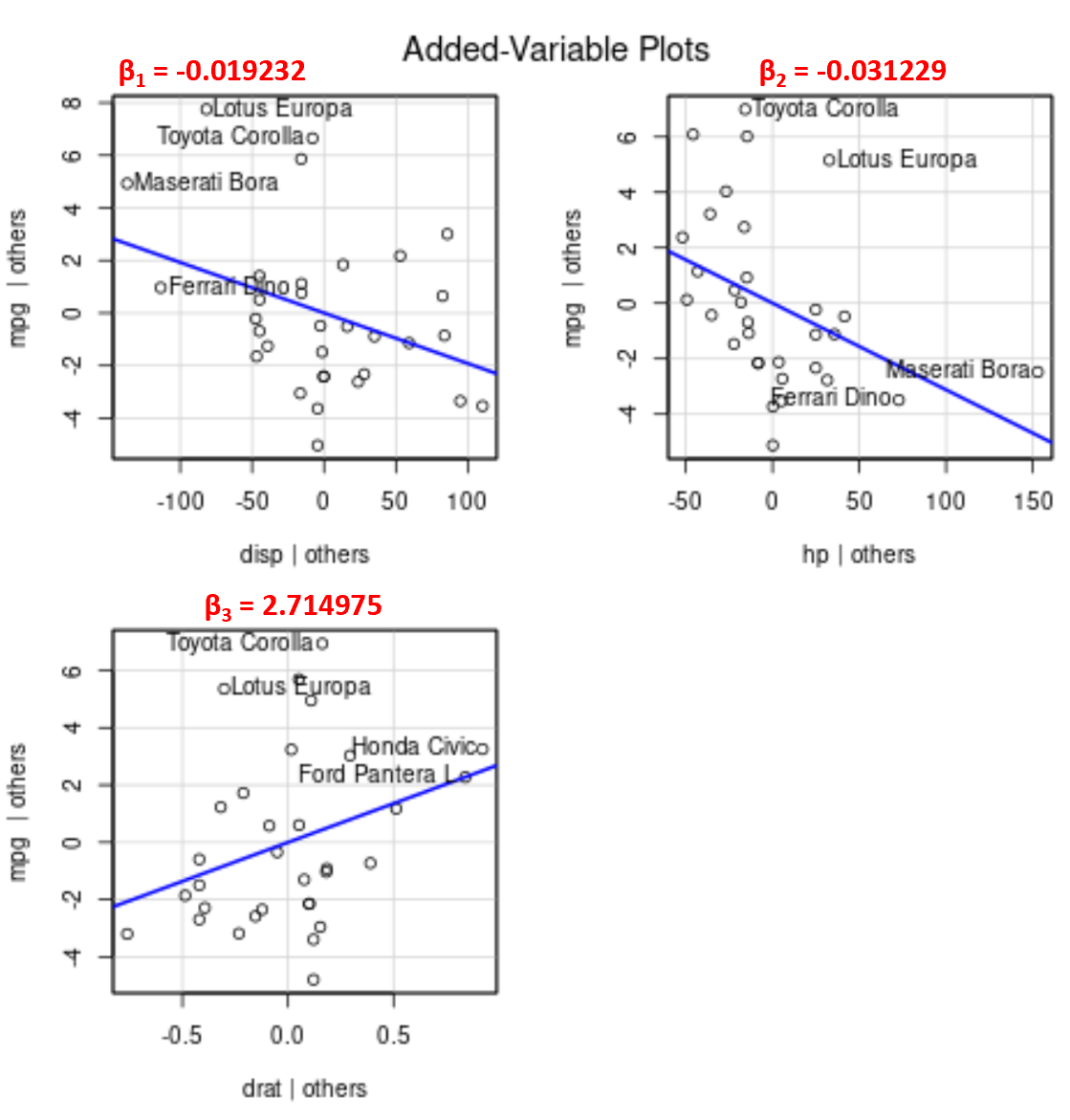
Хотя мы не можем построить одну подобранную линию регрессии на двумерном графике, поскольку у нас есть несколько переменных-предикторов, эти добавленные графики переменных позволяют нам наблюдать взаимосвязь между каждой отдельной переменной-предиктором и переменной отклика, сохраняя при этом постоянными другие переменные прогнозирования.