Почему важен размер выборки? (объяснение и примеры)
Размер выборки означает общее количество людей, участвовавших в эксперименте или исследовании.
Размер выборки важен, поскольку он напрямую влияет на точность, с которой мы можем оценить параметры популяции.
Чтобы понять, почему это так, полезно иметь общее представление о доверительных интервалах.
Краткое объяснение доверительных интервалов
В статистике мы часто стремимся измерить параметры населения – числа, которые описывают определенные характеристики всего населения.
Например, нас может заинтересовать измерение среднего роста всех жителей определенного города.
Однако зачастую сбор данных о каждом человеке в популяции обходится слишком дорого и требует много времени. Поэтому мы обычно берем случайную выборку из населения и используем данные выборки для оценки параметра совокупности.
Например, мы могли бы собрать данные о росте 100 случайных людей в городе. Затем мы можем рассчитать средний размер особей в выборке. Однако мы не можем быть уверены, что выборочное среднее точно соответствует генеральному среднему.
Чтобы учесть эту неопределенность, мы можем создать доверительный интервал . Доверительный интервал — это диапазон значений, который может содержать параметр совокупности с определенным уровнем достоверности.
Формула для расчета доверительного интервала для среднего значения совокупности:
Доверительный интервал = x +/- z*(s/√ n )
Золото:
- x : образец означает
- z: выбранное значение z
- s: выборочное стандартное отклонение
- n: размер выборки
Используемое вами значение z зависит от выбранного вами уровня достоверности. В следующей таблице показано значение z, соответствующее наиболее распространенным вариантам уровня достоверности:
| Уровень доверия | значение z |
|---|---|
| 0,90 | 1645 |
| 0,95 | 1,96 |
| 0,99 | 2,58 |
Связь между размером выборки и доверительными интервалами
Предположим, мы хотим оценить средний вес популяции черепах. Мы собираем случайную выборку черепах со следующей информацией:
- Размер выборки n = 25
- Средний вес выборки x = 300
- Выборочное стандартное отклонение s = 18,5
Вот как можно рассчитать 90% доверительный интервал для истинного среднего веса населения:
90% доверительный интервал: 300 +/- 1,645*(18,5/√ 25 ) = [293,91, 306,09]
Мы на 90% уверены, что фактический средний вес черепах в популяции составляет от 293,91 до 306,09 фунтов.
Теперь предположим, что вместо 25 черепах мы собираем данные о 50 черепахах.
Вот как можно рассчитать 90% доверительный интервал для истинного среднего веса населения:
90% доверительный интервал: 300 +/- 1,645*(18,5/√ 50 ) = [295,79, 304,30]
Обратите внимание, что этот доверительный интервал уже, чем предыдущий доверительный интервал. Это означает, что наша оценка истинного среднего веса популяции черепах более точна.
Теперь предположим, что мы собираем данные о 100 черепахах.
Вот как можно рассчитать 90% доверительный интервал для истинного среднего веса населения:
90% доверительный интервал: 300 +/- 1,645*(18,5/√ 100 ) = [296,96, 303,04]
Обратите внимание, что этот доверительный интервал даже уже, чем предыдущий доверительный интервал.
В следующей таблице приведены все значения ширины доверительного интервала:
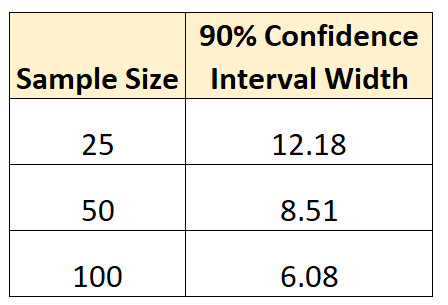
Вот итог: чем больше размер выборки, тем точнее мы можем оценить параметр совокупности .
Дополнительные ресурсы
Следующие руководства содержат более полезные объяснения доверительных интервалов и размера выборки.
Введение в доверительные интервалы
4 примера доверительных интервалов в реальной жизни
Население против. образец: в чем разница?