Пределы контроля

К бенджамин андерсон 2 августа, 2023 Управление качеством 0 комментариев

В этой статье объясняется, что такое контрольный предел и каковы различные контрольные пределы контрольной карты. Вы также увидите, как рассчитываются пределы контроля, а также рабочий пример, в котором определяются пределы контроля процесса.

Что такое контрольные пределы?

Пределы контроля — это горизонтальные линии на контрольной диаграмме, которые используются для определения того, контролируется процесс или нет.

Контрольная карта имеет два контрольных предела: верхний и нижний контрольные пределы, которые разграничивают область контроля сверху и снизу соответственно.

Итак, пределы контроля — это величины, используемые для обозначения области контроля над процессом. Если измерение, полученное в ходе процесса, находится в пределах контрольных значений, это означает, что процесс находится под контролем. В противном случае необходимо проверить машину или процесс, поскольку вполне вероятно, что они отклонились от нормы.

Виды контрольных пределов

Пределы контроля:

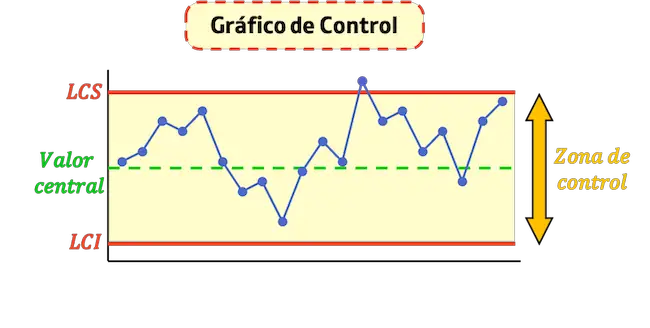
Верхний контрольный предел (LCS) : это линия, которая указывает максимальное значение, принятое в процессе.
Нижний контрольный предел (LCI) : это линия, которая указывает минимальное значение, принятое в процессе.
Центральная контрольная линия : это линия, которая представляет среднее значение графика. Чем ближе точки к этой линии, тем стабильнее процесс.

Как рассчитать пределы контроля

В настоящее время пределы контроля процесса обычно рассчитываются с помощью компьютерного программного обеспечения, которое позволяет управлять процессом. Однако также важно знать, как они рассчитываются, поскольку вам может потребоваться найти их вручную.

Расчет контрольных пределов контрольной карты зависит от типа диаграммы, которую вы хотите создать, поскольку значения будут меняться в зависимости от того, является ли это контрольной картой для среднего значения или для диапазона.

Диаграмма среднего контроля представляет собой график, на котором оценивается эволюция среднего значения процесса. Итак, среднее значение набора значений рассчитывается по следующей формуле:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Золото:

$x_i$

– номер меры i.
$n$

это количество выполненных измерений.

Обозначим центральное значение контрольной карты для среднего как

$\overline{\overline{X}}$

, которое представляет собой среднее значение выборок и рассчитывается по следующему выражению:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Золото:

$\overline{X}_j$

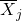
среднее значение выборки j.
$m$

— количество взятых образцов.

➤ См.: Вычисление среднего арифметического.

Напротив, центральное значение контрольной диаграммы экстента — это среднее значение экстента всех взятых образцов:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Золото:

$R_j$

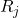
— диапазон выборки j.
$m$

— количество взятых образцов.

➤ См.: Расчет статистического диапазона.

Таким образом, формулы расчета пределов контроля контрольной карты имеют следующий вид:

контрольная карта

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

Карта управления R

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Где значения параметров A ₂ , D ₃ и D ₄ находятся в следующей таблице:

Размер (№)	В ₂	День ₃	_Д4
2	1880	0,000	3267
3	1023	0,000	2575
4	0,729	0,000	2282
5	0,577	0,000	2115
6	0,483	0,000	2004 г.
7	0,419	0,076	1924
8	0,373	0,136	1864
9	0,337	0,184	1816
десять	0,308	0,223	1777

Пример расчета контрольных пределов

Промышленная компания желает контролировать измерение диаметра цилиндра, чтобы убедиться, что его производственный процесс находится под контролем. Для этого каждые 15 минут отбирайте пробу из 5 цилиндров и измеряйте их диаметр. В следующей таблице показаны записи измерений.

Для нахождения пределов контроля необходимо сначала взять среднее арифметическое и размах каждого набора измерений:

Теперь вычислим среднее значение средних и диапазонов, которые будут центральными значениями контрольной диаграммы для среднего и для диапазона соответственно:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

В этом случае каждая выборка состоит из 5 измерений, поэтому коэффициенты формул контрольного предела будут следующими:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Рассчитаем верхнюю и нижнюю контрольные границы средней и расширенной контрольной карты:

Контрольная таблица Контрольные пределы

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Контрольные пределы Карта управления R

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

Таким образом, карты контроля упражнений выглядят следующим образом:

На первой контрольной диаграмме мы видим, что на два значения меньше нижнего контрольного предела. Кроме того, на второй контрольной диаграмме также имеется значение выше верхнего контрольного предела. Поэтому процесс не контролируется.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что такое контрольные пределы?

Виды контрольных пределов

Как рассчитать пределы контроля

Пример расчета контрольных пределов

Об авторе

бенджамин андерсон

Добавить комментарий