Что такое пространство выборки? определение и примеры
Выборочное пространство эксперимента — это совокупность всех возможных результатов эксперимента.
Например, предположим, что мы один раз бросаем игральную кость. Выборочное пространство возможных результатов включает в себя:
Выборочное пространство = 1, 2, 3, 4, 5, 6
Используя обозначения, мы пишем символ выборочного пространства курсивом S, а результаты заключаем в круглые скобки следующим образом:
S = {1, 2, 3, 4, 5, 6}
Примеры выборочных пространств
Вот несколько дополнительных примеров примеров пространств:
Пример 1: нарисовать
Предположим, мы один раз подбросили монету. Если мы положим H = монета упадет орлом, а T = монета упадет решкой, то пространство выборки для этого подбрасывания монеты будет:
S = {H, Т}
Пример 2: шарики в мешочке
Предположим, мы случайным образом выбираем шарик из мешка, содержащего три шарика: красный шарик, зеленый шарик и синий шарик. Если мы положим R = красный, G = зеленый и B = синий, то пространство выборки будет:
S = {R, G, B}
Пример 3. Подбрасывание монеты и бросок кубика.
Предположим, мы одновременно подбрасываем монету и бросаем игральную кость. Если мы позволим H1 представлять результат «Head» и «1», то пространство выборки для результатов будет:
S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
Основной принцип подсчета
Фундаментальный принцип подсчета — это способ подсчета общего числа потенциальных результатов эксперимента.
Этот принцип гласит, что если событие A имеет n различных исходов, а событие B имеет m различных исходов, то общее количество потенциальных исходов можно рассчитать следующим образом:
Всего результатов = m * n
Пример 1. Подбрасывание монеты и бросок игральной кости.
Например, если мы одновременно подбрасываем монету и бросаем игральную кость, то общее количество результатов в выборочном пространстве можно рассчитать следующим образом:
Общие результаты = (2 варианта выпадения монеты) * (6 вариантов выпадения кубика) = 12 возможных исходов.
Мы записали эти 12 результатов в предыдущем примере:
S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
Пример 2. Подсчет комбинаций нарядов
Этот принцип также можно использовать для расчета общих результатов в выборочном пространстве для более чем двух событий.
Например, предположим, что в случайном ящике лежат 3 разные рубашки, 4 разных брюк и 2 разных носка. Если мы случайным образом выберем по одному предмету одежды, не глядя, общее количество возможных нарядов будет рассчитано следующим образом:
Всего нарядов = 3 * 4 * 2 = 24 возможных наряда.
Визуализация выборочных пространств с помощью древовидных диаграмм
Если количество результатов в выборочном пространстве велико, может оказаться полезным построить древовидную диаграмму для визуализации различных комбинаций результатов.
Например, предположим, что в шкафу есть 2 разные рубашки, 2 разных брюк и 2 разных носка. Если мы случайным образом выберем по одному предмету одежды, не глядя, общее количество возможных нарядов можно представить следующим образом:
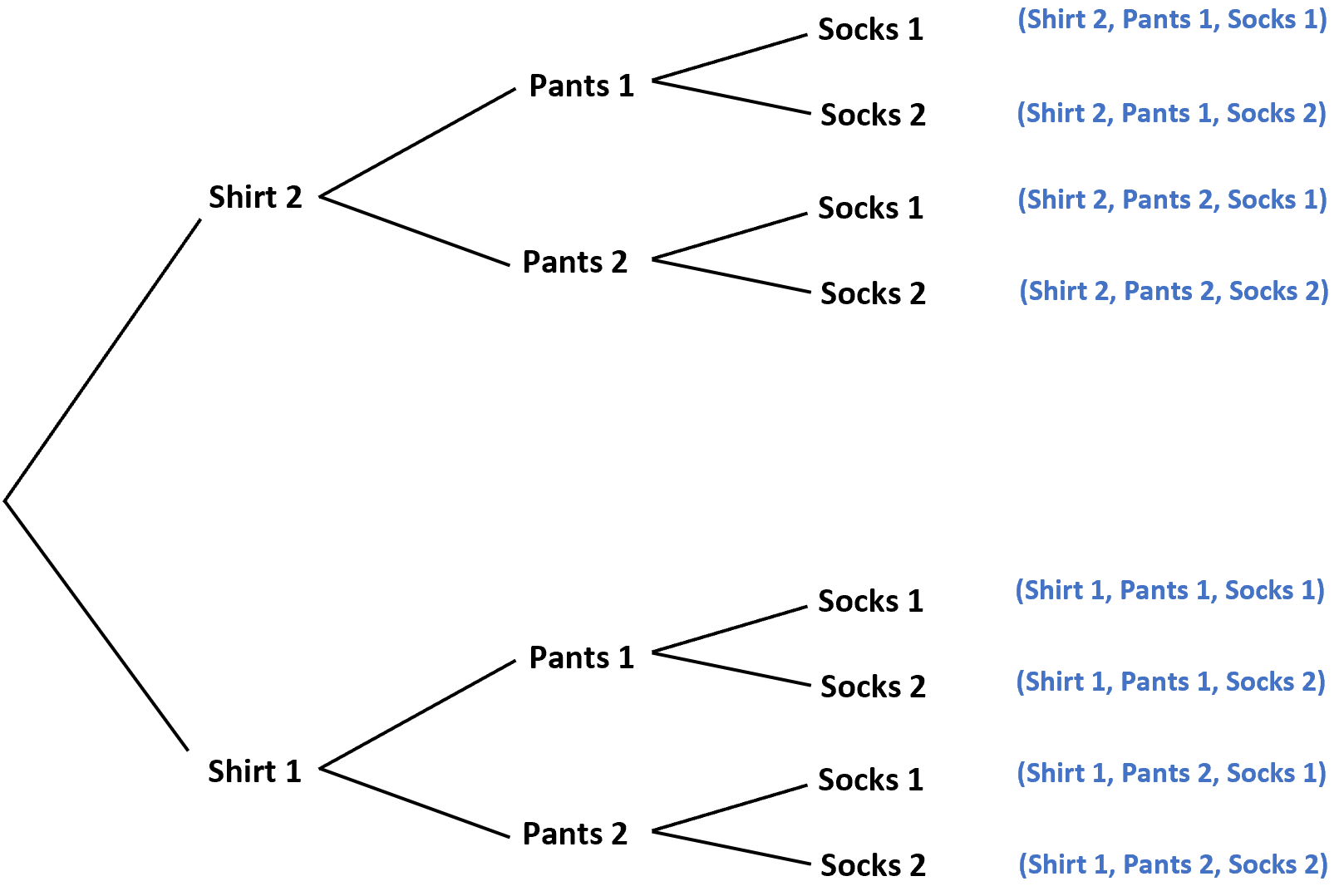
Эта диаграмма помогает нам визуализировать восемь различных потенциальных результатов в пространстве выборки.
Мы также можем использовать фундаментальный принцип подсчета, чтобы подтвердить, что должно быть восемь различных результатов:
Общий результат = 2 рубашки * 2 штана * 2 носка = 8 возможных нарядов.
Вычисление вероятностей исхода в выборочных пространствах
Определив выборочное пространство эксперимента, мы можем рассчитать вероятность возникновения события А , используя следующую формулу:
P(A) = (Пространство выборки A) / (Общее пространство выборки)
Например, предположим, что мы один раз бросаем игральную кость. Пространство выборки можно записать в виде:
S = {1, 2, 3, 4, 5, 6}
Если мы определим событие A как выпадение кубика на число «2», то пространство выборки события A можно записать следующим образом:
С = {2}
Таким образом, вероятность наступления события А можно рассчитать следующим образом:
Р(А) = 1/6
Если мы определим событие A как выпадение кубика с четным числом, то пространство выборки события A можно записать следующим образом:
С = {2, 4, 6}
Таким образом, вероятность наступления события А можно рассчитать следующим образом:
Р(А) = 3/6