Введение в распределение пуассона
Распределение Пуассона — одно из самых популярных распределений в статистике.
Чтобы понять распределение Пуассона, полезно сначала понять эксперименты Пуассона.
Рыбные эксперименты
Эксперимент Пуассона — это эксперимент, обладающий следующими свойствами:
- Количество успехов эксперимента можно подсчитать.
- Известно среднее количество успехов, произошедших за определенный временной (или пространственный) интервал.
- Каждый результат независим.
- Вероятность успешного возникновения пропорциональна размеру интервала.
Примером эксперимента Пуассона является количество родов в час в данной больнице. Например, предположим, что в конкретной больнице в среднем происходит 10 родов в час. Это эксперимент Пуассона, поскольку он обладает следующими четырьмя свойствами:
- Число успехов эксперимента можно посчитать – Мы можем посчитать число рождений.
- Известно среднее количество рождений, происходящих в течение определенного интервала времени. Известно, что в час в среднем происходит 10 рождений.
- Каждый результат независим. Вероятность того, что одна мать родит в данный час, не зависит от вероятности того, что родит другая мать.
- Вероятность наступления успеха пропорциональна размеру интервала: чем длиннее временной интервал, тем выше вероятность рождения ребенка.
Мы можем использовать распределение Пуассона, чтобы ответить на вопросы о вероятностях этого эксперимента Пуассона, такие как:
- Какова вероятность того, что за один час произойдет более 12 родов?
- Какова вероятность того, что за данный час произойдет менее 5 родов?
- Какова вероятность того, что за данный час произойдет от 8 до 11 родов?
Распределение рыбы
Распределение Пуассона описывает вероятность получения k успехов в течение заданного интервала времени.
Если случайная величина X подчиняется распределению Пуассона, то вероятность того, что X = k успеха, можно найти по следующей формуле:
P(X=k) = λ k * e – λ / k!
Золото:
- λ: среднее количество успехов, произошедших за определенный интервал.
- k: количество успехов
- е: константа, равная примерно 2,71828
Например, предположим, что в конкретной больнице в среднем рождаются 2 ребенка в час. Мы можем использовать приведенную выше формулу, чтобы определить вероятность рождения 0, 1, 2, 3 и т. д. в данный час:
P(X=0) = 2 0 * e – 2/0 ! = 0,1353
P(X=1) = 2 1 * e – 2/1 ! = 0,2707
P(X=2) = 2 2 * e – 2/2 ! = 0,2707
P(X=3) = 2 3 * e – 2/3 ! = 0,1805
Мы можем вычислить вероятность любого количества рождений вплоть до бесконечности. Затем мы создаем простую гистограмму для визуализации этого распределения вероятностей:

Расчет кумулятивных вероятностей Пуассона
Единую вероятность Пуассона (например, вероятность того, что в больнице произойдет 3 родов в течение определенного часа) несложно вычислить, используя приведенную выше формулу, но для расчета кумулятивных вероятностей Пуассона нам нужно сложить отдельные вероятности.
Например, предположим, что мы хотим знать вероятность того, что в больнице будет 1 или меньше родов в течение определенного часа. Для расчета этой вероятности мы будем использовать следующую формулу:
P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406
Это называется кумулятивной вероятностью , поскольку предполагает сложение нескольких вероятностей. Мы можем рассчитать кумулятивную вероятность рождения k или меньшего числа рождений за данный час, используя аналогичную формулу:
P(X≤0) = P(X=0) = 0,1353
P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406
P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767
Мы можем вычислить эти совокупные вероятности для любого числа рождений вплоть до бесконечности. Затем мы можем создать гистограмму для визуализации этого кумулятивного распределения вероятностей:
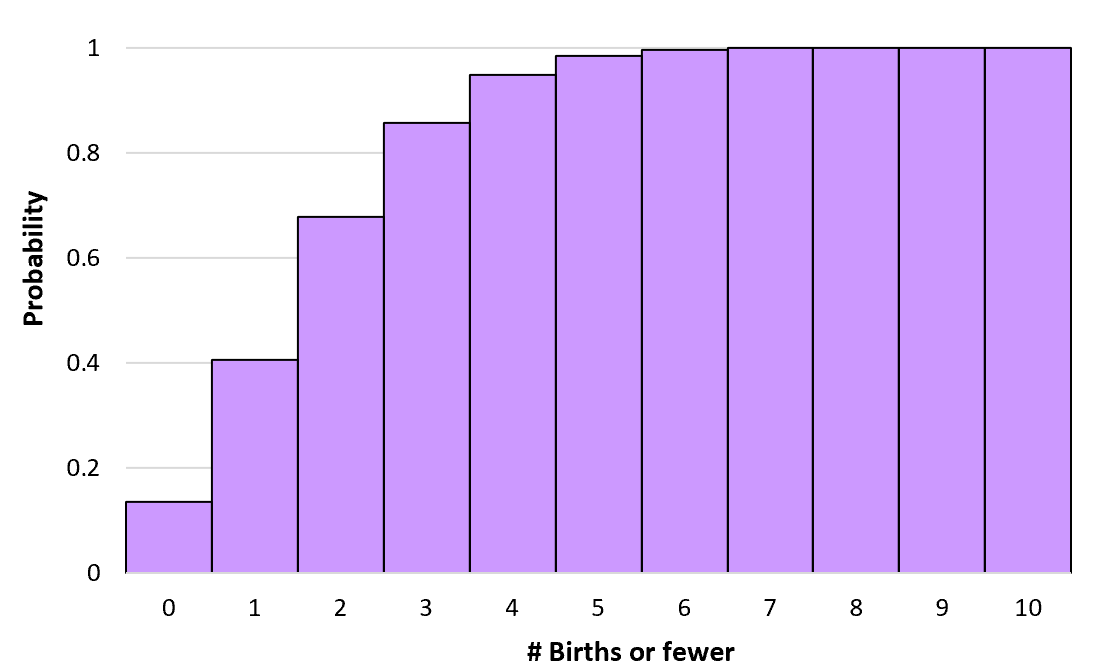
Свойства распределения Пуассона
Распределение Пуассона обладает следующими свойствами:
Среднее значение распределения равно λ .
Дисперсия распределения также равна λ .
Стандартное отклонение распределения равно √ λ .
Например, предположим, что в больнице в среднем рождаются 2 ребенка в час.
Среднее число рождений, ожидаемых в данный час, составляет λ = 2 рождения.
Дисперсия ожидаемого нами числа рождений составляет λ = 2 рождения.
Проблемы практики распределения рыбы
Используйте следующие практические задачи, чтобы проверить свои знания о распределении Пуассона.
Примечание. Для расчета ответов на эти вопросы мы воспользуемся калькулятором распределения Пуассона .
Проблема 1
Вопрос: Мы знаем, что определенный сайт совершает 10 продаж в час. Какова вероятность того, что за час сайт совершит ровно 8 продаж?
Ответ: Используя калькулятор распределения Пуассона с λ = 10 и x = 8, мы находим, что P(X=8) = 0,1126 .
Проблема 2
Вопрос: Мы знаем, что определенный агент по недвижимости совершает в среднем 5 продаж в месяц. Какова вероятность того, что в течение данного месяца она совершит более 7 продаж?
Ответ: Используя калькулятор распределения Пуассона при λ = 5 и x = 7, мы находим, что P(X>7) = 0,13337 .
Проблема 3
Вопрос: Мы знаем, что в одной больнице происходит 4 роды в час. Какова вероятность того, что в течение данного часа родится 4 или менее детей?
Ответ: Используя калькулятор распределения Пуассона при λ = 4 и x = 4, мы находим, что P(X≤4) = 0,62884 .
Дополнительные ресурсы
В следующих статьях объясняется, как использовать распределение Пуассона в различных статистических программах:
Как использовать распределение Пуассона в R
Как использовать распределение Пуассона в Excel
Как рассчитать вероятности Пуассона на калькуляторе TI-84
Реальные примеры распределения Пуассона
Калькулятор распределения рыбы