Доверительный интервал для разницы между средними значениями

Доверительный интервал (ДИ) для разницы между средними значениями — это диапазон значений, который может содержать истинную разницу между двумя средними значениями совокупности с определенным уровнем достоверности.

В этом руководстве объясняется следующее:

• Мотивация создания этого доверительного интервала.
• Формула для создания этого доверительного интервала.
• Пример того, как рассчитать этот доверительный интервал.
• Как интерпретировать этот доверительный интервал.

ДИ для разницы между средствами: мотивация

Исследователи часто хотят оценить разницу между средними значениями двух популяций. Чтобы оценить эту разницу, они соберут случайную выборку из каждой популяции и рассчитают среднее значение для каждой выборки. Затем они могут сравнить разницу между двумя средними значениями.

Однако они не могут знать наверняка, соответствует ли разница между выборочными средними истинным различиям между генеральными средними. Вот почему они могут создать доверительный интервал для разницы между двумя средними значениями. Это обеспечивает диапазон значений, который, вероятно, будет содержать истинную разницу между средними значениями совокупности.

Например, предположим, что мы хотим оценить разницу в среднем весе двух разных видов черепах. Поскольку в каждой популяции насчитываются тысячи черепах, было бы слишком долго и дорого взвешивать каждую черепаху по отдельности.

Вместо этого мы могли бы взять простую случайную выборку из 15 черепах из каждой популяции и использовать средний вес каждой выборки, чтобы оценить истинную разницу в среднем весе между двумя популяциями:

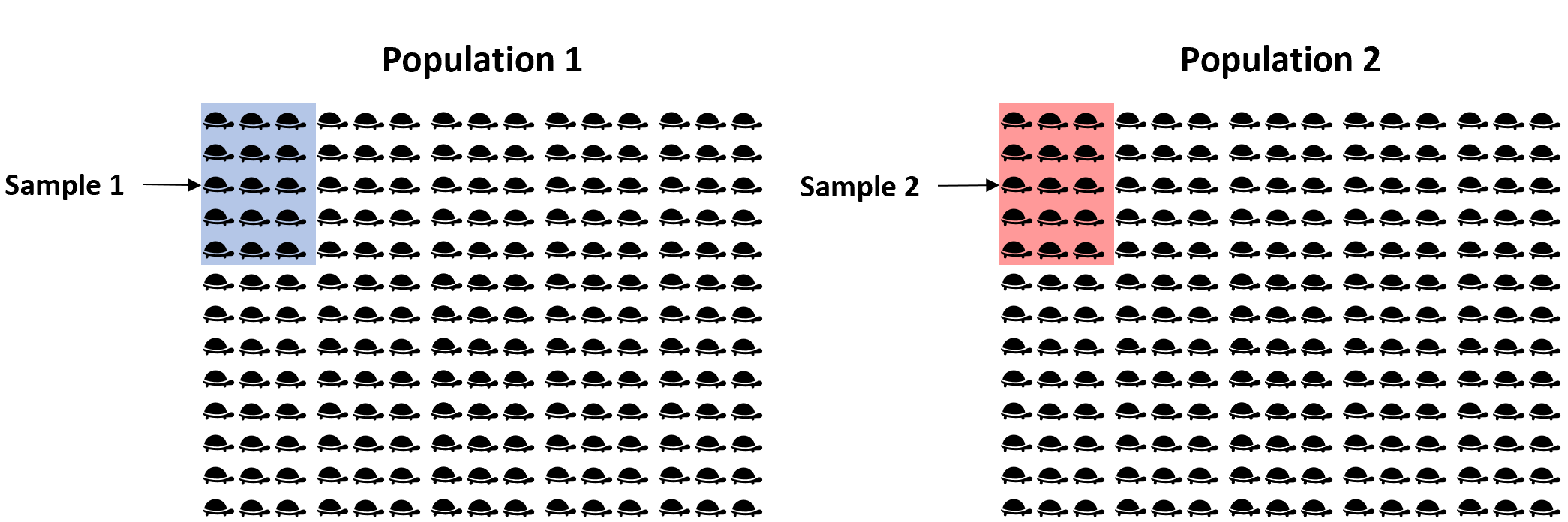
Проблема в том, что наши выборки случайны, поэтому нет гарантии, что разница в среднем весе между двумя выборками точно соответствует разнице в среднем весе между двумя популяциями. Итак, чтобы уловить эту неопределенность, мы можем создать доверительный интервал, содержащий диапазон значений, который, вероятно, будет содержать истинную разницу в среднем весе между двумя популяциями.

ДИ для разницы между средними значениями: формула

Мы используем следующую формулу для расчета доверительного интервала для разницы между двумя средними значениями:

Доверительный интервал = ( x ₁ – x ₂ ) +/- t*√((s _p ² /n ₁ ) + (s _p ² /n ₂ ))

Золото:

• x ₁ , x ₂ : среднее значение образца 1, среднее значение образца 2
• t: t-критическое значение, основанное на уровне достоверности и (n ₁ + n ₂ -2) степенях свободы.
• s _p ² : объединенная дисперсия
• n ₁ , n ₂ : размер выборки 1, размер выборки 2

Золото:

• Объединенная дисперсия рассчитывается следующим образом: s _p ² = ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² ) / (n ₁ +n ₂ -2)
• Критическое значение t можно найти с помощью калькулятора обратного распределения t.

ДИ для разницы между средними значениями: пример

Предположим, мы хотим оценить разницу в среднем весе двух разных видов черепах. Поэтому мы соберем случайную выборку из 15 черепах из каждой популяции. Вот сводные данные по каждому образцу:

Образец 1:

• х1 = ₃₁₀
• с ₁ = 18,5
• п ₁ = 15

Образец 2:

• х2 ₌ 300
• _с2 = 16,4
• _п2 = 15

Вот как найти различные доверительные интервалы для истинной разницы в средних весах населения:

90% доверительный интервал:

(310-300) +/- 1,70*√((305,61/15) + (305,61/15)) = [-0,8589, 20,8589]

95% доверительный интервал:

(310-300) +/- 2,05*√((305,61/15) + (305,61/15)) = [-3,0757, 23,0757]

99% доверительный интервал:

(310-300) +/- 2,76*√((305,61/15) + (305,61/15)) = [-7,6389, 27,6389]

Примечание. Вы также можете найти эти доверительные интервалы с помощью калькулятора статистического доверительного интервала для разницы между средними значениями .

Вы заметите, что чем выше уровень достоверности, тем шире доверительный интервал. Это должно иметь смысл, поскольку более широкие интервалы с большей вероятностью будут содержать истинное среднее значение численности населения, поэтому мы более «уверены», что интервал содержит истинное среднее значение численности населения.

ДИ для разницы между средними : интерпретация

Мы интерпретируем доверительный интервал следующим образом:

Существует 95% вероятность того, что доверительный интервал [-3,0757, 23,0757] содержит истинную разницу в среднем весе между двумя популяциями черепах.

Поскольку этот интервал содержит значение «0», это означает, что возможно отсутствие разницы в среднем весе между черепахами из этих двух популяций. Другими словами, мы не можем с уверенностью 95% сказать, что существует разница в среднем весе между черепахами из этих двух популяций.