Распределение стьюдента
В этой статье объясняется, что такое распределение Стьюдента и для чего оно используется. Кроме того, показан график t-распределения Стьюдента и каковы характеристики этого типа распределения вероятностей.
Каково распределение Стьюдента?
Распределение Стьюдента — это распределение вероятностей, широко используемое в статистике. В частности, t-распределение Стьюдента используется в t-критерии Стьюдента для определения разницы между средними значениями двух выборок и установления доверительных интервалов.
Распределение Стьюдента было разработано статистиком Уильямом Сили Госсетом в 1908 году под псевдонимом «Студент».
Распределение Стьюдента определяется количеством степеней свободы, полученным путем вычитания одной единицы из общего числа наблюдений. Следовательно, формула для определения степеней свободы t-распределения Стьюдента имеет вид ν=n-1 .
![Rendered by QuickLaTeX.com \begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png)
График распределения Стьюдента
Теперь, когда мы знаем определение t-распределения Стьюдента, давайте посмотрим, каков его график. Итак, ниже вы можете графически увидеть несколько примеров t-распределений Стьюдента с разными степенями свободы.
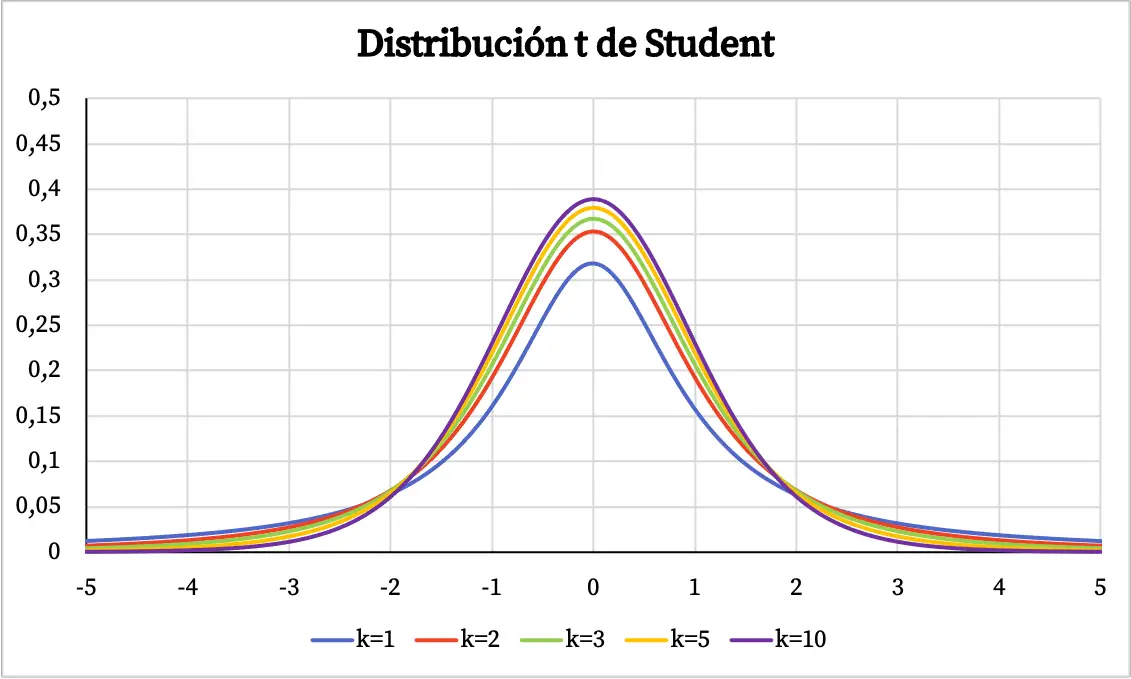
Из графика распределения Стьюдента можно вывести следующие свойства:
- Распределение Стьюдента симметрично с центром в точке 0 и имеет колоколообразную форму.
- Распределение Стьюдента более дисперсно, чем нормальное, то есть кривая распределения Стьюдента шире.
- Чем больше степеней свободы имеет t-распределение Стьюдента, тем меньше его дисперсия.
На графике выше функция плотности t-распределения Стьюдента изображена в зависимости от его степеней свободы. Однако ниже вы можете увидеть, как меняется кумулятивная функция вероятности t-распределения Стьюдента:
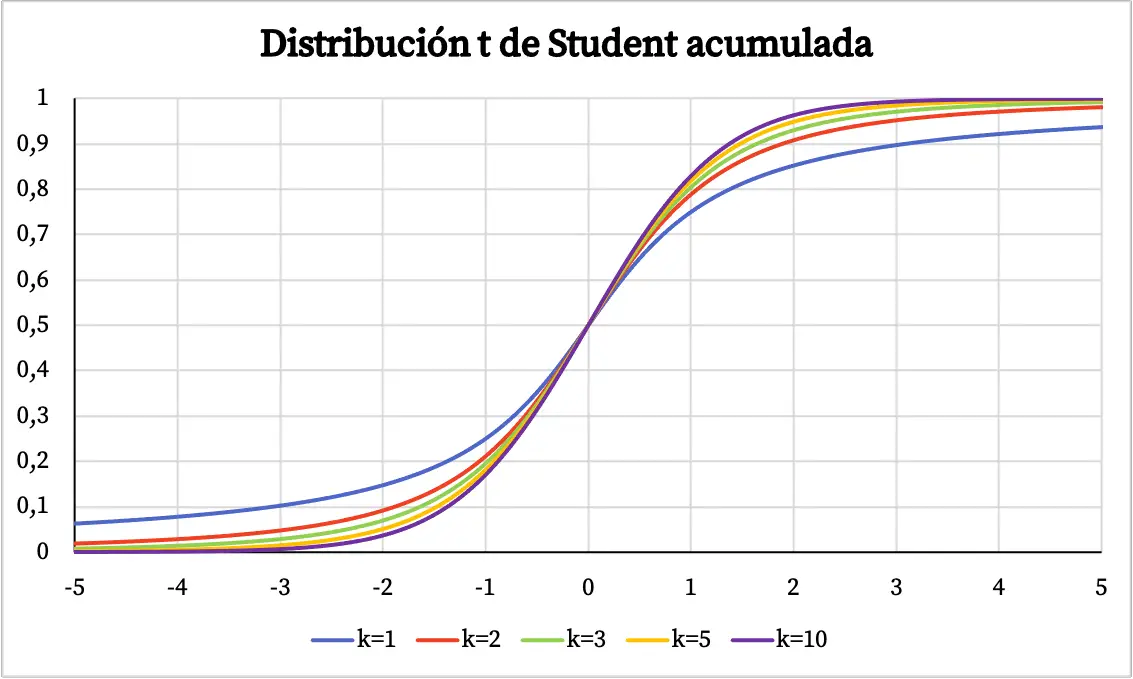
Характеристики распределения Стьюдента
Наиболее важные характеристики распределения Стьюдента показаны ниже.
- Область распределения Стьюдента t состоит из действительных чисел.
![]()
- Для t-распределений Стьюдента с более чем одной степенью свободы среднее значение распределения равно 0.
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} » title=»Rendered by QuickLaTeX.com» height=»55″ width=»190″ style=»vertical-align: 0px;»></p>
</p>
<ul>
<li> Дисперсия распределения Стьюдента может быть рассчитана с использованием следующего выражения:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png)
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} » title=»Rendered by QuickLaTeX.com» height=»75″ width=»245″ style=»vertical-align: 0px;»></p>
</p>
<ul>
<li> Медиана и мода распределения Стьюдента, независимо от количества степеней свободы, всегда равны 0.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png)
- Функция плотности t-распределения Стьюдента определяется следующей формулой:
![]()
- Кумулятивная функция распределения вероятностей t-распределения Стьюдента определяется следующей формулой:
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png)
- Для t-распределений Стьюдента со степенями свободы больше 3 коэффициент асимметрии равен нулю, поскольку это симметричное распределение.
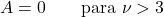
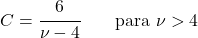 Применение распределения Стьюдента
Применение распределения Стьюдента
Распределение Стьюдента — это распределение вероятностей, широко используемое в статистике. На самом деле существует даже t-критерий Стьюдента, который используется для проверки гипотез и доверительных интервалов.
Таким образом, t-распределение Стьюдента позволяет нам анализировать разницу между средними значениями двух выборок, точнее, оно используется для определения того, имеют ли две выборки существенно разные средние значения. Аналогичным образом, t-критерий Стьюдента используется, чтобы выяснить, имеет ли линия, полученная в результате анализа линейной регрессии, наклон или нет.
Короче говоря, применение t-распределения Стьюдента основано на анализе наборов данных, которые теоретически соответствуют нормальному распределению, но общее количество наблюдений слишком мало, чтобы использовать этот тип распределения.