Распределение хи-квадрат

К бенджамин андерсон 4 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое распределение хи-квадрат и для чего оно используется. Кроме того, вы найдете график распределения хи-квадрат и его свойства.

Что такое распределение хи-квадрат?

Распределение хи-квадрат — это распределение вероятностей, символ которого — χ². Точнее, распределение хи-квадрат представляет собой сумму квадратов k независимых случайных величин с нормальным распределением.

Таким образом, распределение Хи-квадрат имеет k степеней свободы. Следовательно, распределение хи-квадрат имеет столько степеней свободы, сколько сумма квадратов нормально распределенных переменных, которые оно представляет.

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

Распределение Хи-квадрат также известно как распределение Пирсона .

Следует отметить, что распределение Хи-квадрат является частным случаем гамма-распределения.

Распределение хи-квадрат широко используется в статистических выводах, например, при проверке гипотез и доверительных интервалах. Ниже мы увидим, каковы применения этого типа распределения вероятностей.

График распределения хи-квадрат

Как только мы увидим определение распределения Хи-квадрат, мы увидим несколько примеров распределения этого типа, представленных графически. Итак, ниже вы можете увидеть, как вероятностный график распределения хи-квадрат меняется в зависимости от степеней свободы.

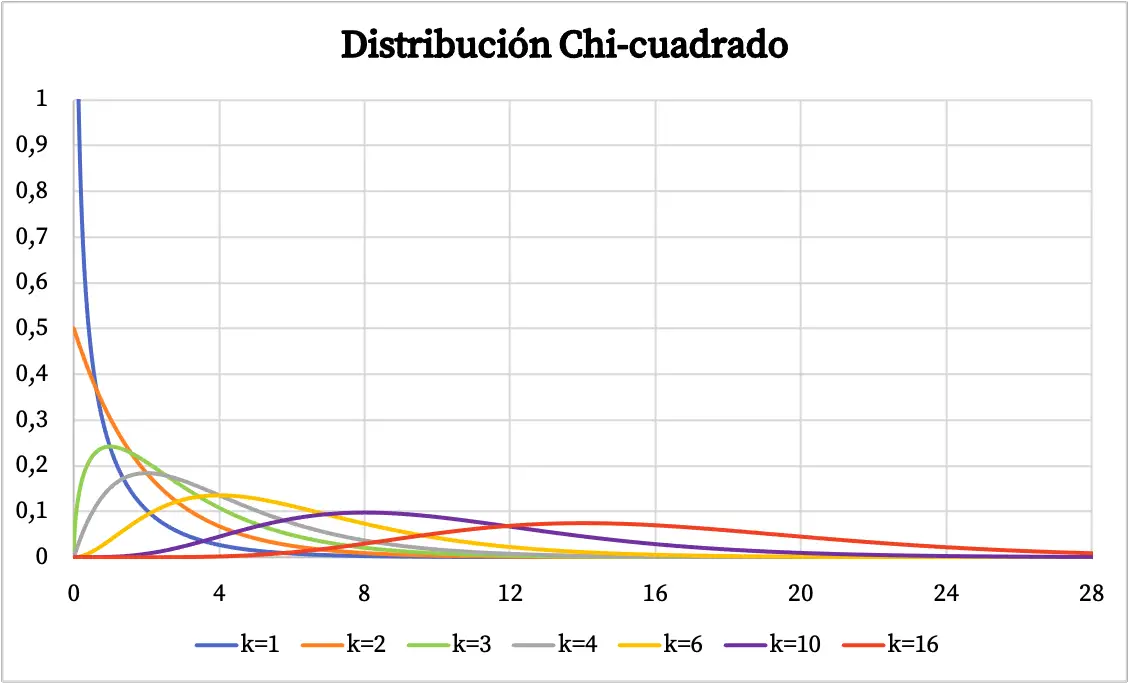
Функция плотности распределения хи-квадрат изображена на графике выше. С другой стороны, график кумулятивной функции распределения вероятностей хи-квадрат выглядит следующим образом:

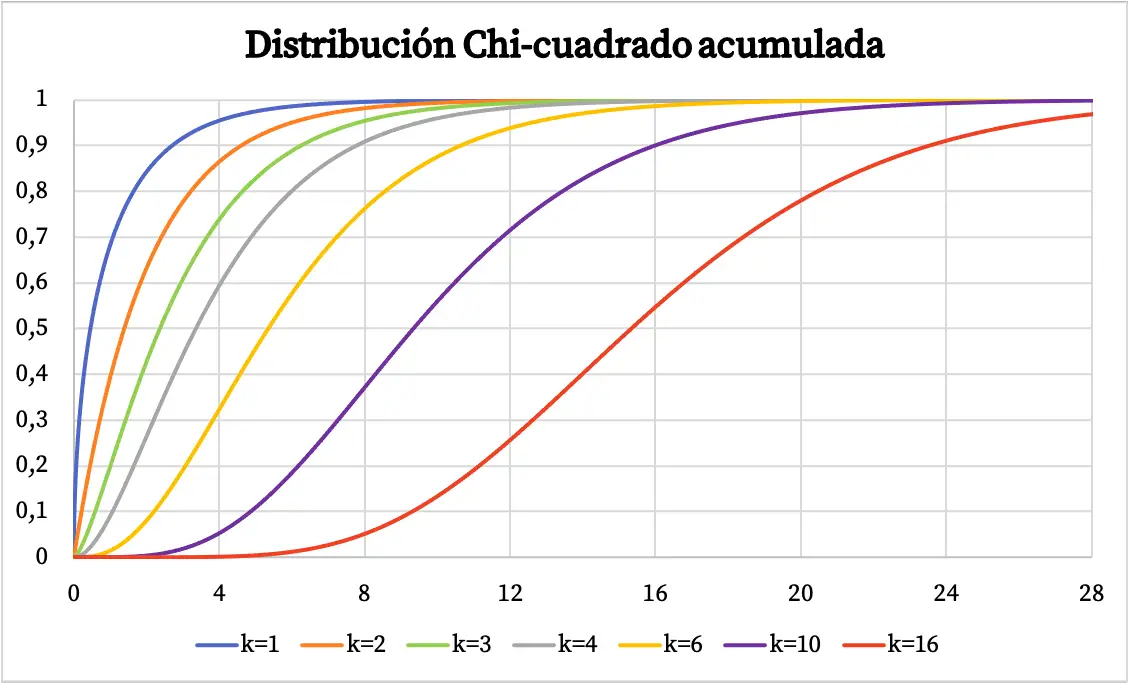
кумулятивный график распределения хи-квадрат

➤ См.: Таблица распределения хи-квадрат.

Характеристики распределения хи-квадрат

В этом разделе мы увидим наиболее важные свойства распределения Хи-квадрат, связанные с теорией вероятностей и статистикой.

Среднее значение распределения хи-квадрат равно его степеням свободы.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

Дисперсия распределения Хи-квадрат равна удвоенной степени свободы распределения.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

Мода распределения хи-квадрат на две единицы меньше его степеней свободы, если распределение имеет более одной степени свободы.

$Mo=k-2 \qquad \text{si } k\geq 2$

Функция плотности распределения Хи-квадрат равна нулю, если x=0. Однако для значений x больше 0 функция плотности распределения хи-квадрат определяется следующей формулой:

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

Кумулятивная функция распределения распределения Хи-квадрат определяется следующей формулой:

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

Коэффициент асимметрии распределения Хи-квадрат представляет собой квадратный корень из частного из восьми, разделенного на количество степеней свободы распределения.

$\displaystyle A=\sqrt{\frac{8}{k}}$

Эксцесс распределения Хи-квадрат рассчитывается с использованием следующего выражения:

$C=3+\cfrac{12}{k}$

Согласно центральной предельной теореме, распределение хи-квадрат можно аппроксимировать нормальным распределением, если k достаточно велико.

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

Применение распределения хи-квадрат

Распределение хи-квадрат имеет множество различных применений в статистике. Фактически, существует даже тест хи-квадрат, который используется для проверки независимости переменных и степени соответствия теоретическому распределению. Например, критерий хи-квадрат можно использовать, чтобы определить, соответствуют ли данные выборки распределению Пуассона.

В анализе линейной регрессии распределение хи-квадрат также используется для оценки среднего значения нормально распределенной совокупности и для оценки наклона линии исследования линейной регрессии.

Наконец, распределение Хи-квадрат также участвует в дисперсионном анализе благодаря своей связи с распределением F Снедекора.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше