Снедекор ф дистрибуция
В этой статье объясняется, что представляет собой дистрибутив Snedecor F и для чего он используется. Кроме того, вы сможете увидеть график распределения Snedecor F и его статистические свойства.
Что представляет собой дистрибутив Snedecor F?
Распределение F Снедекора , также называемое F-распределением Фишера-Снедекора или просто F-распределением , представляет собой непрерывное распределение вероятностей, используемое в статистических выводах, особенно в дисперсионном анализе.
Одним из свойств распределения F Снедекора является то, что оно определяется значением двух действительных параметров m и n , которые указывают их степени свободы. Таким образом, символом распределения F Снедекора является F m,n , где m и n — параметры, определяющие распределение.

![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
Распределение Фишера-Снедекора F обязано своим названием английскому статистику Рональду Фишеру и американскому статистику Джорджу Снедекору.
В статистике распределение Фишера-Снедекора F имеет различные применения. Например, распределение F Фишера-Снедекора используется для сравнения различных моделей линейной регрессии, и это распределение вероятностей используется в дисперсионном анализе (ANOVA).
Схема распределения Snedecor F
Как только мы ознакомились с определением распределения Снедекора F, ниже показаны график его функции плотности и график его кумулятивной вероятности.
На графике ниже вы можете увидеть несколько примеров распределений Snedecor F с разными степенями свободы.
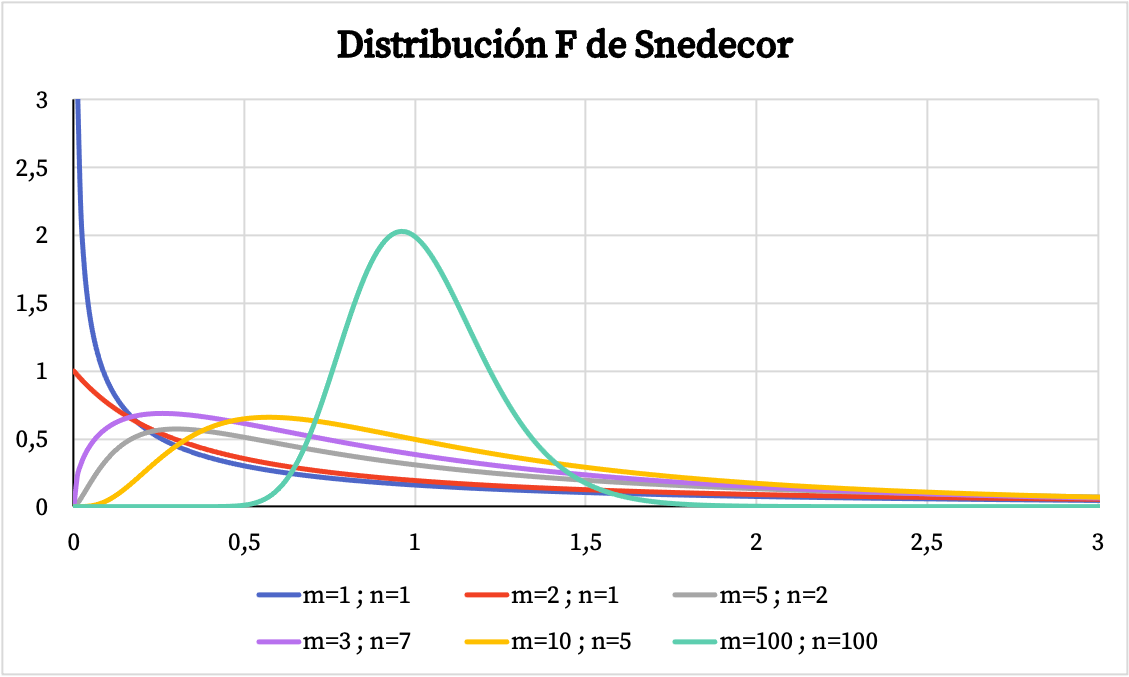
С другой стороны, на графике ниже вы можете видеть, как график кумулятивной функции вероятности распределения Снедекора F меняется в зависимости от его характеристических значений.
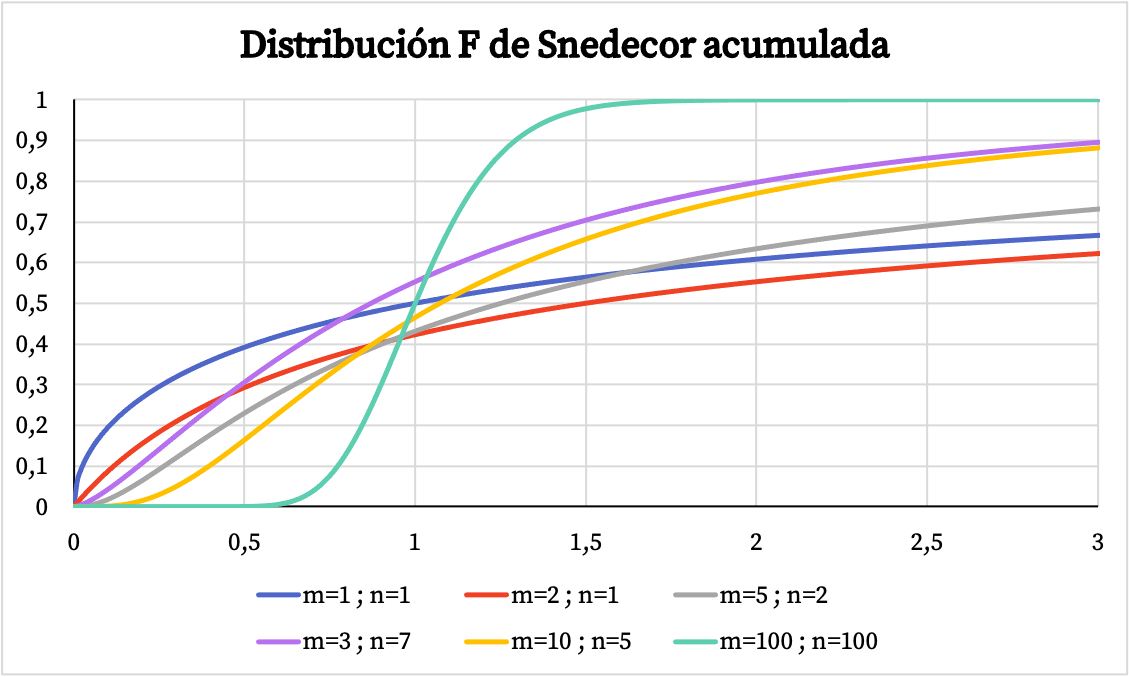
Характеристики распределения Snedecor F
Наконец, в этом разделе представлены наиболее важные характеристики дистрибутива Snedecor F.
- Степени свободы распределения Снедекора F, m и n , являются двумя параметрами, которые определяют форму распределения. Эти характеристические значения распределения Snedecor F являются целыми положительными числами.
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}» title=»Rendered by QuickLaTeX.com» height=»54″ width=»68″ style=»vertical-align: 0px;»></p>
</p>
<ul>
<li> Область распределения Снедекора F состоит из всех действительных чисел, больших или равных нулю.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- Для значений n больше 2 среднее значение распределения Снедекора F равно n при вычитании n минус 2.
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} » title=»Rendered by QuickLaTeX.com» height=»75″ width=»225″ style=»vertical-align: 0px;»></p>
</p>
<ul>
<li> Когда параметр <em>n</em> больше 2, дисперсию распределения Снедекора F можно рассчитать, применив следующую формулу:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} » title=»Rendered by QuickLaTeX.com» height=»80″ width=»366″ style=»vertical-align: 0px;»></p>
</p>
<ul>
<li> Если параметр <em>m</em> больше 2, режим распределения Снедекора F можно рассчитать с помощью следующего выражения:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
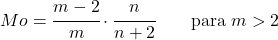
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- Если переменная соответствует распределению Снедекора F со степенями свободы m и n , то обратная указанная переменная соответствует распределению Снедекора F с теми же степенями свободы, но с изменением порядка ее значений.
![]()
- Распределение Стьюдента имеет следующую связь с распределением Snedecor F:
![]()