Регрессия главных компонентов в python (шаг за шагом)
Учитывая набор переменных-предикторов p и переменную отклика, множественная линейная регрессия использует метод, известный как наименьшие квадраты, для минимизации остаточной суммы квадратов (RSS):
RSS = Σ(y i – ŷ i ) 2
Золото:
- Σ : греческий символ, означающий сумму.
- y i : фактическое значение ответа для i-го наблюдения
- ŷ i : прогнозируемое значение ответа на основе модели множественной линейной регрессии.
Однако, когда переменные-предикторы сильно коррелируют, мультиколлинеарность может стать проблемой. Это может сделать оценки коэффициентов модели ненадежными и привести к высокой дисперсии.
Один из способов избежать этой проблемы — использовать регрессию главных компонентов , которая находит M линейных комбинаций (называемых «главными компонентами») исходных p- предикторов, а затем использует метод наименьших квадратов для соответствия модели линейной регрессии, используя главные компоненты в качестве предикторов.
В этом руководстве представлен пошаговый пример выполнения регрессии главных компонентов в Python.
Шаг 1. Импортируйте необходимые пакеты.
Сначала мы импортируем пакеты, необходимые для выполнения регрессии главных компонентов (PCR) в Python:
import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn. PCA import decomposition
from sklearn. linear_model import LinearRegression
from sklearn. metrics import mean_squared_error
Шаг 2. Загрузите данные
В этом примере мы будем использовать набор данных mtcars , который содержит информацию о 33 различных автомобилях. Мы будем использовать hp в качестве переменной ответа и следующие переменные в качестве предикторов:
- миль на галлон
- отображать
- дерьмо
- масса
- qsec
Следующий код показывает, как загрузить и отобразить этот набор данных:
#define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"
#read in data
data_full = pd. read_csv (url)
#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]
#view first six rows of data
data[0:6]
mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105
Шаг 3. Настройте модель ПЦР
Следующий код показывает, как подогнать модель PCR к этим данным. Обратите внимание на следующее:
- pca.fit_transform(scale(X)) : это сообщает Python, что каждая из переменных-предикторов должна быть масштабирована так, чтобы иметь среднее значение 0 и стандартное отклонение 1. Это гарантирует, что ни одна переменная-предиктор не будет иметь слишком большого влияния на модель, если это происходит. измерять в разных единицах.
- cv = RepeatedKFold() : это говорит Python использовать перекрестную проверку в k-кратном размере для оценки производительности модели. Для этого примера мы выбираем k = 10 складок, повторяем 3 раза.
#define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]
#scale predictor variables
pca = pca()
X_reduced = pca. fit_transform ( scale (X))
#define cross validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )
regr = LinearRegression()
mse = []
# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (regr,
n.p. ones ((len(X_reduced),1)), y, cv=cv,
scoring=' neg_mean_squared_error '). mean ()
mse. append (score)
# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
score = -1*model_selection. cross_val_score (regr,
X_reduced[:,:i], y, cv=cv, scoring=' neg_mean_squared_error '). mean ()
mse. append (score)
# Plot cross-validation results
plt. plot (mse)
plt. xlabel ('Number of Principal Components')
plt. ylabel ('MSE')
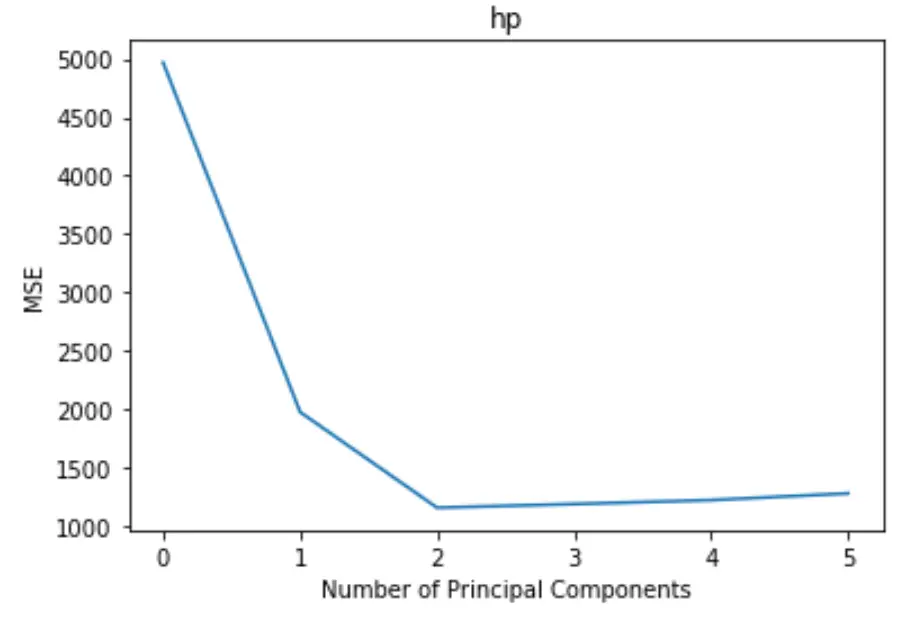
plt. title ('hp')
На графике отображается количество главных компонентов по оси X и тест MSE (среднеквадратическая ошибка) по оси Y.
На графике мы видим, что MSE теста уменьшается при добавлении двух главных компонентов, но начинает увеличиваться, когда мы добавляем более двух главных компонентов.
Таким образом, оптимальная модель включает только первые две главные компоненты.
Мы также можем использовать следующий код для расчета процента дисперсии переменной ответа, объясняемой путем добавления каждого основного компонента в модель:
n.p. cumsum (np. round (pca. explained_variance_ratio_ , decimals= 4 )* 100 )
array([69.83, 89.35, 95.88, 98.95, 99.99])
Мы можем увидеть следующее:
- Используя только первый главный компонент, мы можем объяснить 69,83% вариаций переменной отклика.
- Добавляя второй главный компонент, мы можем объяснить 89,35% вариаций переменной отклика.
Обратите внимание, что мы по-прежнему сможем объяснить большую дисперсию, используя больше главных компонентов, но мы видим, что добавление более двух главных компонентов на самом деле не сильно увеличивает процент объясненной дисперсии.
Шаг 4. Используйте окончательную модель для прогнозирования
Мы можем использовать окончательную двухглавную модель ПЦР для прогнозирования новых наблюдений.
Следующий код показывает, как разделить исходный набор данных на обучающий и тестовый набор и использовать модель PCR с двумя основными компонентами для прогнозирования тестового набора.
#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size= 0.3 , random_state= 0 )
#scale the training and testing data
X_reduced_train = pca. fit_transform ( scale (X_train))
X_reduced_test = pca. transform ( scale (X_test))[:,:1]
#train PCR model on training data
regr = LinearRegression()
reg. fit (X_reduced_train[:,:1], y_train)
#calculate RMSE
pred = regr. predict (X_reduced_test)
n.p. sqrt ( mean_squared_error (y_test, pred))
40.2096
Мы видим, что тест RMSE оказывается равным 40.2096 . Это среднее отклонение между прогнозируемым значением hp и наблюдаемым значением hp для наблюдений тестового набора.
Полный код Python, использованный в этом примере, можно найти здесь .