Что такое сбалансированная точность? (определение & #038; пример)

Сбалансированная точность — это показатель, который мы можем использовать для оценки производительности модели классификации .

Он рассчитывается следующим образом:

Сбалансированная точность = (Чувствительность + Специфичность) / 2

Золото:

• Чувствительность : «истинно положительный показатель» — процент положительных случаев, которые модель способна обнаружить.
• Специфичность : «истинно отрицательный показатель» — процент отрицательных случаев, которые модель способна обнаружить.

Этот показатель особенно полезен, когда два класса несбалансированы, то есть один класс появляется намного больше, чем другой.

В следующем примере показано, как на практике рассчитать сбалансированную точность, и показано, почему это такой полезный показатель.

Пример: расчет сбалансированной точности

Предположим, спортивный аналитик использует модель логистической регрессии , чтобы спрогнозировать, будут ли 400 баскетболистов из разных колледжей выбраны в НБА.

Следующая матрица путаницы суммирует прогнозы, сделанные моделью:

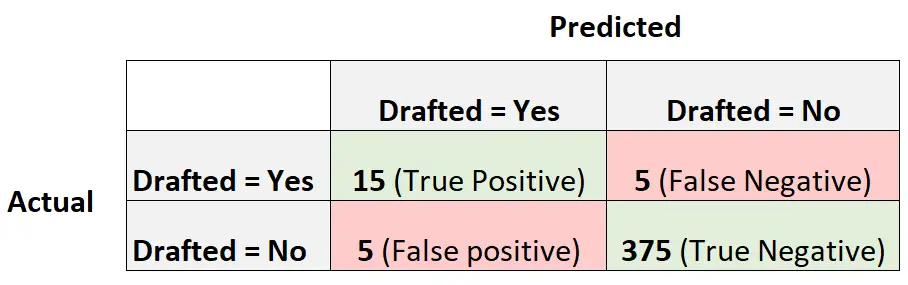
Чтобы рассчитать сбалансированную точность модели, мы сначала рассчитаем чувствительность и специфичность:

• Чувствительность : «истинно положительный уровень» = 15 / (15 + 5) = 0,75.
• Специфичность : «истинно отрицательный коэффициент» = 375 / (375 + 5) = 0,9868.

Затем мы можем рассчитать сбалансированную точность следующим образом:

• Сбалансированная точность = (Чувствительность + Специфичность) / 2
• Сбалансированная точность = (0,75 + 9868)/2
• Сбалансированная точность = 0,8684

Сбалансированная точность модели оказывается равной 0,8684 .

Обратите внимание: чем ближе сбалансированная точность к 1, тем лучше модель способна правильно классифицировать наблюдения.

В этом примере сбалансированная точность довольно высока, что говорит нам о том, что модель логистической регрессии очень хорошо прогнозирует, будут ли игроки колледжа призваны в НБА.

В этом сценарии, поскольку классы очень несбалансированы (20 игроков были выбраны, а 380 игроков — нет), сбалансированная точность дает нам более реалистичную картину производительности модели по сравнению с общим показателем точности.

Например, мы могли бы рассчитать точность модели следующим образом:

• Точность = (TP + TN) / (TP + TN + FP + FN)
• Точность = (15 + 375) / (15 + 375 + 5 + 5)
• Точность = 0,975

Точность модели составляет 0,975 , что кажется чрезвычайно высоким.

Однако рассмотрим модель, которая просто предсказывает, что каждый игрок останется незадрафтованным. Точность будет 380/400 = 0,95 . Это лишь немного ниже точности нашей модели.

Сбалансированный показатель точности 0,8684 дает нам лучшее представление о способности модели прогнозировать оба класса.

Другими словами, это дает нам лучшее представление о способности модели предсказывать, какие игроки останутся незадрафтованными , а какие останутся.

Дополнительные ресурсы

В следующих руководствах объясняется, как создать матрицу путаницы в различных статистических программах:

Как создать матрицу путаницы в Excel
Как создать матрицу путаницы в R
Как создать матрицу путаницы в Python