Что такое случайные величины?

Случайная переменная , обычно обозначаемая X, — это переменная, возможные значения которой являются результатом случайного процесса.

Существует два типа случайных величин: дискретные и непрерывные .

Дискретные случайные величины

Дискретная случайная величина — это такая величина, которая может принимать только счетное количество различных значений, например 0, 1, 2, 3, 4, 5…100, 1 миллион и т. д. Вот несколько примеров дискретных случайных величин:

• Сколько раз монета выпала решкой после того, как ее подбросили 20 раз.
• Сколько раз на кубике выпадает цифра 4 после 100 бросков.
• Количество бракованных виджетов в коробке 50 виджетов.

Распределение вероятностей дискретной случайной величины говорит нам о вероятности того, что случайная величина примет определенные значения.

Например, предположим, что мы один раз бросаем честную игральную кость. Если мы обозначим X вероятность того, что на игральной кости выпадет определенное число, то распределение вероятностей можно записать следующим образом:

• Р(Х=1): 1/6
• Р(Х=2): 1/6
• Р(Х=3): 1/6
• Р(Х=4): 1/6
• Р(Х=5): 1/6
• Р(Х=6): 1/6

Примечание:

Чтобы распределение вероятностей было действительным, оно должно удовлетворять следующим двум критериям:

1. Вероятность каждого исхода должна находиться в диапазоне от 0 до 1.

2. Сумма всех вероятностей должна составлять 1.

Обратите внимание, что распределение вероятностей для броска игральной кости удовлетворяет обоим этим критериям:

1. Вероятность каждого исхода находится в диапазоне от 0 до 1.

2. Сумма всех вероятностей равна 1.

Мы можем использовать гистограмму для визуализации распределения вероятностей:

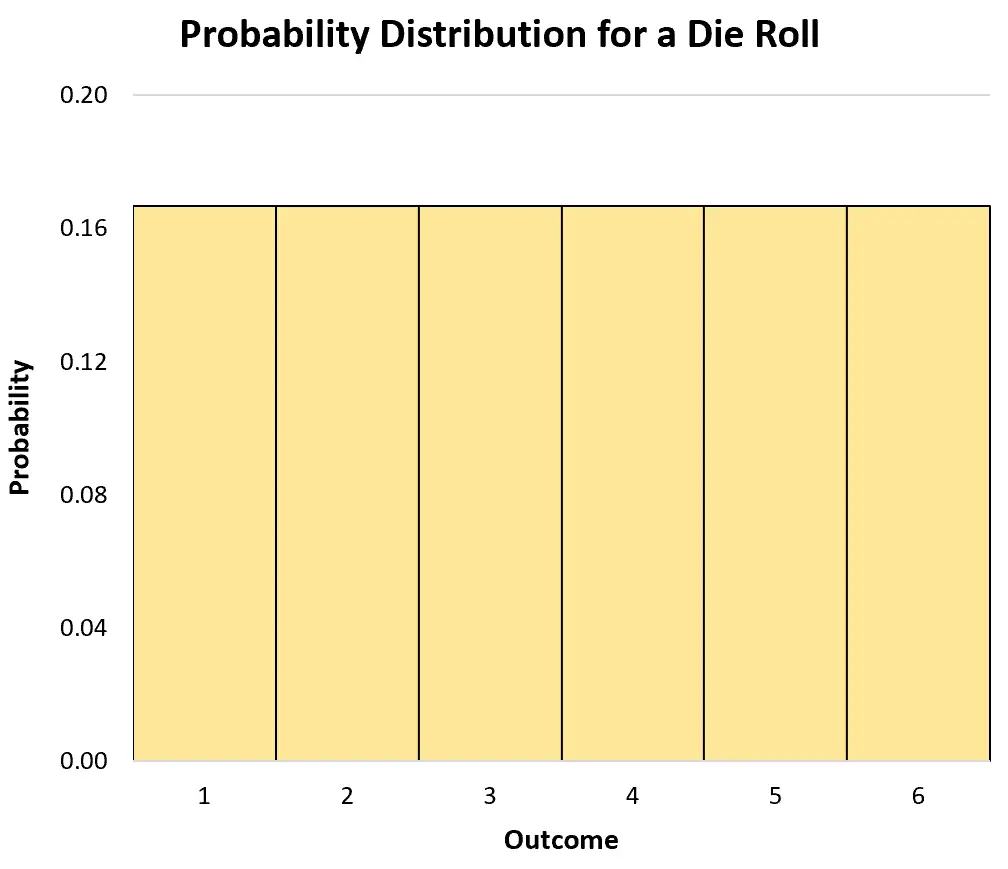
Кумулятивное распределение вероятностей для дискретной случайной величины показывает нам вероятность того, что переменная примет значение , равное или меньше определенного значения.

Например, совокупное распределение вероятностей для броска кубика будет выглядеть так:

• Р(Х≤1): 1/6
• Р(Х≤2): 2/6
• Р(Х≤3): 3/6
• Р(Х<4): 4/6
• Р(Х<5): 5/6
• Р(Х≤6): 6/6

Вероятность того, что на кубике выпадет одно или меньшее число, равна просто 1/6, поскольку на кубике не может выпасть число меньше единицы.

Вероятность того, что он приземлится на двоих или меньше, равна P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6.

Аналогично, вероятность того, что выпадет три или меньше очков, равна P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6, и скоро.

Мы также можем использовать гистограмму для визуализации кумулятивного распределения вероятностей:

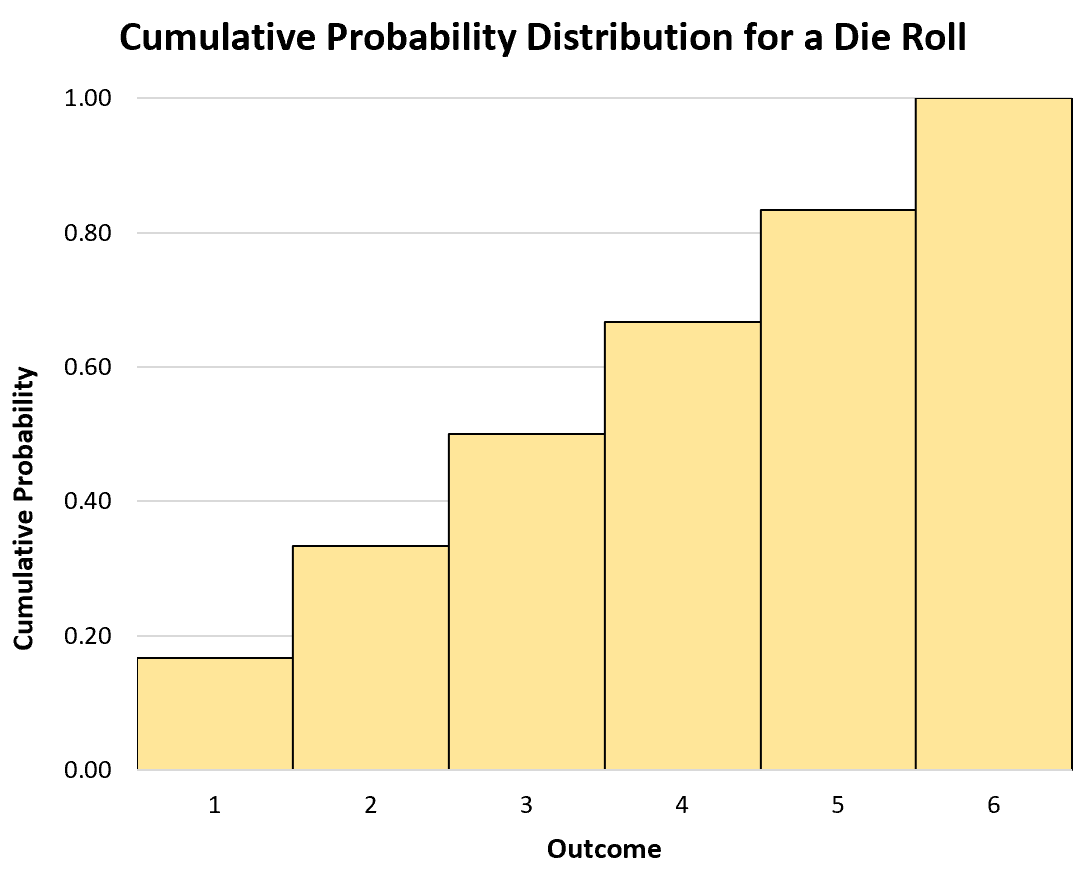
Непрерывные случайные величины

Непрерывная случайная величина — это переменная, которая может принимать бесконечное множество возможных значений. Вот несколько примеров непрерывных случайных величин:

• Вес животного
• Рост человека
• Время, необходимое для пробежки марафона

Например, рост человека может составлять 60,2 дюйма, 65,2344 дюйма, 70,431222 дюйма и т. д. Существует бесконечное количество возможных значений размера.

Главное правило:

Если вы можете подсчитать количество исходов, то вы работаете с дискретной случайной величиной — например, подсчитываете, сколько раз монета выпала орлом.

Но если вы можете измерить результат, вы работаете с непрерывной случайной величиной — например, измеряете рост, вес, время и т. д.

Распределение вероятностей для непрерывной случайной величины говорит нам о вероятности того, что случайная величина примет определенные значения.

Однако, в отличие от распределения вероятностей для дискретных случайных величин, распределение вероятностей для непрерывной случайной величины можно использовать только для того, чтобы сообщить нам вероятность того, что переменная принимает диапазон значений.

Например, предположим, что мы хотим узнать вероятность того, что гамбургер из определенного ресторана весит четверть фунта (0,25 фунта). Поскольку вес является непрерывной переменной, он может принимать бесконечное количество значений.

Например, данный гамбургер может фактически весить 0,250001 фунта, или 0,24 фунта, или 0,2488 фунта. Вероятность того, что данный гамбургер будет весить ровно 0,25 фунта, практически равна нулю.

Таким образом, мы можем использовать распределение вероятностей только для того, чтобы определить вероятность того, что гамбургер весит менее 0,25 фунта, более 0,25 фунта или находится в определенном диапазоне (например, от 0,23 фунта до 0,27 фунта).

Дополнительные ресурсы

Следующие руководства предоставляют дополнительную информацию о случайных величинах:

Что такое случайные переменные iid?
10 примеров случайных величин в реальной жизни