Как создать нормальное распределение в python (с примерами)
Вы можете быстро сгенерировать нормальное распределение в Python, используя функцию numpy.random.normal() , которая использует следующий синтаксис:
numpy. random . normal (loc=0.0, scale=1.0, size=None)
Золото:
- loc: Среднее распределение. Значение по умолчанию — 0.
- масштаб: стандартное отклонение распределения. Значение по умолчанию — 1.
- размер: размер выборки.
В этом руководстве показан пример использования этой функции для создания нормального распределения в Python.
Связанный: Как создать колоколообразную кривую в Python
Пример: создание нормального распределения в Python
Следующий код показывает, как создать нормальное распределение в Python:
from numpy. random import seed
from numpy. random import normal
#make this example reproducible
seed(1)
#generate sample of 200 values that follow a normal distribution
data = normal (loc=0, scale=1, size=200)
#view first six values
data[0:5]
array([ 1.62434536, -0.61175641, -0.52817175, -1.07296862, 0.86540763])
Мы можем быстро найти среднее и стандартное отклонение этого распределения:
import numpy as np
#find mean of sample
n.p. mean (data)
0.1066888148479486
#find standard deviation of sample
n.p. std (data, ddof= 1 )
0.9123296653173484
Мы также можем создать быструю гистограмму для визуализации распределения значений данных:
import matplotlib. pyplot as plt
count, bins, ignored = plt. hist (data, 30)
plt. show ()
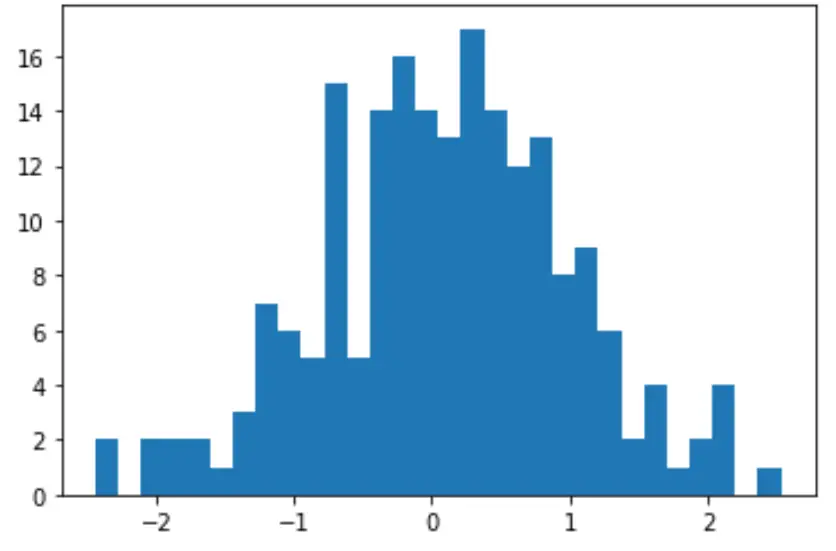
Мы даже можем выполнить тест Шапиро-Уилка, чтобы проверить, получен ли набор данных из нормальной популяции:
from scipy. stats import shapiro
#perform Shapiro-Wilk test
shapiro(data)
ShapiroResult(statistic=0.9958659410, pvalue=0.8669294714)
P-значение теста оказывается равным 0,8669 . Поскольку это значение не меньше 0,05, можно предположить, что данные выборки взяты из нормально распределенной совокупности.
Этот результат не должен вызывать удивления, поскольку мы сгенерировали данные с помощью функции numpy.random.normal() , которая генерирует случайную выборку данных из нормального распределения.