Что такое стандартизированные остатки?

Остаток — это разница между наблюдаемым значением и прогнозируемым значением в регрессионной модели .

Он рассчитывается следующим образом:

Остаток = Наблюдаемое значение – Прогнозируемое значение

Если мы построим наблюдаемые значения и наложим подобранную линию регрессии, остатки для каждого наблюдения будут представлять собой расстояние по вертикали между наблюдением и линией регрессии:

Один тип остатка, который мы часто используем для выявления выбросов в регрессионной модели, называется стандартизированным остатком .

Он рассчитывается следующим образом:

р _я знак равно е _я / s(е _я ) знак равно е _я / RSE√ 1-h _ii

Золото:

• e _i : i- ^й остаток
• RSE: остаточная стандартная ошибка модели.
• h _ii : Рост ^i-го наблюдения

На практике мы часто рассматриваем любой стандартизированный остаток, абсолютное значение которого превышает 3, как выброс.

Это не обязательно означает, что мы удалим эти наблюдения из модели, но нам следует, по крайней мере, изучить их дальше, чтобы убедиться, что они не являются результатом ошибки ввода данных или какого-то другого странного события.

Примечание. Иногда стандартизированные остатки также называют «остатками, изученными собственными силами».

Пример: Как рассчитать стандартизированные остатки

Предположим, у нас есть следующий набор данных с 12 наблюдениями:

Если мы используем статистическое программное обеспечение (например, R , Excel , Python , Stata и т. д.), чтобы подогнать линию линейной регрессии к этому набору данных, мы обнаружим, что линия наилучшего соответствия окажется такой:

у = 29,63 + 0,7553x

Используя эту строку, мы можем вычислить прогнозируемое значение для каждого значения Y на основе значения X. Например, прогнозируемое значение первого наблюдения будет:

у = 29,63 + 0,7553*(8) = 35,67

Затем мы можем вычислить невязку для этого наблюдения следующим образом:

Остаток = Наблюдаемое значение – Прогнозируемое значение = 41 – 35,67 = 5,33

Мы можем повторить этот процесс, чтобы найти остаток для каждого наблюдения:

Мы также можем использовать статистическое программное обеспечение, чтобы определить, что остаточная стандартная ошибка модели равна 4,44 .

И хотя это выходит за рамки данного руководства, мы можем использовать программное обеспечение, чтобы найти статистику рычага (h _ii ) для каждого наблюдения:

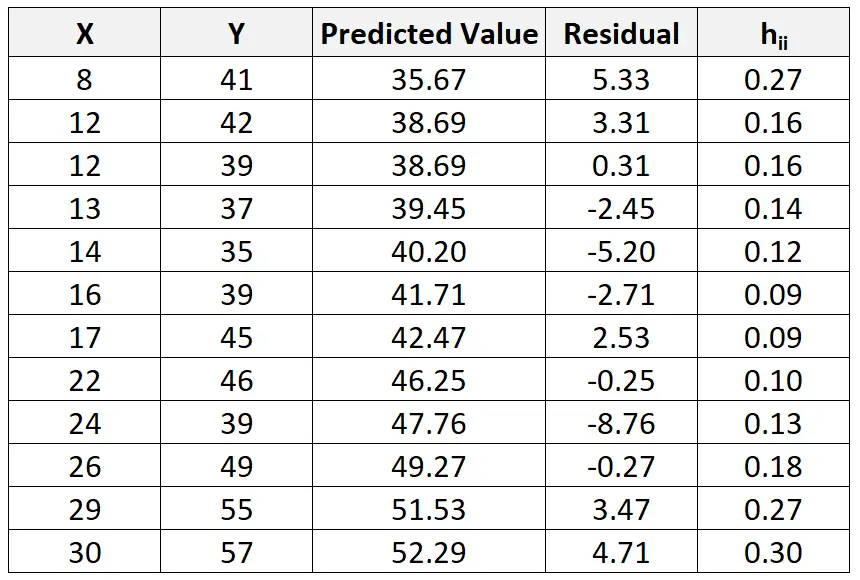
Затем мы можем использовать следующую формулу для расчета стандартизированной невязки для каждого наблюдения:

р _я знак равно е _я / RSE√ 1-h _ii

Например, стандартизированная невязка для первого наблюдения рассчитывается следующим образом:

r _i = 5,33/4,44√ 1-0,27 = 1,404

Мы можем повторить этот процесс, чтобы найти стандартизированную невязку для каждого наблюдения:

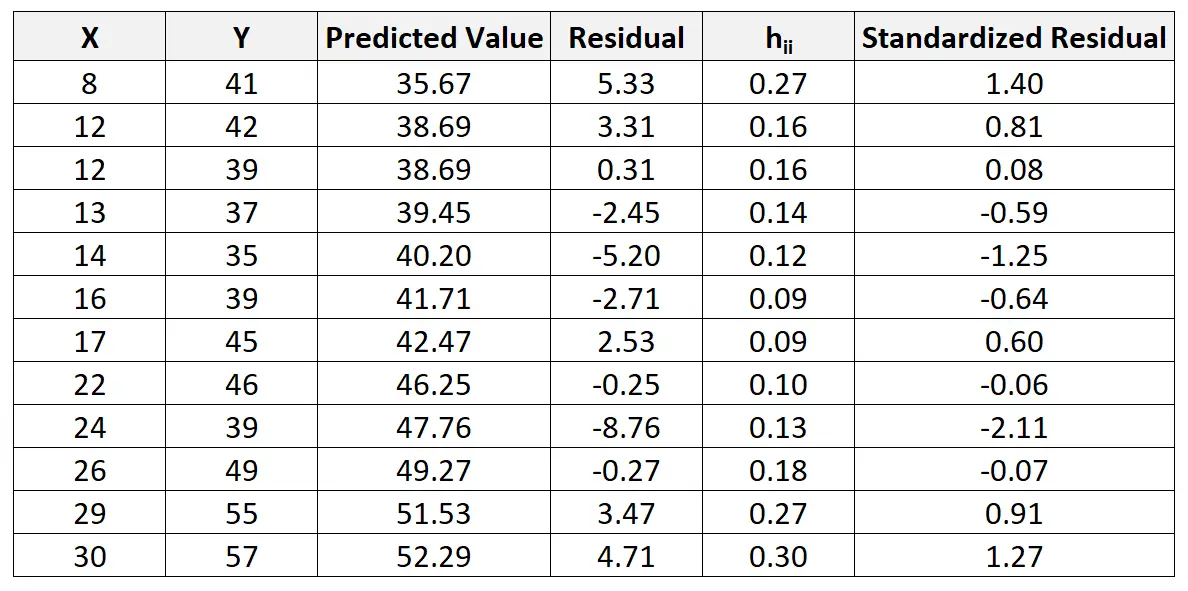
Затем мы можем создать быструю диаграмму рассеяния прогнозируемых значений в сравнении со стандартизированными остатками, чтобы визуально увидеть, превышает ли какой-либо из стандартизированных остатков порог абсолютного значения, равный 3:

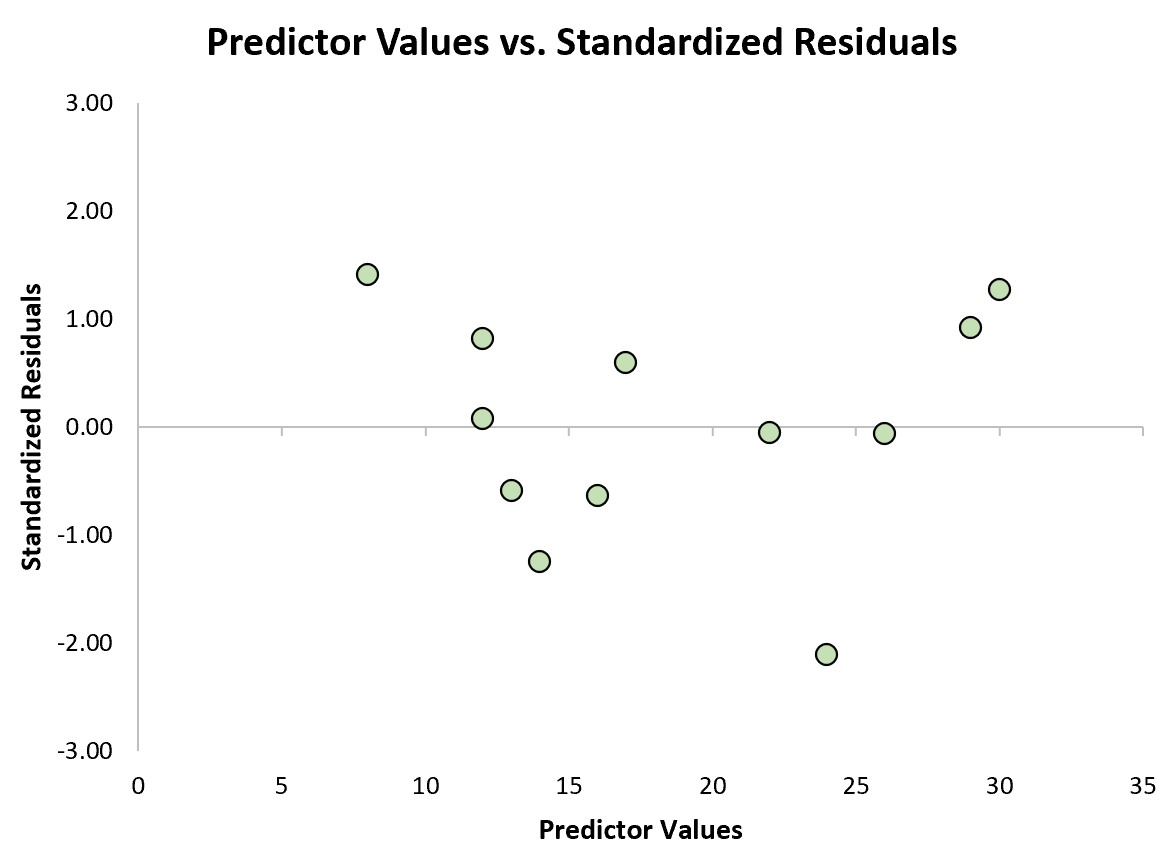
Из графика мы видим, что ни один из стандартизированных остатков не превышает абсолютного значения 3. Таким образом, ни одно из наблюдений не является выбросом.

Следует отметить, что в некоторых случаях исследователи считают выбросами наблюдения, стандартизированные остатки которых превышают абсолютное значение 2.

Вам решать, хотите ли вы использовать абсолютное значение 2 или 3 в качестве порога для выбросов, в зависимости от области, в которой вы работаете, и конкретной проблемы, над которой вы работаете.

Дополнительные ресурсы

Следующие учебные пособия предоставляют дополнительную информацию о стандартизированных остатках:

Что такое остатки в статистике?
Как рассчитать стандартизованные остатки в Excel
Как рассчитать стандартизированные остатки в R
Как вычислить стандартизованные остатки в Python