Какова стандартная ошибка оценки? (определение & #038; пример)
Стандартная ошибка оценки — это способ измерения точности прогнозов, сделанных с помощью регрессионной модели.
Часто отмечают σ est , он рассчитывается следующим образом:
σ = √ Σ(y – ŷ) 2 /n
Золото:
- y: наблюдаемое значение
- ŷ: прогнозируемое значение
- n: Общее количество наблюдений
Стандартная ошибка оценки дает нам представление о том, насколько хорошо модель регрессии соответствует набору данных. Особенно:
- Чем меньше значение, тем лучше соответствие.
- Чем больше значение, тем хуже соответствие.
Для модели регрессии с небольшой стандартной ошибкой оценки точки данных будут плотно сгруппированы вокруг предполагаемой линии регрессии:
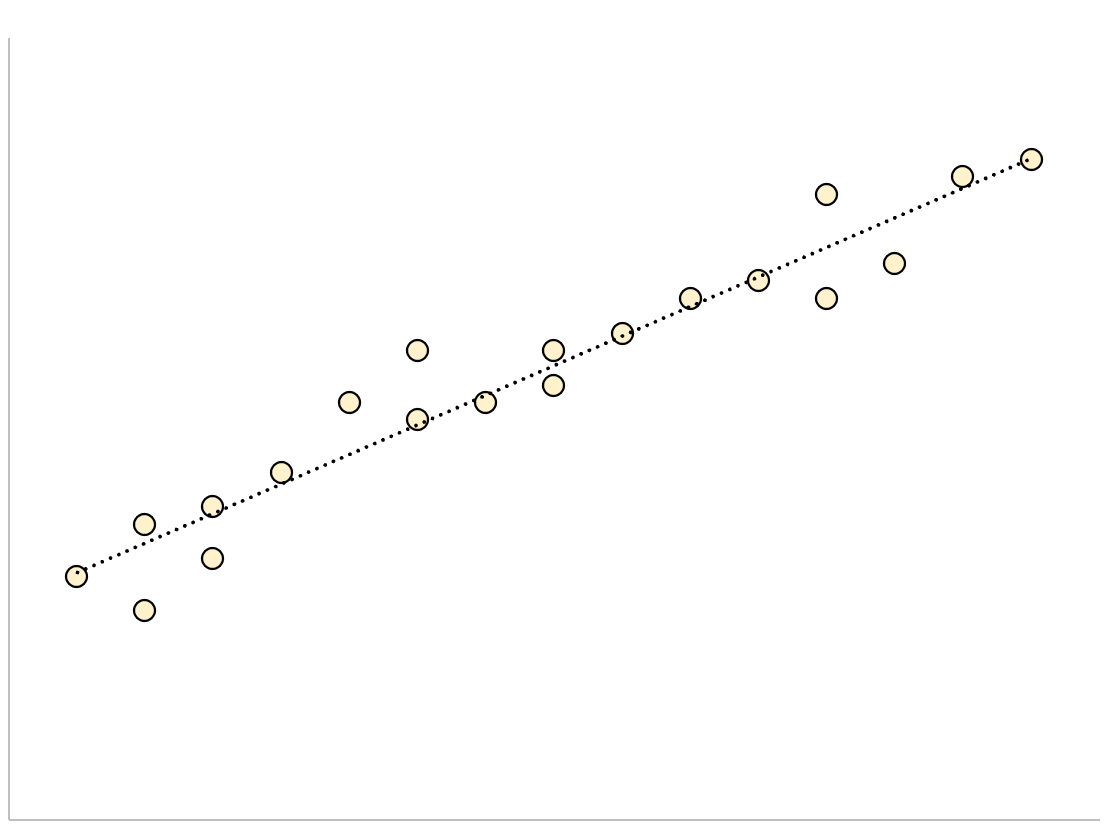
И наоборот, для модели регрессии с большой стандартной ошибкой оценки точки данных будут более свободно разбросаны по линии регрессии:
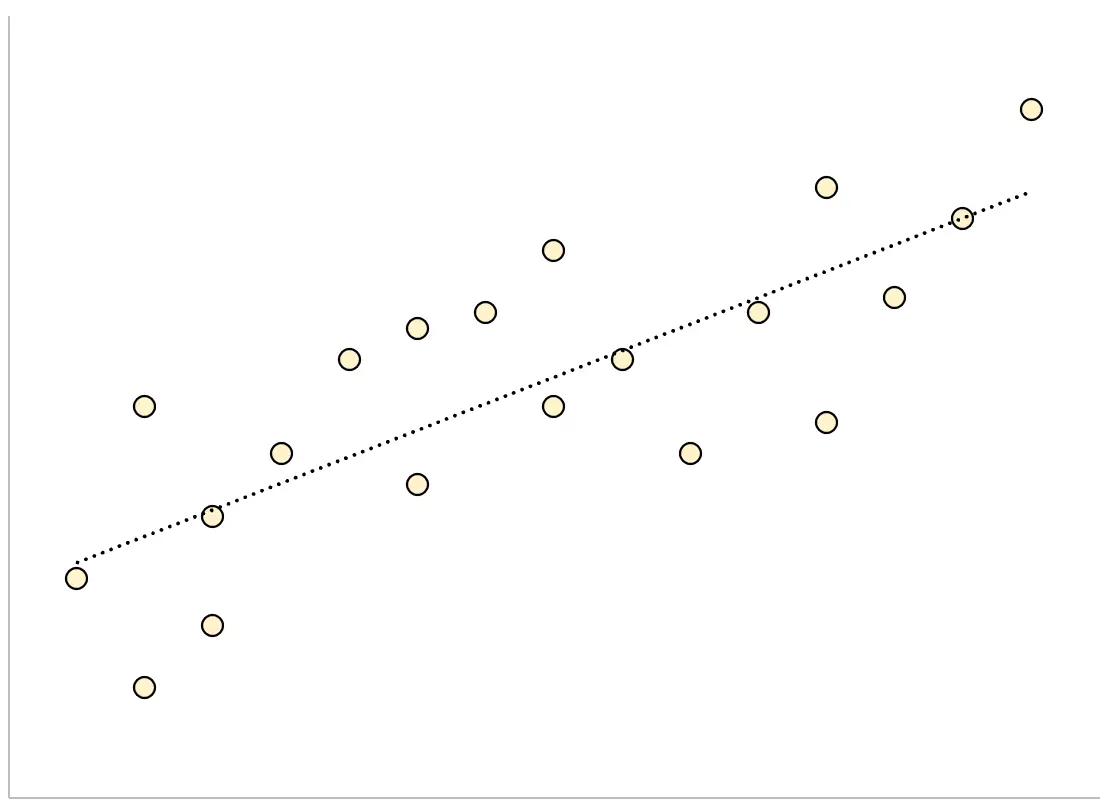
В следующем примере показано, как вычислить и интерпретировать стандартную ошибку оценки для регрессионной модели в Excel.
Пример: стандартная ошибка оценки в Excel
Используйте следующие шаги, чтобы вычислить стандартную ошибку оценки для модели регрессии в Excel.
Шаг 1: Введите данные
Сначала введите значения набора данных:
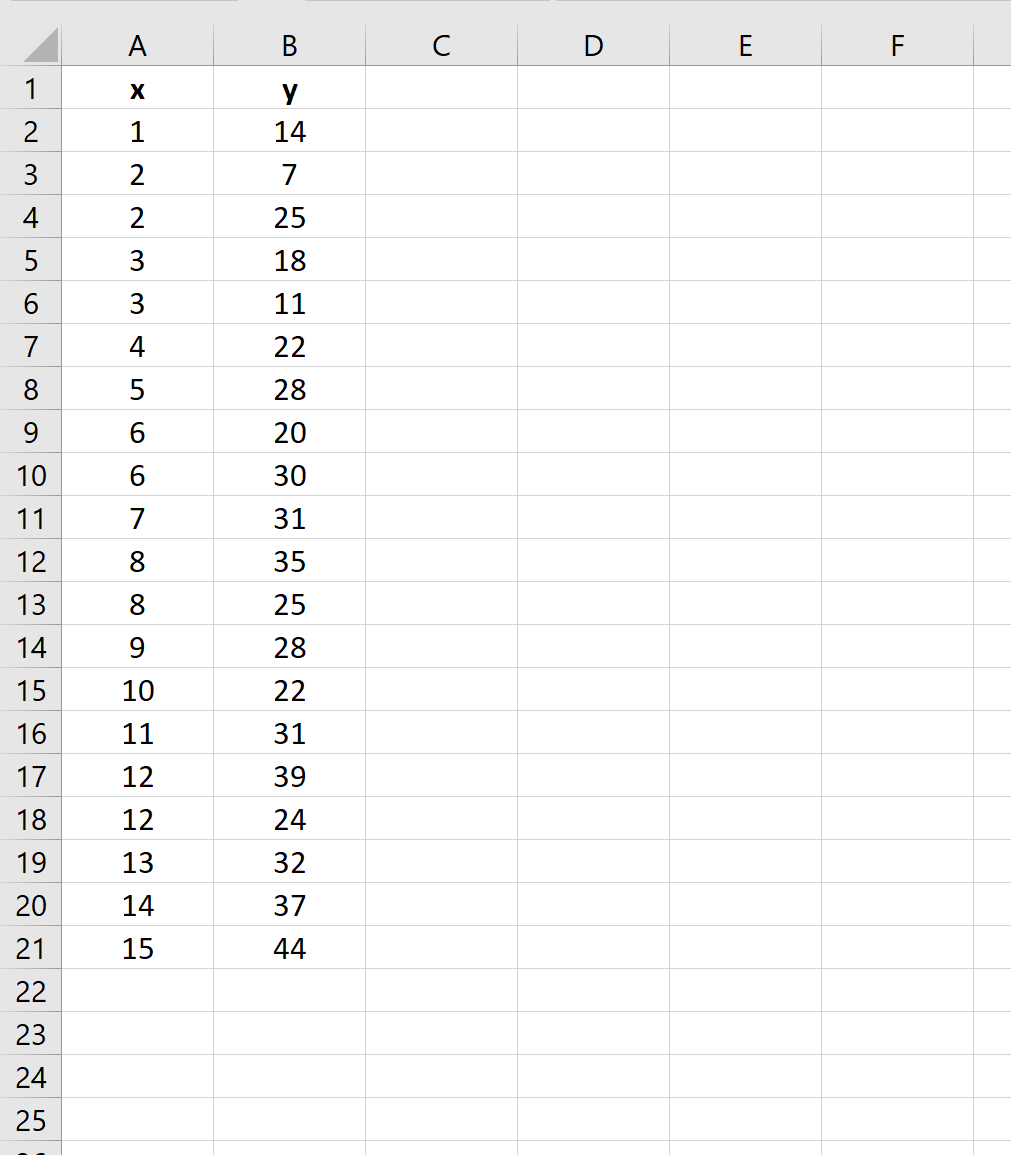
Шаг 2. Выполните линейную регрессию
Затем нажмите вкладку «Данные» на верхней ленте. Затем нажмите кнопку «Анализ данных » в группе «Анализ» .

Если вы не видите эту опцию, вам необходимо сначала загрузить Analysis ToolPak .
В появившемся новом окне нажмите «Регрессия» , а затем нажмите «ОК» .
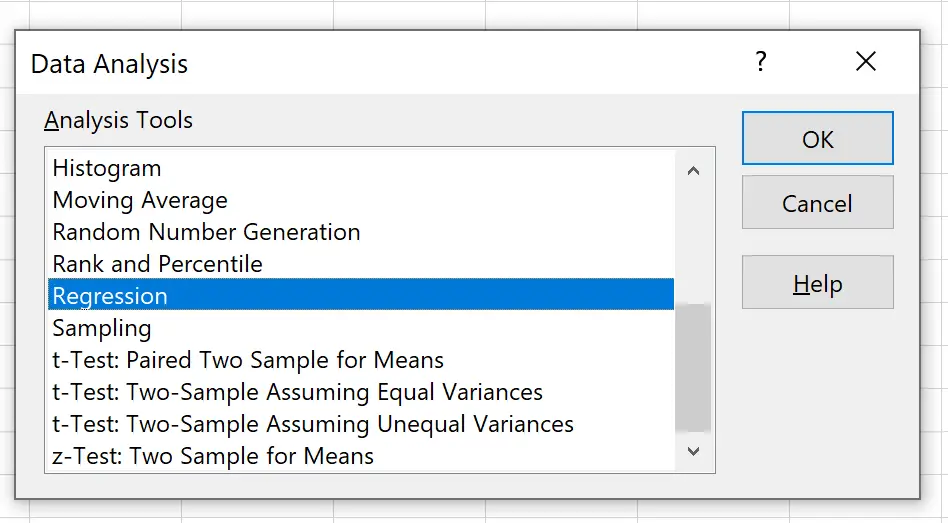
В появившемся новом окне укажите следующую информацию:
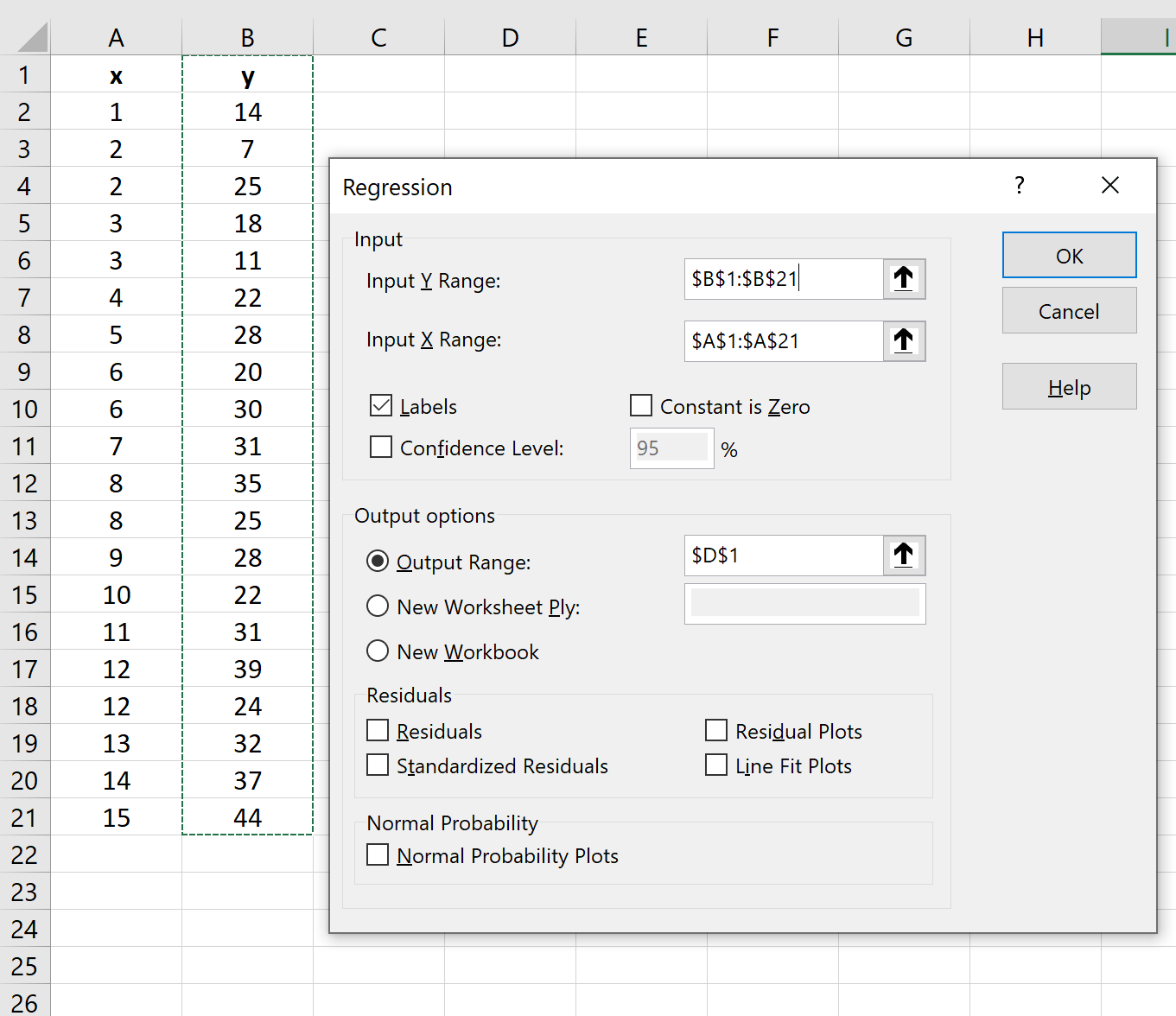
Как только вы нажмете «ОК» , появится результат регрессии:
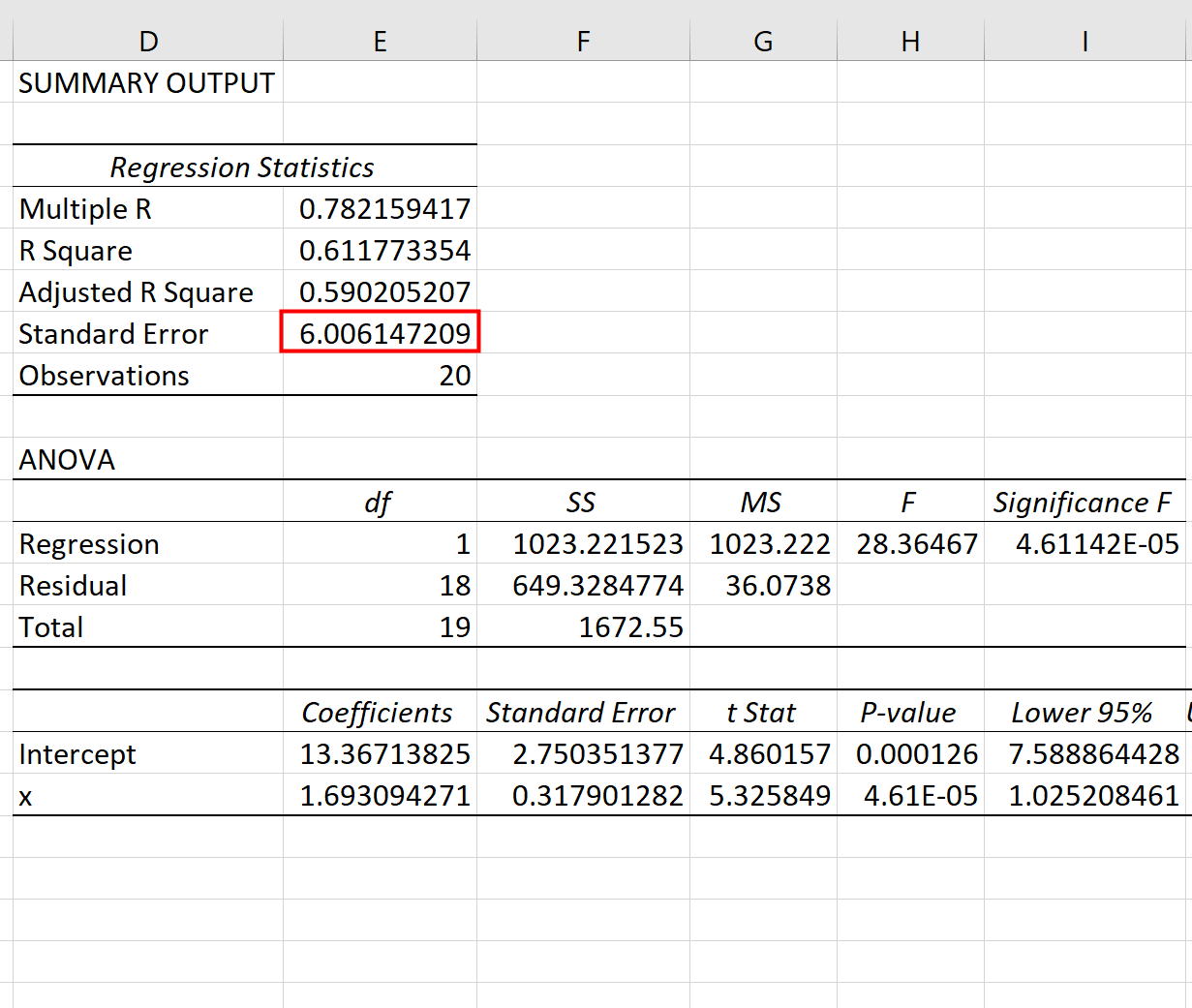
Мы можем использовать коэффициенты из таблицы регрессии для построения расчетного уравнения регрессии:
ŷ = 13,367 + 1,693(х)
И мы видим, что стандартная ошибка оценки для этой регрессионной модели оказывается равной 6,006 . Проще говоря, это говорит нам о том, что средняя точка данных находится на расстоянии 6,006 единиц от линии регрессии.
Мы можем использовать расчетное уравнение регрессии и стандартную ошибку оценки, чтобы построить 95% доверительный интервал для прогнозируемого значения определенной точки данных.
Например, предположим, что x равно 10. Используя расчетное уравнение регрессии, мы могли бы предсказать, что y будет равно:
ŷ = 13,367 + 1,693*(10) = 30,297
И мы можем получить 95% доверительный интервал для этой оценки, используя следующую формулу:
- 95% ДИ = [ŷ – 1,96*σ is , ŷ + 1,96*σ is ]
Для нашего примера 95% доверительный интервал будет рассчитываться как:
- 95% ДИ = [ŷ – 1,96*σ is , ŷ + 1,96*σ is ]
- 95% ДИ = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
- 95% ДИ = [18 525, 42 069]
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как создать остаточный график в Excel