Связь между средним и стандартным отклонением (с примером)
Среднее значение представляет собой среднее значение в наборе данных.
Он рассчитывается следующим образом:
Выборочное среднее = Σx i /n
Золото:
- Σ: Символ, означающий «сумма».
- x i : i -е наблюдение в наборе данных.
- n: общее количество наблюдений в наборе данных
Стандартное отклонение представляет собой распределение значений в наборе данных относительно среднего значения.
Он рассчитывается следующим образом:
Стандартное отклонение выборки = √ Σ(x i – x bar ) 2 / (n-1)
Золото:
- Σ: Символ, означающий «сумма».
- x i : i- е значение выборки
- x bar : Образец означает
- n: Размер выборки
Обратите внимание на взаимосвязь между средним значением и стандартным отклонением: среднее значение используется в формуле для расчета стандартного отклонения .
Фактически, мы не можем вычислить стандартное отклонение выборки, если не знаем выборочное среднее значение.
В следующем примере показано, как на практике рассчитать выборочное среднее и выборочное стандартное отклонение для набора данных.
Пример. Расчет среднего и стандартного отклонения для набора данных
Допустим, у нас есть следующий набор данных, который показывает очки, набранные 10 разными баскетболистами:
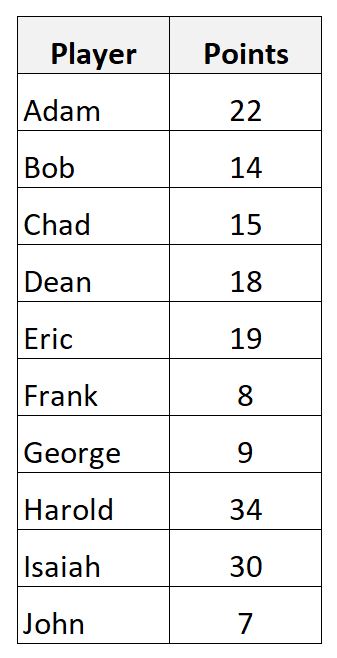Мы можем рассчитать выборочное среднее количество набранных баллов, используя следующую формулу:
- Выборочное среднее = Σx i /n
- Среднее выборочное = (22+14+15+18+19+8+9+34+30+7) / 10
- Выборочное среднее = 17,6
Среднее выборочное набранное количество баллов составляет 17,6 . Это среднее количество очков, набранных всеми игроками.
Как только мы узнаем выборочное среднее значение, мы можем подставить его в формулу для расчета выборочного стандартного отклонения:
- Стандартное отклонение выборки = √ Σ(x i – x bar ) 2 / (n-1)
- Стандартное отклонение выборки = √ ((22-17,6) 2 + (14-17,6) 2 + (15-17,6) 2 + (18-17,6) 2 + (19-17,6) 6) 2 + (8-17,6) 2 + (9-17,6) 2+ (34-17,6) 2+ (30-17,6) 2+ (7-17,6) 2 )/(10-1)
- Стандартное отклонение выборки = 9,08.
Стандартное отклонение выборки составляет 9,08 . Это представляет собой среднее расстояние между значением каждой точки и средним значением точки выборки.
Полезно знать как среднее значение, так и стандартное отклонение набора данных, поскольку каждый показатель говорит нам о чем-то своем.
Среднее значение дает нам представление о том, где находится «центральное» значение набора данных.
Стандартное отклонение дает нам представление о распределении значений вокруг среднего значения в наборе данных. Чем выше значение стандартного отклонения, тем более разбросаны значения в выборке.
Зная эти два значения, мы можем многое узнать о распределении значений в наборе данных.
Дополнительные ресурсы
Следующие учебные пособия предоставляют дополнительную информацию о среднем и стандартном отклонении:
Почему среднее значение важно в статистике?
Почему стандартное отклонение важно в статистике?
Как рассчитать среднее и стандартное отклонение в Excel
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше